[기계학습개론] Regression

SUbbb·2021년 10월 24일
기계학습개론
0

기계학습개론

목록 보기
4/10
post-thumbnail

선형회귀, 오차, Gradient Descent(경사하강법)

선형회귀 정의

독립 변수:

  • 'x값이 변함에 따라 y값도 변한다'는 정의 안에서, 독립적으로 변할 수 있는 x값

종속 변수:

  • 독립 변수에 따라 종속적으로 변하는 값

선형 회귀:

  • 독립 변수 x를 사용해 종속 변수 y의 움직임을 예측하고 설명하는 작업을 말함

단순 선형 회귀 (simple linear regression):

  • 하나의 x값으로도 y값을 설명할 수 있을 때 (1차)

다중 선형 회귀 (multiple linear regression):

  • x값이 여러 개 필요할 때

단순 선형회귀 예시

공부한 시간2시간4시간6시간8시간
성적81점93점91점97점

  • 공부한 시간을 x, 성적을 y라 할 때 집합 X와 집합 Y를 다음과 같이 표현할 수 있다.
    X={2,4,6,8}X = \{2,4,6,8\}, Y={81,93,91,97}Y=\{81,93,91,97\}
    y=ax+by = ax + b,

  • 최소 제곱법(method of least squares)
    a=(x−x평균)(y−y평균)의합(x−x평균)2의합a=\frac{(x-x평균)(y-y평균)의 합}{(x-x평균)^2의합}

위의 예시에 최소 제곱법을 적용하면, a=2.3a=2.3이 도출되고,
b=y의 평균−(x의 평균×기울기a)b=y의\,평균-(x의\,평균\times기울기a)로 b를 구하면,
최종 식은 y=2.3x+79y=2.3x + 79가 된다.(→\rarr선형모델)

오차가 발생

x가 너무 많으면?

오차수정

잘못 그은 선 바로 잡기

  • 일단 선을 그리고 조금씩 수정해 나가기
  • 오차(예측값과 실제값의 차이)가 최소가 될 때까지

임의의 선

오차 = 예측 값 - 실제 값?

단순히 오차의 Sum을 하면 0에 가까워짐.

오차

평균 제곱 오차(Mean Squared Error, MSE)

MSE=1n∑(y^i−yi)2MSE = \frac{1}{n}\sum(\hat y_i-y_i)^2

코드

  • predict(x) 에서 return 해주는 값이 y^\hat y(예측 값)

오차 수정하기

  • 기울기 a와 오차와의 관계: 적절한 기울기(예시에서는 m)를 찾았을 때 오차가 최소화됨.
  • 기울기가 +인 경우: 왼쪽으로 이동
  • 기울기가 -인 경우: 오른쪽으로 이동

경사하강법(Gradient Descent)

  • 기울기가 최소화될 수 있도록 이동하는데, 그림에서 보는 것과 같이 지그재그 방식으로 하강
  • 이 때, 이동시킬 거리를 "step"이라고 한다.

학습률(Learning Rate)

학습률

  • 어느 만큼 이동시킬지를 신중히 결정해야 하는데, 이때 이동 거리를 정해주는 것

경사하강법

  • 오차의 변화에 따라 2차 함수 그래프를 만들고 적절한 학습률을 설정해 미분 값이 0인 지점을 구하는 것
  • MSE:
    1n∑(y^i−yi)2→yi=axi+b↓1n∑((axi+b)−yi)2\frac{1}{n}\sum(\hat y_i-y_i)^2 \rarr y_i=ax_i+b \\ \darr \\ \frac{1}{n}\sum((ax_i+b)-y_i)^2
    a로 편미분한 결과 = 2n∑(axi+b−yi)xi\frac{2}{n}\sum(ax_i+b-y_i)x_i
    b로 편미분한 결과 = 2n∑(axi+b−yi)\frac{2}{n}\sum(ax_i+b-y_i)

경사하강법(코드)

  • lr(learning rate)가 클수록, Gradient 또한 증가

Using scikit-learn

  • LinearRegression을 사용하고, fit()가 학습하는 method

[심화] 선형회귀, 경사하강법

선형회귀 모델 일반화

다중선형회귀 예측모델

  • y^\hat y는 예측 값
  • nn은 특징의 수
  • xix_i는 ithi^{th} 특징 값
  • θj\theta_j는 jthj^{th} 모델 파라미터 (모델에 필요한 계수나 상수)

y^=θTx\hat y=\theta^Tx

<방정식 4.1을 벡터형태로 변환>

  • MSE 측정

  • 일반 방정식

    • θ^\hat \theta는 비용 함수를 최소화하는 θ\theta값
    • yy는 y(1)y^{(1)}부터 y(m)y^{(m)}를 포함하는 목적 값의 벡터

Gradient Descent

ML model 학습 방법의 일종

  • Gradient Descent의 일반적인 아이디어는 비용 함수를 최소화하기 위해 parameter를 반복적으로 조정하는 것
    1) 랜덤 값 θ\theta로 채우고 시작
    2) step by step으로 점진적 향상
    - 각 step은 비용 함수의 감소를 시도
    - 알고리즘이 최소로 수렴될 때까지 반복

Pitalls

  • Local minimum을 Global minimum으로 착각할 수 있는 문제
  • plateau 부분에서 평탄함으로 인해 학습이 진행되지 않음

Gradient Descent 문제 해결법1

Batch Gradient Descent

  • 모든 샘플에 대한 Gradient의 평균 계산
  • 이후 모델의 parameter를 수정

▽θMSE(θ)\triangledown_\theta MSE(\theta)는 모든 θ\theta(sample)의 평균 Gradient 계산

η\eta는 learnging rate를 의미

learning rate에 따라 기울기의 변화폭이 달라짐 (큰 범위로 이리저리 이동하게 됨(step))

Gradient Descent 문제 해결법2

Batch Gradient Descent의 단점

  • training set이 큰 경우 매우 느리다.
    • 모든 sample에 대한 평균 Gradient계산 때문

Stochastic Gradient Descent

  • Batch Gradient Descent의 단점 보완
  • 매 step마다 training set에서 random instance를 선택
  • 선택한 instance에 대해서만 gradients를 계산
    →\rarr BGD보다 훨씬 빠른 속도 (gradient의 update 속도)

  • 왼쪽이 SGD, 오른쪽이 BGD
  • SGD는 선택되는 샘플에 따라 비용 함수 최소화를 위한 경로가 좌지우지되지만, BGD는 평균 계산에 의해 안정적인 형태

  • Random 선택되는 샘플을 통해 Pitfall을 해결할 수 있다.

Gradient Descent 문제 해결법3

Mini-batch Gradient Descent

  • SGD는 비용 함수 최소점에 수렴하는 데 오래 걸릴 수가 있는 문제 존재, 또한 sample 1개에 대한 계산을 수행하기에 GPU의 성능을 모두 활용하지 않는다.
  • Mini-batch GD는 mini-batches라고 불리는 작은 random sets에 대한 기울기를 계산한다.
  • SGD와 비교하여 주된 이점:
    • 특히 GPU를 사용할 때 행렬 연산의 HW 최적화로 성능이 향상된다.

BGD, SGD, MBGD에 대한 참고자료

  • MBGD는 SGD보다는 안정적, BGD보단 random

다항회귀(Polynomial Regression), 로지스틱회귀(Logistic Regression), 활성화함수(Activation Function), 규제(Regularization)

data가 선형적이지 않고 더 복잡한 경우, linear model로 처리할 수 있는가?

Example: nonlinear data

  • Polynomial Regression으로 비선형 데이터에 대한 prediction을 수행

Polynomial Regression

  • 여러 특징들이 존재할 때, 특징 간의 관계를 찾을 수 있다.
  • 일반적인 Linear Regression model은 할 수 없는 것

High-degree Polynomial Regression

  • 일반적인 Linear Regression보다 training data를 훨씬 더 잘 fitting할 수 있다.
    • 300 degree: overfitting
    • 1 degree: underfitting

과잉적합/과소적합의 판단

Underfitting

  • (Validation set을 추가)
  • learning curves를 확인

일반적인 Linear Regression model의 underfitting 문제
RMSE가 감소하지 않고 정체됨 -> 모델에 한계가 존재함을 의미

과소적합을 판단한 경우, 어떻게 해결?

  • underfitting인 경우, training examples를 추가하는 것은 도움이 되지 않는다.(모델 자체의 문제)
  • 더 복잡한 model을 사용
  • 더 나은 특징을 사용

Overfitting

  • 10th-degree polynomial model의 learning curves

    • Underfitting의 경우와 비교하면, RMSE는 전체적으로 감소했지만 Set간의 Gap이 증가
      →\rarr Model이 Validation set을 틀림
      ⇒\Rightarrow training set에만 맞춰진 것, Overfitting

Overfitting 해결법1

Regularization

= 규제, 정규화

  • overfitting을 줄이는 좋은 방법은 model을 일반화시키는 것이다.
  • Freedom(자유도)가 적을수록 데이터를 overfitting시키기가 어려워진다.
    • 오히려 알지 못하는 data에 fitting이 쉬워질 수 있다.
    • polynomial model을 일반화하는 쉬운 방법은 polynomial degree의 수를 줄이는 것이다.
    • degree와 freedom은 비례

Ridge Regression

Linear Regression의 일반화된 버전

  • 정규화 항이 비용 함수에 추가된다.
  • l2l_2 norm을 사용 (제곱 사용)

    • α\alpha를 통해 해당 파라미터를 조정하고, α\alpha가 증가하면 기울기 변화폭이 작아진다.

Examples

  • 왼쪽: plain Ridge models
  • 오른쪽: Polynomial Regression with Ridge regularization
    • α\alpha가 증가하면, 곡선의 진폭이 감소하고 비용 자체의 증가
    • training set으로 fitting되는 경향을 막을 수는 있으나, error가 커진다.(값들과의 오차가 커짐)

Lasso Regression

Linear Regression의 일반화된 다른 버전

  • Ridge Regression이 하는 것과 같이 비용 함수에 정규화 항을 추가
  • l1l_1 norm을 사용 (절대값 사용)

Examples

plain Ridge models

  • 제곱을 사용했기 때문에 변화폭이 크다.

Polynomial Regression with Lasso regularization

  • 절대값 사용으로 변화폭이 크지 않고, 자유도가 더 있는 것처럼 보인다.

Overfitting 해결법2

model을 변경하거나 cost function을 변경하는 방법 X

  • Early Stopping
  • 앞에서 다룬 반복적인 학습 알고리즘과는 달리 검증 에러가 최소가 되는 시점에 학습을 멈추는 것

  • Validation set의 error는 기본적으로 Training set보다 크다.
  • Training set에 대해서는 epoch가 증가할수록, error는 감소한다.
  • 학습횟수(epoch)가 일정 시점 이상으로 증가하게 되면, training set에 대한 overfitting으로 인한 error가 증가하게 되고, 증가하기 직전의 시점이 Best Model이므로 Early stopping을 하는 시점이 된다.

Logistic Regression

Logistic Regression

  • 어떤 class에 속하는지 속하지 않는지 구분(분류)하는 회귀
  • binary classifier를 생성한다.
  • Linear Regression model처럼, 입력된 특징에 대한 가중합을 구하지만(bias 항 포함), 결과의 logistic을 출력한다.
  • Logistic function
    σ(t)=11+exp(−t)\sigma(t)=\frac{1}{1+exp(-t)}

  • 분모가 최소가 될 때, 함수의 값은 최대 1이 되고, 분모가 최대가 될 때, 함수의 값은 최소 0이 된다.
    • 0과 1사이의 값으로 한정 가능
  • Logistic Regression model prediction

    • 결과값을 확률로 생각할 수 있고, 0.5를 기준으로 0이냐 1이냐로 구분할 수 있다.

Logistic Regression: code

  • 파란 점선: Not iris
  • 초록 실선: Iris Virginica

Decision Boundaries

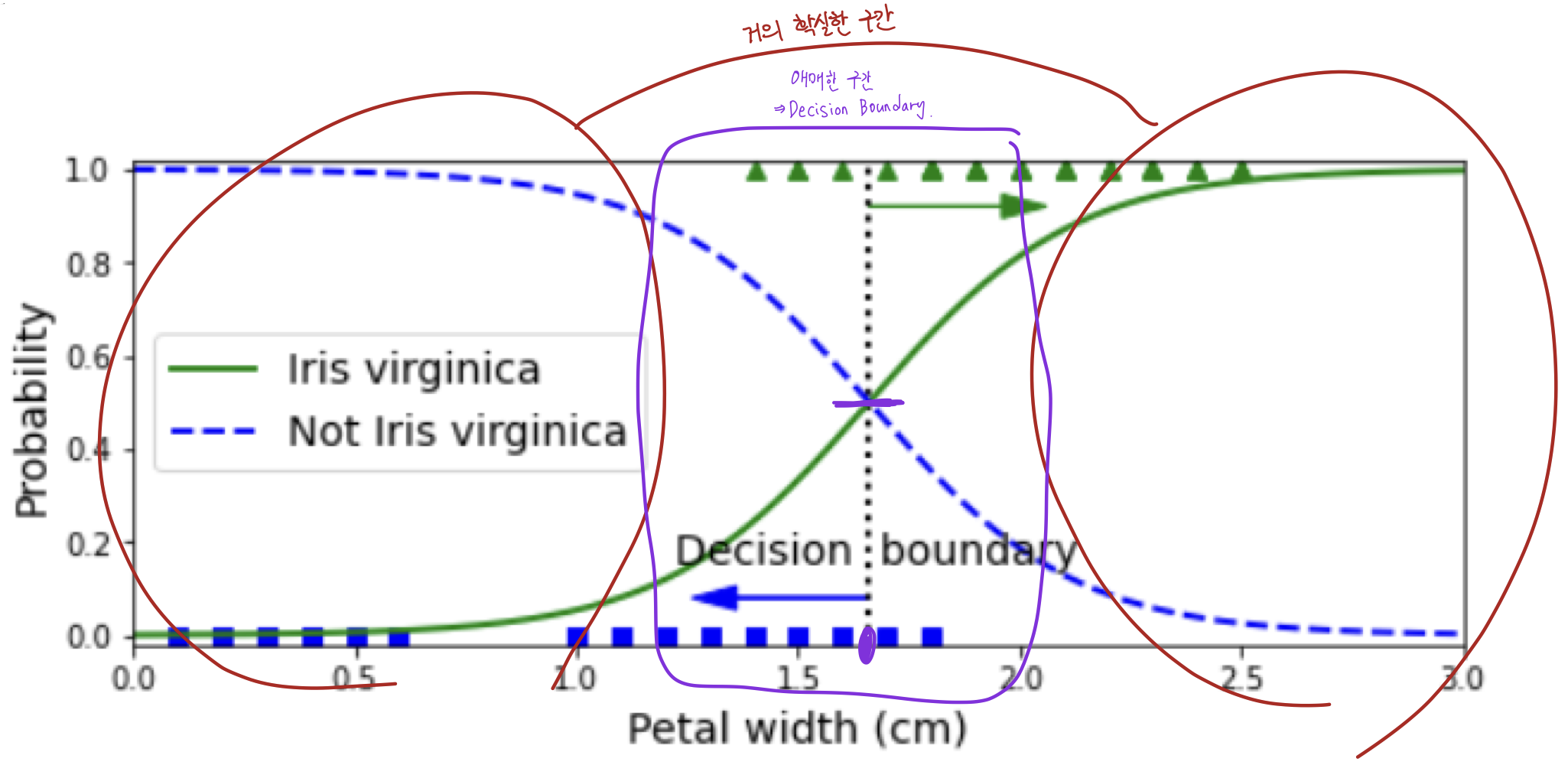
  • 보라색 구간은 결정이 애매한 구간으로, Decision Boundary

petal width & length display (2차원)

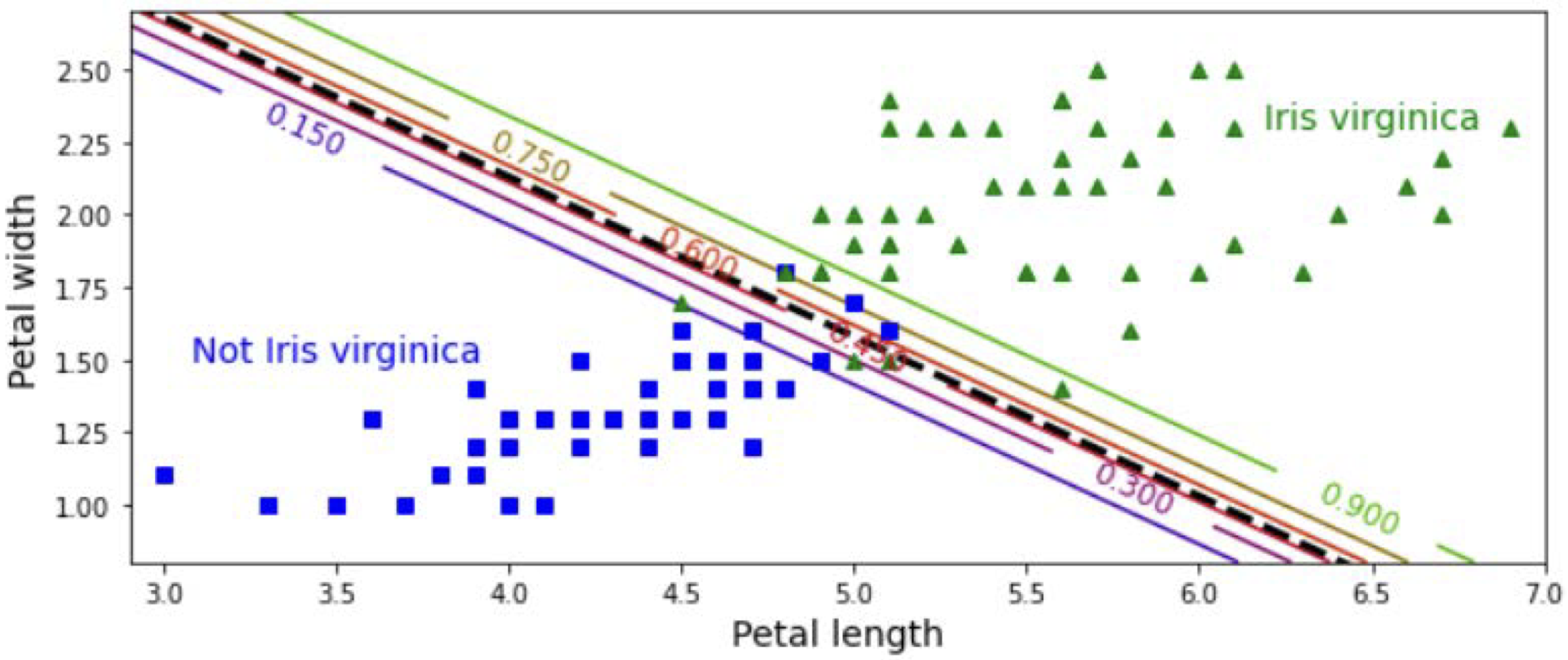
  • 선에 있는 숫자들은 Iris인가에 대한 확률값

Logistic Regression이 일반화될 수 있는가?

Softmax Regression

  • Logistic Regression model이 여러 binary classifiers를 학습하거나 결합하지 않고 여러 classes 지원을 위한 일반화가 가능하다. 즉, 하나의 model만으로 여러 가지를 분류할 수 있다.
  • 이를 Softmax Regression이라 한다.

Main idea: 각 class마다의 score를 매겨서 제일 높은 값의 class로 출력

  • 주어진 x에 대해서, Softmax Regression model은 각 class k에 대한 score sk(x)s_k(x)를 계산
  • scores에 softmax functionsoftmax\,function을 적용함으로써, 각 class의 확률을 계산
    • score값이 제일 큰 class로 분류

Cross entropy cost function

Softmax Regression 학습 시 사용

Example

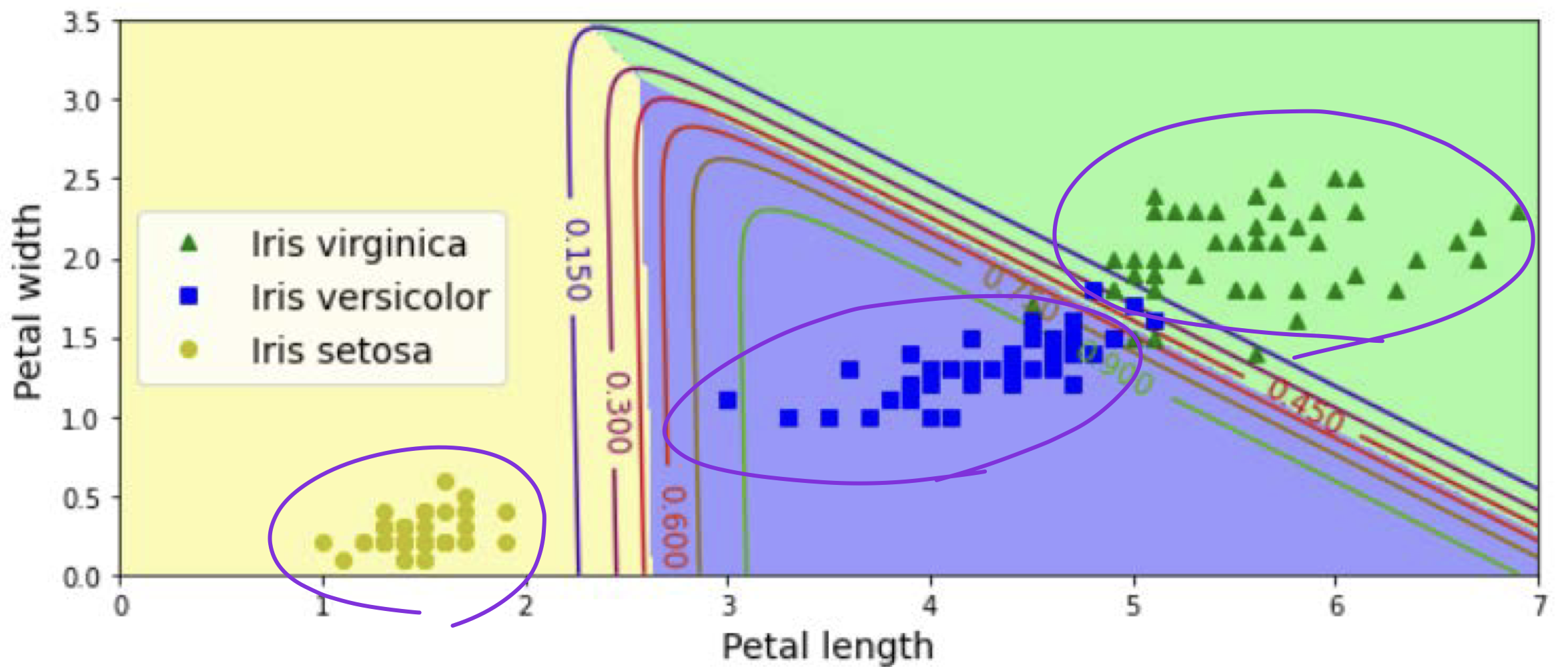
두 직선을 이용해 score를 계산하여 multiple class에 대한 분류가 가능해진다.

profile
SUbbb
배우고 정리하고 공유하기
이전 포스트

[기계학습개론] Data Processing for ML

다음 포스트

[기계학습개론] Decision Tree

0개의 댓글