TIL | 면접 카타 - 병합/삽입 정렬

병합 정렬(Merge Sort)

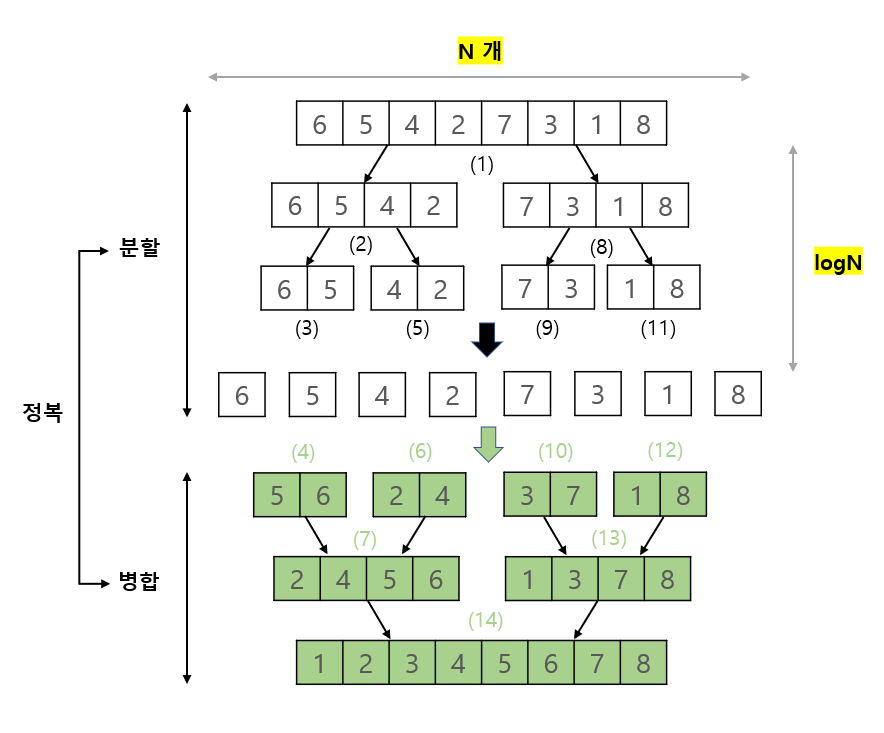
병합 정렬은 분할 정복(divide and conquer) 전략을 사용하는 정렬 방법입니다. 이 방법은 배열을 반으로 나누어 각 부분을 재귀적으로 정렬한 후, 두 부분을 합쳐 전체를 정렬하는 방식으로 작동합니다. 병합 정렬의 주요 단계는 다음과 같습니다:

1. 분할(Divide): 배열을 두 부분으로 나눕니다.
2. 정복(Conquer): 각 부분을 재귀적으로 정렬합니다.
3. 결합(Combine): 정렬된 두 배열을 합쳐서 하나의 정렬된 배열로 만듭니다.
   
   https://www.google.com/url?sa=i&url=https%3A%2F%2Fvelog.io%2F%40jimmy48%2F%25EB%25B3%2591%25ED%2595%25A9-%25EC%25A0%2595%25EB%25A0%25ACMerge-Sort&psig=AOvVaw0lR4-DUAKN6GvEWAigfnnc&ust=1712881849863000&source=images&cd=vfe&opi=89978449&ved=0CBIQjRxqFwoTCOjJn6z0uIUDFQAAAAAdAAAAABA5

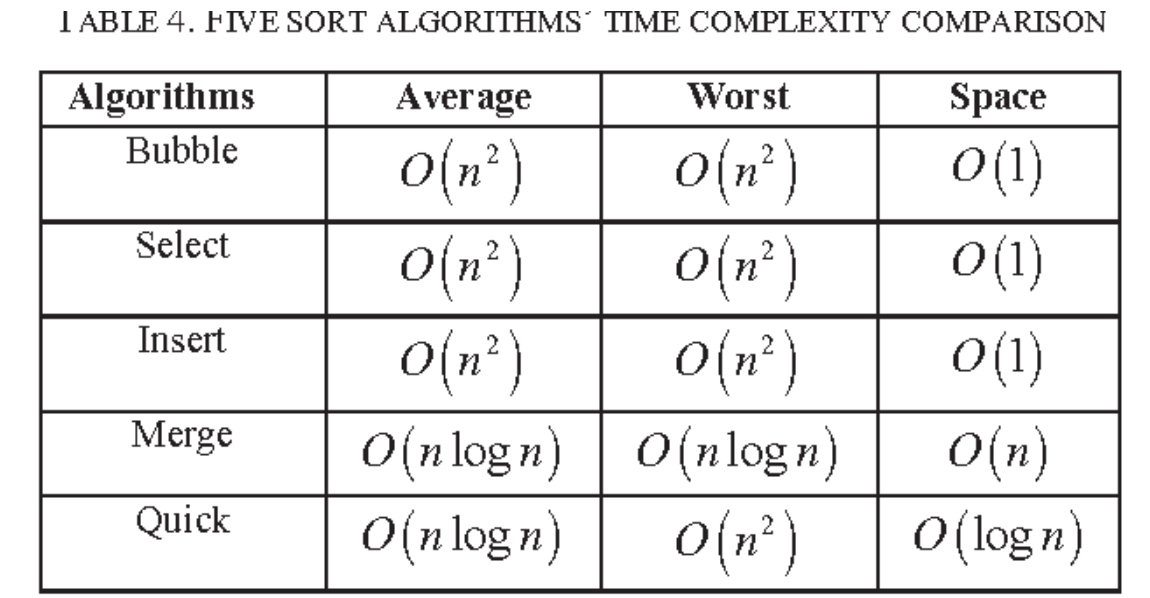
병합 정렬의 시간 복잡도는 모든 경우에 대해 (O(n \log n))입니다. 이는 병합 정렬이 데이터의 분포에 관계없이 일정한 성능을 보여준다는 것을 의미합니다. 대용량 데이터를 다룰 때 효율적이지만, 추가적인 메모리 공간이 필요한 것이 단점입니다.

function mergeSort(arr) {
    if (arr.length <= 1) {
        return arr;
    }

    const middle = Math.floor(arr.length / 2);
    const left = arr.slice(0, middle);
    const right = arr.slice(middle);

    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
    let resultArray = [], leftIndex = 0, rightIndex = 0;

    while (leftIndex < left.length && rightIndex < right.length) {
        if (left[leftIndex] < right[rightIndex]) {
            resultArray.push(left[leftIndex]);
            leftIndex++; // move left array cursor
        } else {
            resultArray.push(right[rightIndex]);
            rightIndex++; // move right array cursor
        }
    }

    // Concatenating the leftover elements
    // (in case we didn't go through the entire left or right array)
    return resultArray
        .concat(left.slice(leftIndex))
        .concat(right.slice(rightIndex));
}

삽입 정렬(Insertion Sort)

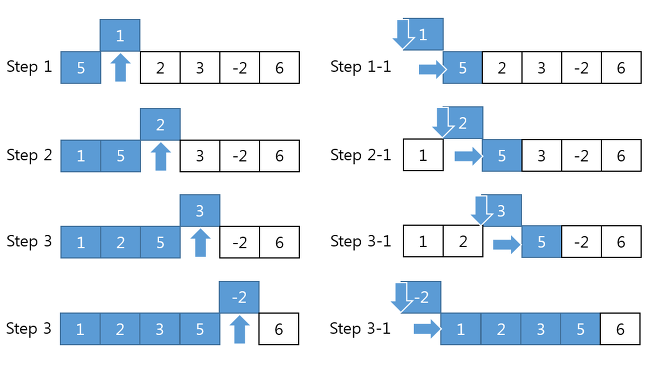
삽입 정렬은 각 반복에서 요소를 적절한 위치에 삽입하는 방식으로 배열을 정렬합니다. 배열의 모든 요소를 차례대로 이미 정렬된 배열 부분과 비교하여, 각 요소를 적절한 위치에 삽입하여 정렬을 완성합니다. 삽입 정렬의 주요 단계는 다음과 같습니다:

1. 배열의 두 번째 요소부터 시작하여, 해당 요소를 임시 변수에 저장합니다.
2. 임시 변수의 값을 이미 정렬된 배열 부분의 요소들과 비교하여, 적절한 위치에 삽입합니다.
3. 위의 과정을 배열의 모든 요소에 대해 반복합니다.
   
   https://www.google.com/url?sa=i&url=https%3A%2F%2Fmedium.com%2F%40mackertech%2Fc-%25EC%2582%25BD%25EC%259E%2585-%25EC%25A0%2595%25EB%25A0%25AC-%25EC%2595%258C%25EA%25B3%25A0%25EB%25A6%25AC%25EC%25A6%2598-5c73d3043cc0&psig=AOvVaw12A_Md4ZzMZH8GpoG_gpjP&ust=1712882481073000&source=images&cd=vfe&opi=89978449&ved=0CBIQjRxqFwoTCLjTkdX2uIUDFQAAAAAdAAAAABAE

삽입 정렬의 평균 및 최악 시간 복잡도는 (O(n^2))입니다. 하지만 이미 정렬된 데이터에 대해서는 매우 빠르게 동작하며, (O(n))의 시간 복잡도를 가집니다. 작은 데이터셋에 대해 효율적이지만, 데이터의 양이 많아질수록 성능이 급격히 떨어집니다.

function insertionSort(arr) {
    for (let i = 1; i < arr.length; i++) {
        let key = arr[i];
        let j = i - 1;

        // Move elements of arr[0..i-1], that are greater than key,
        // to one position ahead of their current position
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
    return arr;
}