99클럽 코테 스터디 3일차 TIL - Custom Bound

김용범·2025년 1월 15일

99클럽 TIL 개발자취업 코딩테스트준비 항해99

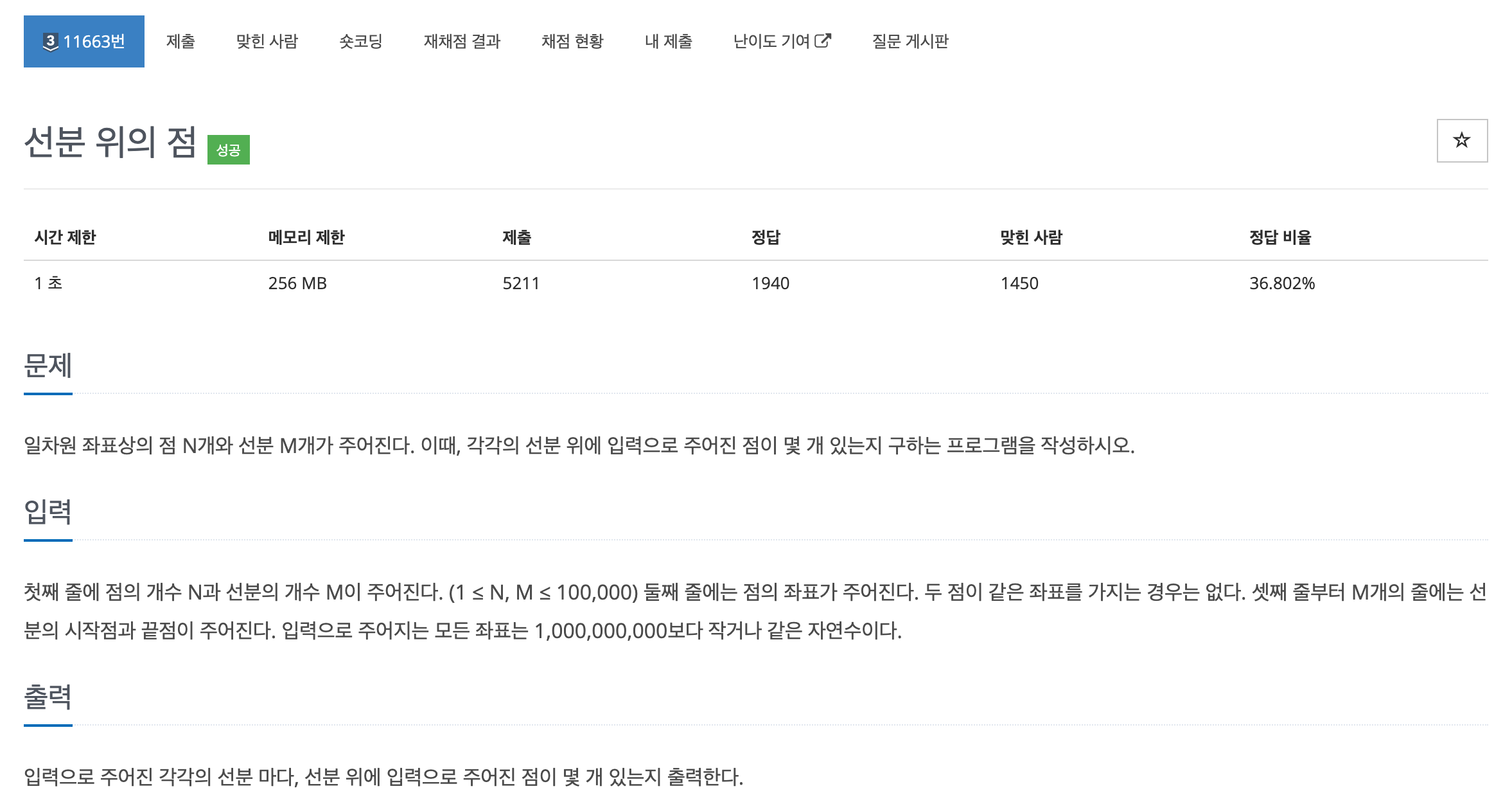
문제 💁🏻‍♂️

문제 링크 - 백준 11663 선분 위의 점

해결 과정

이 문제를 처음 보고, 접근을 잘 하지 못했다. N과 M의 범위가 크기 때문에 각 N마다 M개의 선분을 모두 탐색하는 것은 포기해야 한다는 것은 깨달았다. 문제에 접근하기 위해서 다음과 같은 사고를 했다.

사고 과정 ❗️

좌표의 범위가 매우 넓다.
시작점과 끝점이 존재하고, 경계점을 포함하여 해당 선분 내에 몇 개에 점이 있는지 알아야 한다.
즉, 범위와 관련된 문제이다.

내가 아는 정보 중 범위와 관련된 풀이 방법은 이분 탐색을 활용한 Lower Bound 와 Upper Bound 가 있었다. 또한, 값의 범위가 매우 큰 경우에는 높은 확률로 이분 탐색 문제일 수 도 있다는 사실을 알고 있었긴 했다. 이분 탐색을 사용한다면 선분의 길이가 1 ~ 1_000_000_000 으로 주어진다고 해도 대략 30번 정도로 구할 수 있으므로, 주어진 제한 시간을 충분히 통과할 것이라고 판단했다.

그러나, 이 Lower Bound, Upper Bound 코드를 구현하자니 너무 헷갈려서 조금 애를 먹었다. 그래서 이번 기회를 통해서 한번 제대로 정리해보려고 한다. 해당 내용은 아래 코드 부분에서 설명을 해보려고 한다. 자바 언어로 구현하려고 하니 너무 어려웠지만, 코드를 제출하고 정답 판정을 받고 나니 기분이 너무 좋았다 :)

코드

Lower Bound (= 하한)

Lower Bound 는 하한선 방식으로 특정 target 값 이상인 숫자의 첫 위치를 반환한다. 즉, target 값 이상의 값이 처음으로 등장하는 위치의 인덱스를 반환하는 로직이다.

public static int lowerBound() {
	int left = 0;
    int right = arr.length;
    
    while (left <= right) {
    	int mid = (left + right) / 2;
        if (target <= arr[mid]) {
        	right = mid - 1;
        } else {
        	left = mid + 1;
        }
    }
    
    return left;
}

Upper Bound (= 상한)

Upper Bound 는 상한선 방식으로 특정 target 값을 초과하는 숫자의 첫 위치를 반환한다. 즉, target 값보다 큰 숫자가 처음으로 등장하는 위치의 인덱스를 반환하는 로직이다.

public static int upperBound() {
	int left = 0;
    int right = arr.length;
    
    while (left <= right) {
    	int mid = (left + right) / 2;
        if (target < arr[mid]) {
        	right = mid - 1;
        } else {
        	left = mid + 1;
        }
    }
    
    return left;
}

정답 코드

import java.util.*;
import java.io.*;

public class Main {

    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    static StringTokenizer st;
    static int[] points;
    static int N, M, s, e; // N: 점의 개수, M: 선분의 개수

    public static void main(String[] args) throws IOException {

        st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());

        points = new int[N];
        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; i++)
            points[i] = Integer.parseInt(st.nextToken());

        Arrays.sort(points); // 이분 탐색을 위한 오름차순 정렬
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            s = Integer.parseInt(st.nextToken());
            e = Integer.parseInt(st.nextToken());
            int cnt = upperBound(e) - lowerBound(s) + 1;

            bw.write(cnt + "\n");
        }

        bw.close();
    }

    // target 값의 인덱스
    // target 값이 존재하지 않는다면 target 값보다 크면서 가장 작은 값의 인덱스 반환
    private static int upperBound(int target) {

        int left = 0;
        int right = N - 1;

        int idx = -1;
        while (left <= right) {

            int mid = (left + right) / 2;
            if (points[mid] <= target) {
                // 인덱스는 큰 값 중에서 가장 작은 값을 저장
                if (idx < mid)
                    idx = mid;
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return idx;
    }

    // target 값의 인덱스
    // target 값이 존재하지 않는다면 target 값보다 작으면서 가장 큰 값의 인덱스 반환
    private static int lowerBound(int target) {

        int left = 0;
        int right = N - 1;

        int idx = N;
        while (left <= right) {
            int mid = (left + right) / 2;

            if (target <= points[mid]) {
                if (idx > mid)
                    idx = mid;
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }

        return idx;
    }
}