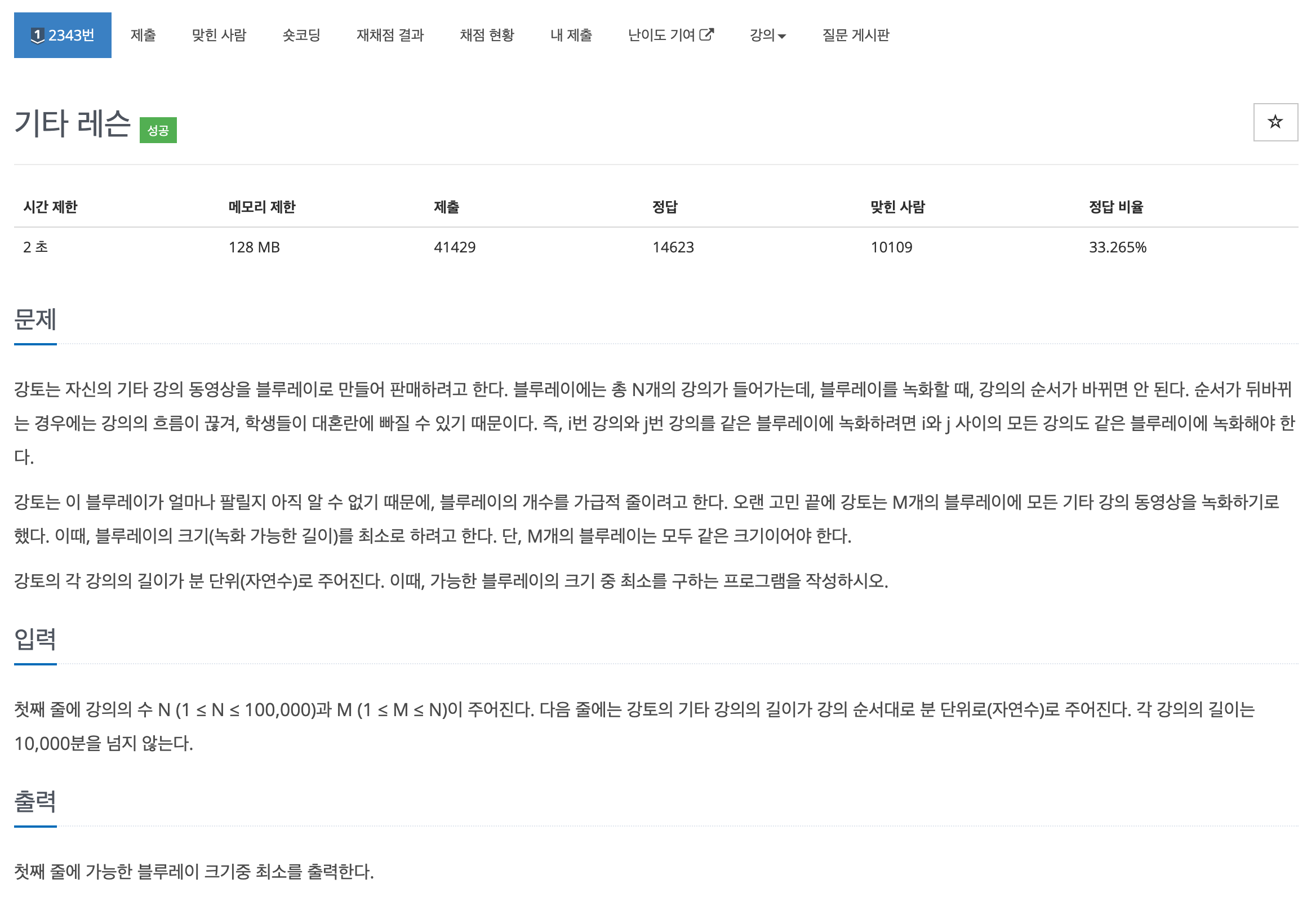
문제 💁🏻♂️
해결 과정
이 문제에 대한 고민이 많았다. 우선, 문제를 이해하는 데 시간이 조금 걸렸다. 글자가 튕기는 것을 보니 독해력이 부족하다는 생각도 들었다. 문제를 10분 정도 계속 반복해서 읽으면서 문제를 이해했고, 문제가 무엇을 요구하고 있는지 알았다. 이렇게 뭔가 어떤 요구사항을 주고, 그 기준에 맞춰서 최댓값 또는 최솟값을 구하라는 문제 유형이 바로 이분탐색을 활용한 파라메트릭 서치 이다.
사고 과정 ❗️
파라메트릭 서치 란, 쉽게 말하면 최적화 문제를 결정 문제로 바꾸어 푸는 것을 뜻한다. 즉, 문제의 상황을 만족하는 상황에서 최솟값, 최댓값을 구하는 문제이다. 이 문제를 예로 들어보면 다음과 같다.
- 상황 조건: M개 의 블루레이에 모든 기타 강의 동영상을 녹화한다.
- 개수 조건: M개 의 블루레이에 담기 위한 가능한 블루레이 크기 중 최솟값을 구해라.
- 추가 조건: i번 강의와 j번 강의를 넣고 싶다면, 그 사이에 있는 모든 강의도 넣어야 한다.
위 3가지 조건을 만족하여 코드를 구현하고, 이분탐색을 활용하여 개수 조건을 만족하는 여러 값들 중 최솟값을 구하면 된다. 단순 이분탐색이 아니라, 문제 상황에 맞게 이분탐색 코드를 커스텀하거나, 특정 알고리즘을 추가적으로 적용해야 하는 경우가 있다.
이 문제에서는 N개의 강의를 순서대로 유지해야한다는 점에서 정렬 과정이 필요한 이분탐색이 아닐 것이라고 판단하도록 유혹하고 있다. 이 점을 해석하는 것이 바로 파라메트릭 서치 문제 해결의 핵심이다. 고려해야할 점은 다음과 같다.
- 이분탐색의 left, right 값을 어떻게 설정할 것인가?
- 어느 상황일 때, 정답값을 지속적으로 갱신할 것인가? (lower냐, upper냐, custom이냐)
위 2가지 조건를 정확하고, 빠르게 판단하고 작성하기 위해서는 이분탐색 로직을 확실하게 알고 있어야한다. 나 또한, 이 문제와 알맞는 이분탐색 코드를 직접 구현하면서 여러 실수를 하느라 시간을 많이 지체했다. 그럼에도 불구하고 집중해서 코드를 구현했고, 제출하니 한번에 정답 판정을 받았다!

코드
정답 코드
import java.util.*;
import java.io.*;
public class Main_1 {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer st;
static int N, M, MAX = 0, MIN = -1; // N: 강의의 개수, M: 녹화할 블루레이의 개수
static int[] arr;
public static void main(String[] args) throws IOException {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
arr = new int[N];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
MAX += arr[i];
MIN = Math.max(MIN, arr[i]);
}
System.out.println(bs());
}
private static int bs() {
int left = MIN;
int right = MAX;
int ans = Integer.MAX_VALUE;
while (left <= right) {
int sum = 0;
int cnt = 0;
int mid = (left + right) / 2;
for (int i = 0; i < N; i++) {
if (sum + arr[i] <= mid) {
if (i == N - 1)
cnt++;
sum += arr[i];
} else {
cnt++;
sum = arr[i];
if (i == N - 1)
cnt++;
}
}
// 목표 개수와 같거나 적게 나오는 경우 -> 블루레이 크기를 줄인다.
if (cnt <= M) {
ans = Math.min(ans, mid);
right = mid - 1;
// 목표 개수보다 더 많이 나오는 경우 -> 블루레이 크기를 늘린다.
} else {
left = mid + 1;
}
}
return ans;
}
}

