문제 💁🏻♂️
해결 과정
처음 풀어보는 플래티넘 등급 문제이자, 정답률이 22.5%로 매우 낮은 문제이다. 문제를 읽어보면 그래프 문제라는 것을 바로 파악할 수 있는 힌트들이 많다.
- 서울에서 포천까지 최소 시간으로 가야한다는 것
- 두 도시(= 노드)들을 양방향으로 연결해야한다는 것
사고 과정 (1) ❗️
이 문제를 풀기 위해서 가중치가 일정하지 않다 라는 점에서 다익스트라 알고리즘을 먼저 떠올렸다. 심지어 1번 노드가 서울, N번 노드가 포천으로 출발점과 도착점이 모두 주어졌다. 다익스트라 알고리즘으로 가닥을 잡고, 도로를 K개 이하로 포장하여 최소 거리를 어떻게 구해야 할 지에 대해서 곰곰히 생각했다. 처음 떠올린 생각은 다음과 같다.
- 다익스트라 알고리즘으로 구한 최단 거리의 경로를 역추적한다.
- 역추적한 거리에서 시간이 오래걸리는 순서대로 k개의 도로를 포장하여 시간 가중치를 0으로 만든다.
- 최소 시간을 출력한다.
바로 코드를 작성해보았다. 그러나, 예제에서도 작성한 코드가 원하는 정답을 내놓지 않았다. 그 이유는 생각을 깊게 하지 않아서 생긴 문제였다. 다음 그림을 보자.
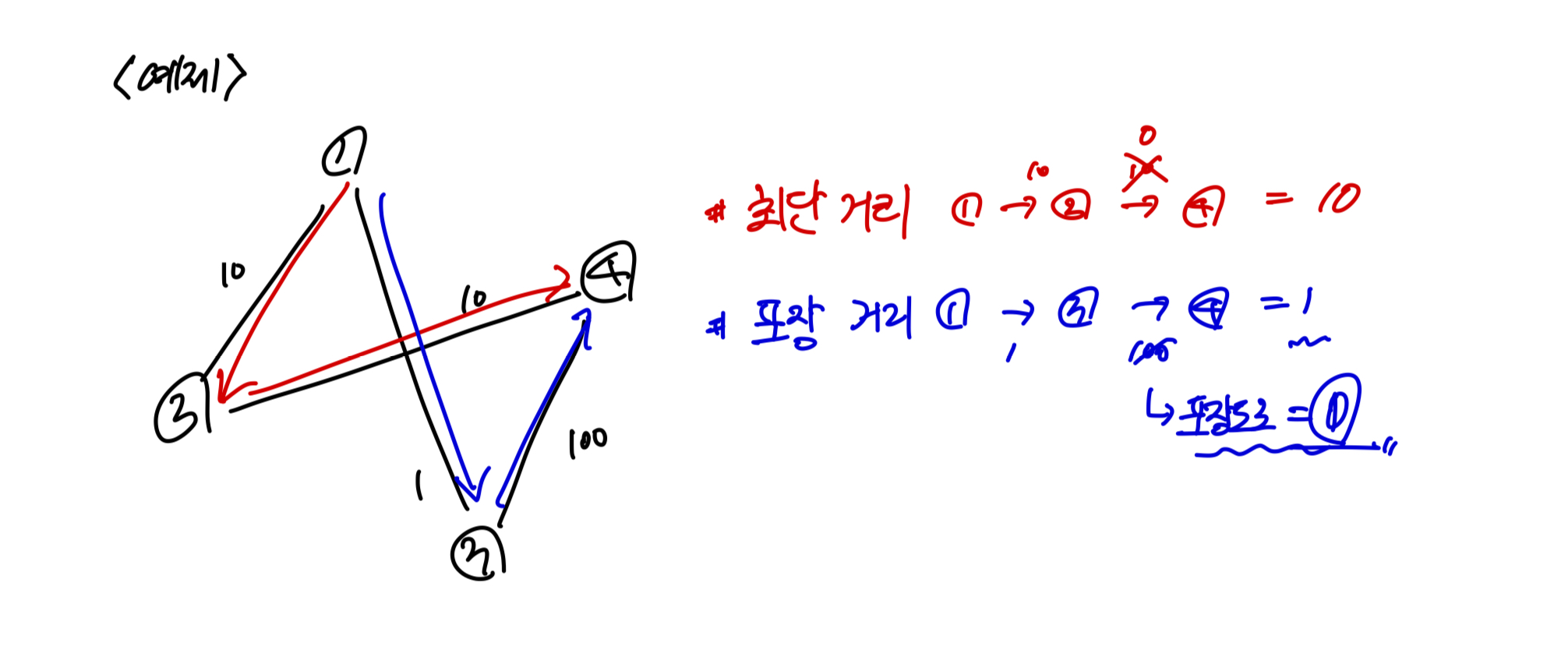
나는 다익스트로 알고리즘을 통해서 최단 거리가 보장이 되고, 그 거리 중에서 가장 큰 간선의 가중치를 0으로 만들면 역시나 최단 거리가 보장될 것이라고 생각했다. 그러나, 위 그림과 같이 간선의 가중치를 0으로 만드는 것과 최단 거리가 유지되는 것은 완전히 상관이 없는 문제였다.
사고 과정 (2) ‼️
그럼 k개 이하로 포장하여 최단 거리를 만들어야 한다는 조건을 어떻게 해석하면 좋을까? 문제를 읽어보면 반드시 k개를 사용해야 하는 것이 아니다. 그저 k개 이하로 도로를 포장하여 가중치를 0으로 만들었을 때, 최단 거리를 찾는 것이다. 20분 정도 생각해보았지만, 마땅한 해답을 찾지 못하여 정답이 서술된 블로그를 보고 공부했다. 풀이는 다익스트라 + DP 이였고, 마치 0-1 BFS 와 비슷한 로직의 풀이인 것 같기도 하고, [ 벽 부수고 이동하기 ]와 같이 차원을 하나 더 만들어 도로를 몇 개 포장했는지 저장하면서 풀이하는 것과도 닮아있었다.
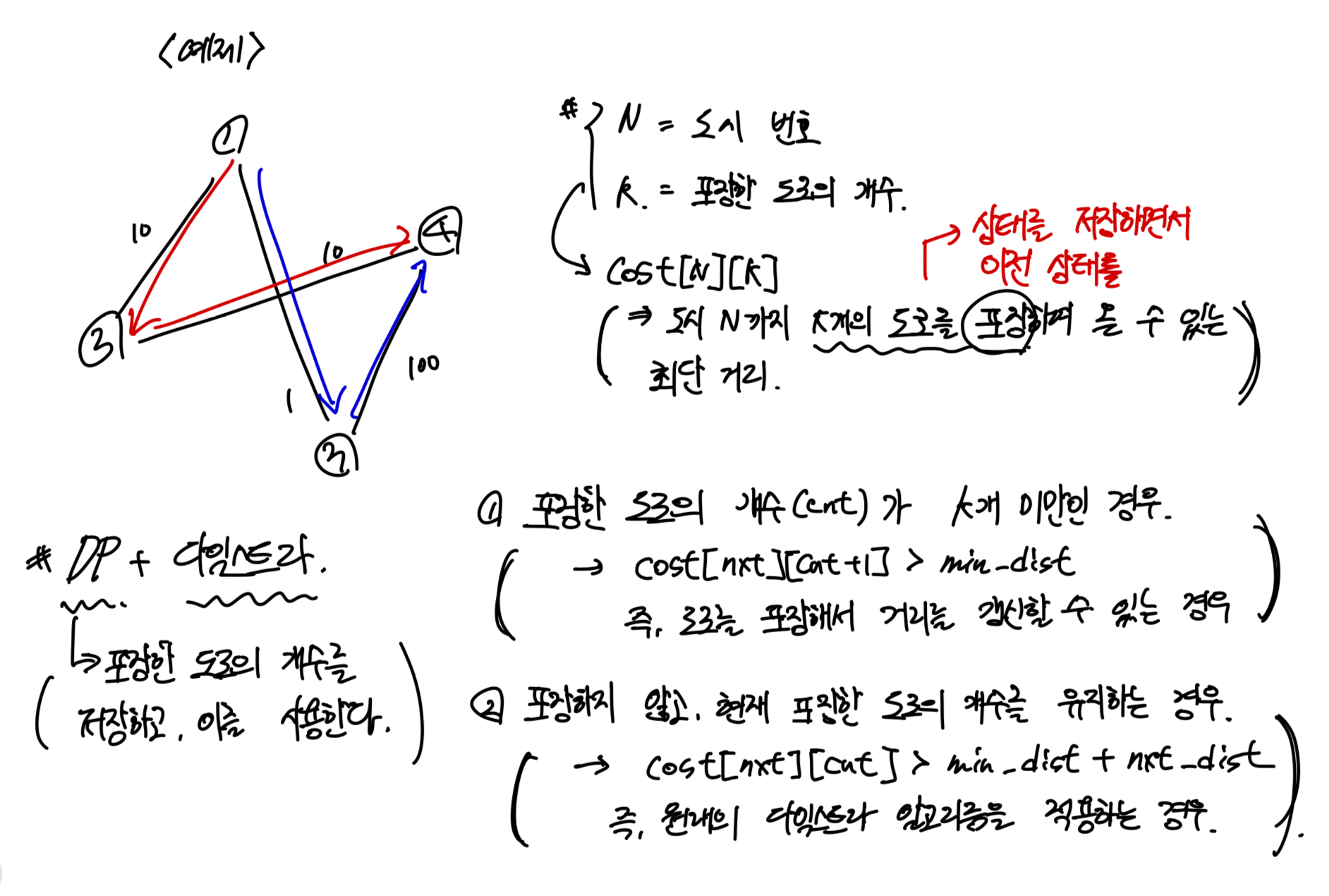
위 그림과 같이 다익스트라를 응용하여 문제를 풀이해보자.
- 다익스트라 알고리즘을 작성한다.
- 각 도시마다 주어진 포장할 수 있는 도로의 개수 k개 만큼의 공간을 만든다.
- 우선순위 큐에는 (시작 정점, 0, 포장한 도로의 개수) 를 넣어준다.
3-1. 초기값은 (1, 0, 0) 이 된다. - 포장할 수 도로의 개수가 남아있다 해도, 포장하지 않고 넘어갈 수 있다. 즉, 포장하지 않은 경우와 포장할 수 있다면 도로를 포장한 경우 모두 진행한다.
- 이 과정을 우선순위 큐가 빈 상태가 될 때까지 진행한다.
- cost[n][k] 값은 n도시까지 k개의 도로를 포장하여 얻을 수 있는 최단 거리이다. 즉, 다익스트라 알고리즘을 모두 완료한 상태에서 cost[n][0] ~ cost[n][k] 까지의 값 중에서 가장 작은 값이 이 문제가 원하는 정답이 된다.
이렇게 코드를 작성하니 문제를 해결할 수 있었다. 시간이 지난 뒤에 다시 풀어보도록 하자!

코드
정답 코드
from sys import stdin
from heapq import heappush, heappop
input = stdin.readline
def dijkstra(s, e):
INF = float('inf')
cost = [[INF for _ in range(k + 1)] for _ in range(n + 1)]
cost[s][0] = 0
pq = [(0, s, 0)]
while pq:
min_dist, cur_v, cnt = heappop(pq)
if min_dist != cost[cur_v][cnt]:
continue
for nxt_v, nxt_dist in vertex[cur_v].items():
# 포장할 수 있는 횟수가 남은 경우 -> 이동 비용 0으로 이동
if cnt < k:
# 거리를 갱신할 수 있는 경우 -> 갱신 및 heappush
if cost[nxt_v][cnt + 1] > min_dist:
cost[nxt_v][cnt + 1] = min_dist # 이동 비용: 0
heappush(pq, (min_dist, nxt_v, cnt + 1))
# 포장하지 않는 경우 -> 거리를 갱신할 수 있으면 갱신 및 heappush
new_dist = min_dist + nxt_dist
if new_dist < cost[nxt_v][cnt]:
cost[nxt_v][cnt] = new_dist
heappush(pq, (new_dist, nxt_v, cnt))
return min(cost[e][1:])
n, m, k = map(int, input().split()) # n: 도시의 수, m: 도로의 수, k: 포장할 도로의 수
vertex = [{} for _ in range(n + 1)]
# 서울: 1, 포천: n
for _ in range(m):
v1, v2, t = map(int, input().split())
if v2 not in vertex[v1]:
vertex[v1][v2] = t
vertex[v2][v1] = t
# 노드 사이에 여러 개의 도로가 입력된다면 -> 더 적은 시간을 가진 도로로 갱신
else:
vertex[v1][v2] = min(vertex[v1][v2], t)
vertex[v2][v1] = min(vertex[v2][v1], t)
dist = dijkstra(1, n)
print(dist)