문제 💁🏻♂️
해결 과정
이 문제를 읽자마자 들었던 생각은 BackTracking(= 백트래킹) 완전탐색 방법이다.
사고 과정(1) ❗️
백트래킹으로 방향성을 잡은 이유는 조건으로 주어진 N의 범위가 1 ≤ N ≤ 20 으로 작기 때문이다. 즉, O(2^20) = 10^6 정도이기 때문에 백트래킹으로 문제를 풀어도 충분하다는 판단을 내렸다. 백트래킹 문제를 연습하기 위해서 백준 N과 M 시리즈 를 추천드립니다. 해당 문제를 풀기 위한 백트래킹 조건은 다음과 같습니다.
- 인덱스 중복을 허용하지 않는다.
- 인덱스의 순서가 오름차순인 것만 경우의 수로 허용한다. 즉, 숫자 1, 2, 3, 4로 이루어진 조합은 (1, 2, 3, 4) 만 허용하며, 그 외의 조합 (4, 3, 2, 1), (4, 2, 3, 1) 등은 허용하지 않는다.
- 남은 체력이 양수(> 0)인 경우에만 유망하다고 판단하여 다음 재귀를 허용한다.
위 2가지 조건을 만족시키기 위해서 필요한 것은 visited 배열과 인덱스를 담을 리스트 가 필요하다. 이렇게 백트래킹을 정확하게 구현하면 완전탐색이기 때문에 정답을 도출할 수 있다.
사고 과정(2) ‼️
정답을 맞추고 나서 사용된 알고리즘 분류를 보니, 브루트포스 방법 외에도 DP, 배낭 문제 라는 유형이 있었다. 이 문제가 왜 DP와 배낭 문제 유형에 포함되는지 궁금했다. 우선, 배낭 문제라는 유형의 문제는 처음 접해봤기 때문에 여러 블로그를 통해서 공부했다.
배낭 문제 는 무게와 가치가 있는 여러 물건들을 무게 제한이 있는 하나의 배낭 속에 가장 높은 가치를 만들 수 있게끔 물건들을 배치하는 문제이다. 또한, 물건들을 자를 수 있는 Fractional Knapsack 문제와 물건들을 자를 수 없다고 가정하는 0-1 Knapsack 문제로 분류된다. 이번 포스팅에서 다룬 문제는 그 중에서도 0-1 Knapsack 문제였다. 점화식 내용은 명확했다.
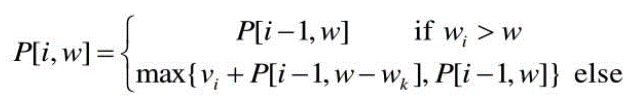
해석해보자면, i개의 다양한 물건들이 있고, 특정 i번째 물건을 배낭의 무게 제한 때문에 넣을 수 없다면 i - 1번째 물건까지 담았을 때의 최댓값을 그대로 가져온다. 반대로 특정 i번째 물건을 무게 제한 w인 배낭에 넣을 수 있다면, (i - 1번째 보석까지 담았을 때의 최댓값)과 (i번째 물건의 가치 + w - i 무게를 담았을 때의 최대 가치)를 비교하여 큰 값을 넣어준다.
즉, i - 1번째 물건까지 넣었을 때의 상태를 계속 활용하면서 최적해를 찾아가기 때문에 DP 문제로 분류되는 것이었다.
https://www.youtube.com/watch?v=S-7YAuT9nDk
처음에 이해하기가 어려웠지만, 위 링크 영상을 보며 이해할 수 있었다. 그렇게 점화식을 적용하여 문제를 풀었더니 백트래킹으로 풀었을 때의 시간보다 더욱 짧은 시간으로 문제를 해결할 수 있었다! 해당 문제를 제대로 다룬 문제는 다음 문제를 같이 풀어보면 좋을 것 같다.
코드
정답 코드 (BackTracking)
- Java Version
import java.util.*;
import java.io.*;
class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer st;
static int N, power = 100, happiness = 0, ans = 0;
static boolean[] visited;
static ArrayList<Integer> lst = new ArrayList<>();
static int[] L;
static int[] J;
public static void main(String[] args) throws IOException {
N = Integer.parseInt(br.readLine()); // N: 사람 수
L = new int[N];
J = new int[N];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++)
L[i] = Integer.parseInt(st.nextToken()); // 잃는 체력
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++)
J[j] = Integer.parseInt(st.nextToken()); // 얻는 기쁨
visited = new boolean[N];
bt(lst, 0);
System.out.println(ans);
}
private static void bt(ArrayList<Integer> lst, int total) {
ans = Math.max(ans, total);
for (int i = 0; i < N; i++) {
if (!lst.isEmpty() && lst.get(lst.size() - 1) >= i)
continue;
if (!visited[i] && power - L[i] > 0) {
visited[i] = true; // 방문 처리
lst.add(i);
power -= L[i];
bt(lst, total + J[i]);
power += L[i];
lst.remove(lst.size() - 1);
visited[i] = false; // 복원 처리
}
}
}
}- Python Version
from sys import stdin
input = stdin.readline
def bt(happiness, power, lst):
global MAX
MAX = max(MAX, happiness)
for i in range(n):
# 원소가 존재하면서, 마지막 값보다 현재 i값이 더 작다면 내림차순이므로 유망하지 않음 -> continue
if lst and lst[-1] > i:
continue
# 방문이 가능하고, power가 0보다 큰 경우 -> 유망하므로 backtracking 진행
if not visited[i] and power - L[i] > 0:
visited[i] = True # 방문 처리
lst.append(i)
bt(happiness + J[i], power - L[i], lst)
lst.pop()
visited[i] = False # 복원 처리
return
n = int(input().rstrip()) # n: 사람 수
L = list(map(int, input().split())) # L: 잃는 체력 리스트
J = list(map(int, input().split())) # J: 기쁨 점수 리스트
power = 100
happiness = 0
MAX = 0
visited = [False for _ in range(n)]
bt(0, 100, [])
print(MAX)
정답 코드 (DP - Knapsack)
import java.util.*;
import java.io.*;
class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer st;
static int N;
static int[] L;
static int[] J;
static int[][] dp;
public static void main(String[] args) throws IOException {
N = Integer.parseInt(br.readLine());
L = new int[N + 1];
J = new int[N + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++)
L[i] = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++)
J[i] = Integer.parseInt(st.nextToken());
dp = new int[N + 1][101];
for (int i = 1; i <= N; i++) {
for (int j = 1; j < 100; j++) {
int weight = L[i];
int value = J[i];
if (j < weight)
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight] + value);
}
}
System.out.println(dp[N][99]);
}
}Reference
- https://www.youtube.com/watch?v=S-7YAuT9nDk
- https://sangminlog.tistory.com/entry/boj-1535
- https://gsmesie692.tistory.com/113?category=523232
