[백준 15990] 1, 2, 3 더하기 5 (Python)

김용범·2024년 12월 26일

문제 💁🏻‍♂️

해결 과정

이 문제는 시리즈가 있는 문제이다. 1, 2, 3 더하기 시리즈 중에서도 5번째 문제로 기본 타입의 문제에서 크리티컬한 조건들이 추가된 문제이다. 숫자 1, 2, 3을 사용해서 특정 숫자를 표현해야 하는데 다음과 같은 조건이 붙었다.

합을 나타낼 때는 수를 1개 이상 사용해야 한다.
같은 수를 두 번 이상 연속해서 사용하면 안 된다.
방법의 수를 1_000_000_009로 나눈 나머지를 출력한다.

사고 과정 (1) ❗️

이 문제를 풀기 위해서 먼저 떠오른 생각은 Back Tracking(백 트래킹) 알고리즘이다. 그 이유는 바로 이전 값에 어떤 값을 더했는지 파악할 수 있어 같은 수를 2번 이상 연속해서 사용하면 안 된다. 라는 조건을 충족할 수 있을 거라고 생각했다. 그러나, n의 범위가 1 ≤ n ≤ 100_000 이기 때문에 절대 재귀로 작동하는 백트래킹으로 문제를 통과할 수 없다. 특정 조건과 합을 나타내야하는 조건 때문에 시간복잡도 측정이 어렵긴 하지만, 2^30 만 생각해도 자그마치 2^30 = 1_073_741_824 10억이 넘어 시간 초과가 난다. 그래서 다른 방법을 찾아야한다.

사고 과정 (2) ‼️

그래서 생각난 방법이 이전에 어떤 값을 더했는지 알아야 연속해서 2번 같은 수를 사용하지 않을 수 있는데, 이걸 어떻게 해결하면 좋을 지 곰곰히 생각했다. 이전 값에 따라 현재의 경우의 수가 달라진다. 라는 점에서 dp 2차원 리스트를 생각해냈다. 점화식은 다음과 같다 .

dp[i][j] = 숫자 i를 만들기 위한 방법 중 마지막 더한 숫자가 j인 경우의 수 
dp[i][1] = (dp[i - 1][2] + dp[i - 1][3]) % MOD  
dp[i][2] = (dp[i - 2][1] + dp[i - 2][3]) % MOD
dp[i][3] = (dp[i - 3][1] + dp[i - 3][2]) % MOD

이 점화식을 보자. 문제에서 주어진 예제 4를 가지고 그림으로 나타내면 다음과 같다.

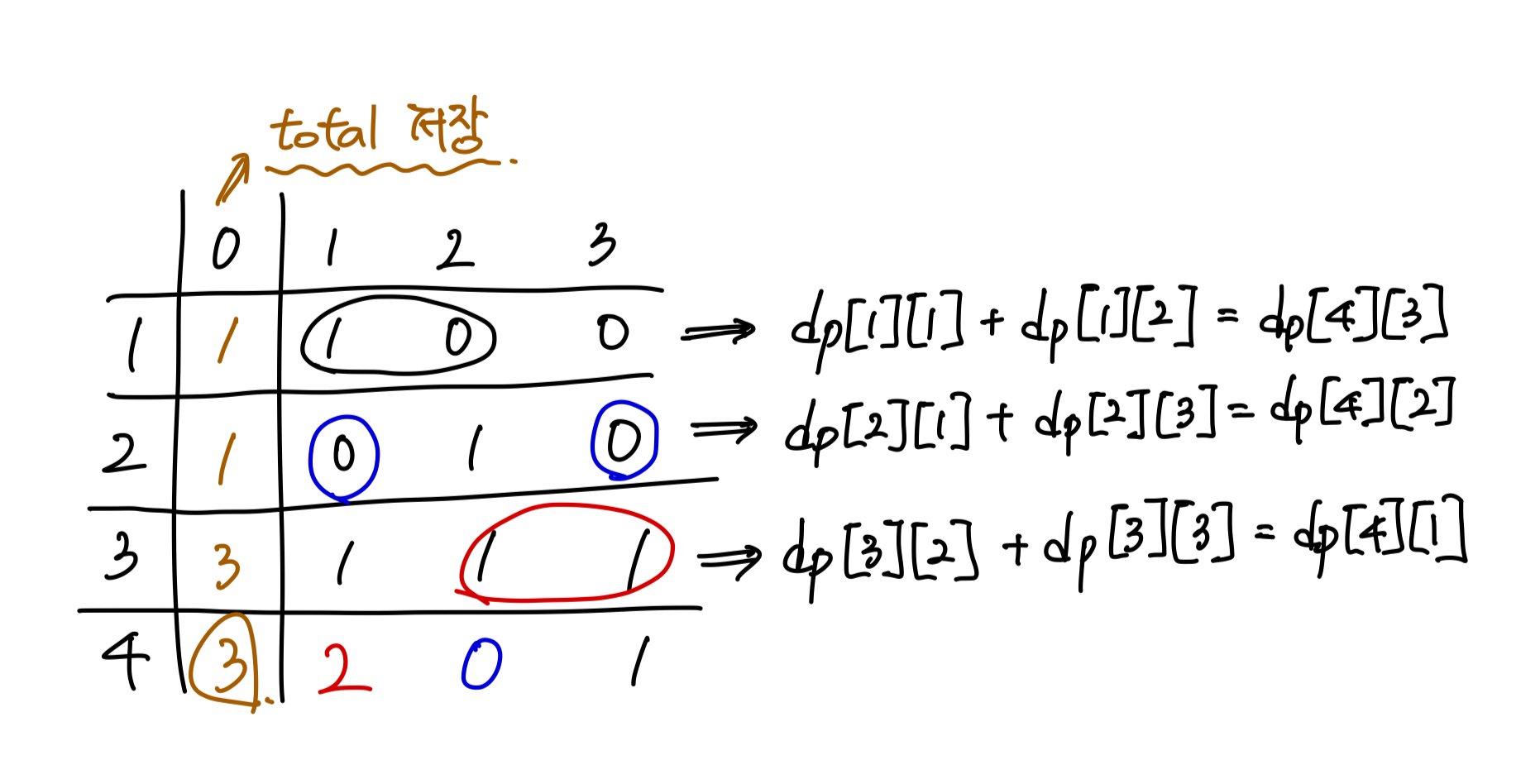
현재의 값 i 에서 3 작은 수에 대해서 3을 더해야 현재의 값 i가 되는데, 마지막 더한 숫자가 dp[i - 3][3]인 경우를 제외한 나머지 경우 즉, ... + 1 + 3 , ... + 2 + 3 과 같은 경우를 모두 더하면 dp[i][3] 즉, 마지막에 3을 더하여 현재의 i가 된 경우의 수가 되는 것이다. 이때, 문제의 조건에 따라 MOD값 = 1_000_000_009로 나눈 나머지를 저장한다. 나머지를 저장했다고 해도 모든 경우의 수를 다 더한 경우 다시 MOD를 뛰어넘을 수 있으므로 다시 한번 MOD 값으로 나눈 나머지를 정답값으로 반환한다. 이와 같이 코드를 짜고, 제출하니 정답 판정을 받았다!

코드

정답 코드

from sys import stdin

input = stdin.readline

LEN = 100_000
MOD = 1_000_000_009
# dp[i][j] -> 숫자 i를 만들기 위한 방법 중 마지막 더한 숫자가 j인 경우의 수
dp = [[0] * 4 for _ in range(LEN + 1)]
# i == 1 인 경우
dp[1][1] = 1
# i == 2 인 경우
dp[2][2] = 1
# i == 3 인 경우
dp[3][1], dp[3][2], dp[3][3] = 1, 1, 1

for i in range(4, LEN + 1):
    dp[i][3] = (dp[i - 3][1] + dp[i - 3][2]) % MOD
    dp[i][2] = (dp[i - 2][1] + dp[i - 2][3]) % MOD
    dp[i][1] = (dp[i - 1][2] + dp[i - 1][3]) % MOD

t = int(input().rstrip())
for _ in range(t):
    n = int(input().rstrip())
    print(sum(dp[n]) % MOD)