[백준 2211] 네트워크 복구 (Python)

김용범·2024년 12월 26일

문제 💁🏻‍♂️

해결 과정

이 문제는 지문의 길이가 길지만, 읽어보면 되게 간단한 문제였다. 결국 두 노드가 양방향으로 연결되어있고, 1번 노드를 시작 정점으로 설정한 후에 다음 조건을 만족하면 된다.

서로 다른 두 컴퓨터 간에 통신이 가능해야한다. 즉, 1번 노드를 시작으로 모든 정점과 연결되어있어야 한다.
1번 노드에서 시작하여 다른 모든 노드로 최단 거리로 연결되어있어야 한다.

사고 과정 (1) ❗️

나는 처음 이 문제를 읽자마자 가장 먼저 MST(최소 스패닝 트리) 알고리즘 이 떠올랐다. 그 이유는 일단 모든 노드가 연결되어 있어야 하고, 각 노드들끼리 최단 거리로 연결되어있어야 한다고 생각했기 때문이다. MST 알고리즘 중에서 union-find 을 적용하여 풀이하는 Kruskal 알고리즘으로 풀이를 진행했다. 예제에 대한 답이 잘 출력되는 것을 확인하고, 제출했다. 매우 빠른 속도로 틀렸다.

이유를 확인해봐도 알 수가 없었다. 완벽한 Kruskal 구현이었기 때문이다. 질문 게시판을 확인해보니 나와 같은 생각한 사람들이 많이 있었다. 이유를 확인해보니 내가 MST 개념과 최단 거리 개념을 알지 못하고 있음을 확인했다.

MST(최소 스패닝 트리) 알고리즘은 모든 노드가 연결되면서 그 간선의 합이 최소가 되게 하는 알고리즘이다.
Dijkstra(다익스트라) 알고리즘은 한 노드로부터 다른 노드까지 갈 수 있는 최단 거리를 구하는 알고리즘이다.

=> 즉, 두 알고리즘은 비슷한 뉘앙스를 가지지만, 서로 연관이 없다.

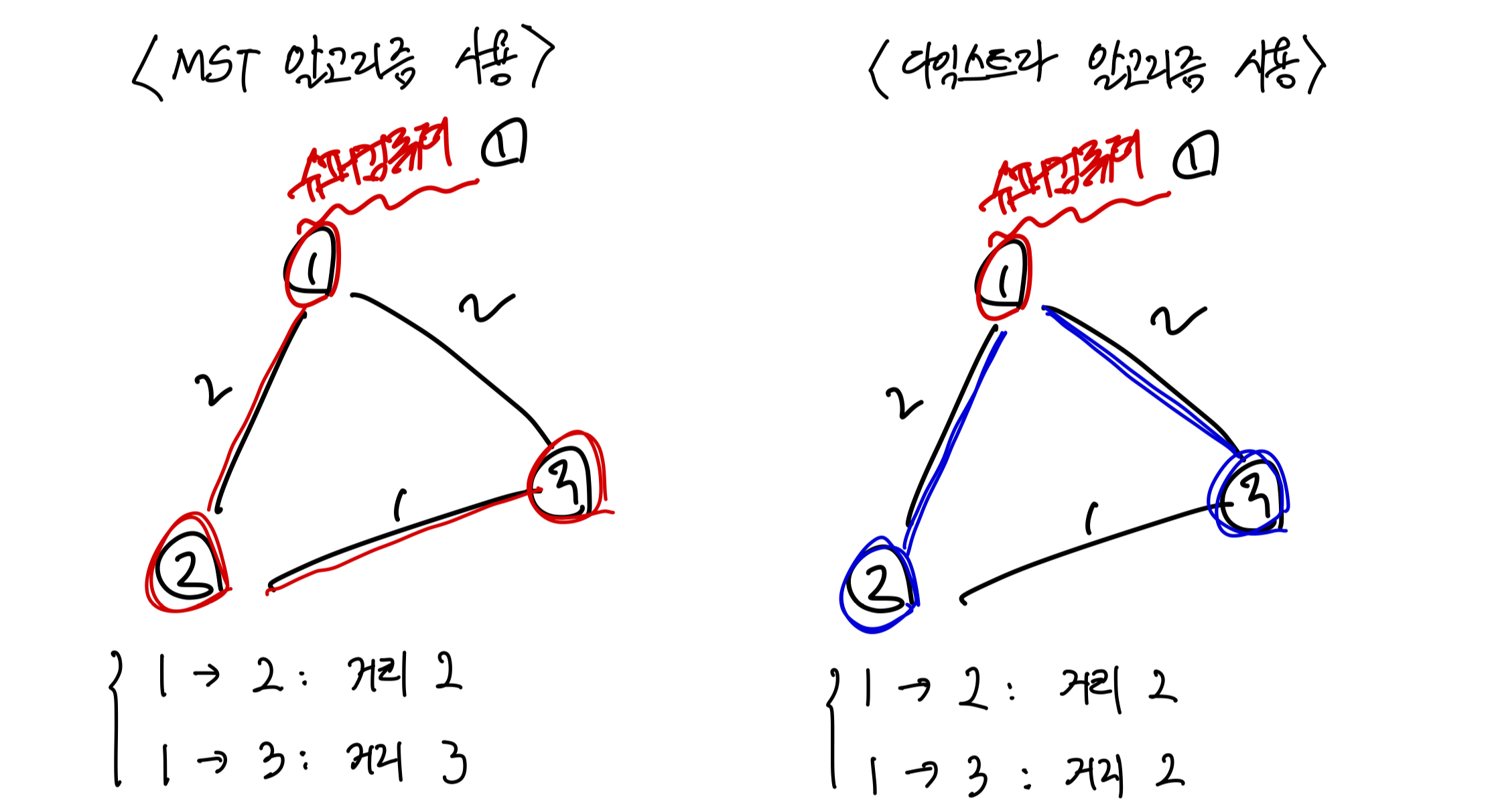
위 사진을 보면, 두 알고리즘의 차이점을 직감할 수 있을 것이다. 정리하자면 간선의 최소합 과 최단 거리 와는 별개의 영역인 것이다.

사고 과정 (2) ‼️

그래서 나는 가중치가 1이 아닌 그래프에 대한 최단 거리를 구하기 위해서 다익스트라 알고리즘을 사용하기로 마음 먹었다. 마음은 먹었지만, 구현은 또 쉽지 않았다. 골드 3 이상의 다익스트라 관련 문제들을 풀어보니 경로 역추적 과정이 들어간 경우가 빈번했다. 10분 정도 생각한 후, 다음과 같은 과정을 생각해냈다.

1번 정점을 시작으로 다익스트라 알고리즘을 구현한다. (경로 역추적 과정까지 포함)
이후, 1번 노드에서 시작하여 2 ~ n번 노드까지의 경로를 역추적하면서 만나는 간선들을 저장한다.
이때, 간선들을 Set 에 간선 번호를 오름차순으로 정렬하여 튜플로 저장한다.
3-1. (3, 1) 과 (1, 3)은 같은 간선이지만, Set에 걸러지지 않으므로 오름차순으로 정렬하여 저장한다.
모든 과정 이후에 Set에 저장된 원소의 개수와 각 튜플들을 반환한다.

이렇게 코드를 구현하고, 제출한 결과 정답 판정을 받았다!

코드

오답 코드 (Kruskal 풀이)

from sys import stdin

input = stdin.readline


def find(x):
    if uf[x] != x:
        uf[x] = find(uf[x])
    return uf[x]


def union(x, y):
    x_root, y_root = find(x), find(y)
    if x_root == y_root:
        return

    if x_root > y_root:
        x_root, y_root = y_root, x_root

    uf[y_root] = x_root


n, m = map(int, input().split())  # 1 ≤ n ≤ 1_000

edges = []
uf = [i for i in range(n + 1)]
for _ in range(m):
    a, b, c = map(int, input().split())
    edges.append((c, a, b))

# 통신 시간 순서대로 오름차순 정렬
edges.sort()

cnt = 0
mst = []
total = 0
for cost, a, b in edges:
    if find(a) != find(b):
        union(a, b)
        total += cost
        cnt += 1
        mst.append((a, b))

print(cnt)
for a, b in mst:
    print(f"{a} {b}")

정답 코드 (Dijkstra 풀이)

from sys import stdin
from heapq import heappush, heappop

input = stdin.readline


def save_trace(path):
    global ans

    for e in range(2, n + 1):
        trace = []
        curr = e
        while curr != -1:
            trace.append(curr)
            curr = path[curr]

        for i in range(len(trace) - 1, 0, -1):
            lst = sorted([trace[i], trace[i - 1]])
            ans.add(tuple(lst))


def dijkstra(s):
    INF = int(1e9)
    dist = [INF for _ in range(n + 1)]
    path = [-1 for _ in range(n + 1)]

    dist[s] = 0
    pq = [(0, s)]
    while pq:
        min_dist, cur_v = heappop(pq)

        if min_dist != dist[cur_v]:
            continue

        for nxt_v, nxt_dist in vertex[cur_v]:
            new_dist = min_dist + nxt_dist
            if new_dist < dist[nxt_v]:
                dist[nxt_v] = new_dist
                path[nxt_v] = cur_v
                heappush(pq, (new_dist, nxt_v))

    save_trace(path)


n, m = map(int, input().split())  # 1 ≤ n ≤ 1_000
vertex = [[] for _ in range(n + 1)]
for _ in range(m):
    a, b, c = map(int, input().split())
    vertex[a].append((b, c))
    vertex[b].append((a, c))

ans = set()
dijkstra(1)
print(len(ans))
for a, b in list(ans):
    print(f"{a} {b}")