[백준 1644] 소수의 연속합 (Python)

김용범·2024년 12월 11일

문제 💁🏻‍♂️

해결 과정

이 문제를 해결하기 위해서 좀 긴 시간을 고민했다. 우선, 1 <= N <= 4_000_000 인 범위에서 소수만을 구하는 것은 에라토스테네스의 체 알고리즘을 통해 빠르게 구할 수 있다. 그러면 연속된 소수들의 합으로 나타낼 수 있는 경우의 수는 어떻게 구할 것인가... O(N^2)으로는 절대 해결이 안될 것이다.

사고 과정 (1) ❗️

처음에는 투 포인터 기법을 활용해서 문제를 접근했다. left, right 변수를 두어 양쪽 변수들을 조절하면서 경우의 수를 구하려고 했다.

left = 0, right = N 으로 둔다.
0번째 소수부터 쭉 더해가면서 N보다 커지기 직전까지 구한다.
같다면 -> 경우의 수를 카운트해준다. / 더 커졌다면 -> 해당 위치로 right 값을 갱신한다.
left 값을 오른쪽으로 한 칸 움직이면서 1번부터 다시 반복한다.

이렇게 풀이해보려고 했으나, 구현하는 부분에서 큰 어려움을 느꼈다.

사고 과정 (2) ‼️

그래서 나는 연속된 이라는 단어에 집중했다. 연속된 소수합이라는 것을 곱씹어보니 떠오르는 단어가 하나 있었다. 그것은 바로 구간합 이었다. 우선, 구간합을 다 구하기에는 4_000_000까지의 소수가 283,146 개가 있으므로 시간 복잡도가 너무 높고, 계산량이 너무 많으므로 시간초과가 날 것이다. 그래서 생각한 것은 다음과 같다.

어차피 연속합을 구하는 것이기 때문에, 첫번째 소수인 2부터 계속 더해가다보면 얼마 안 있어 4_000_000보다 커질 것이다. 즉, 시간 복잡도가 절대 283,146개의 소수를 전부 확인하지 않을 것이므로 충분할 것이다.
2부터 계속 더해가면서 각 dp 배열에 해당 연속합으로 나올 수 있는 경우를 1개씩 증가시켜주고, 최종적으로는 그냥 dp[n] 에 저장된 값을 출력하자.

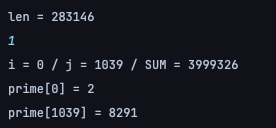
위 사진과 같이 실제로, 최초의 소수인 2부터 계속 소수들만 더해갔을 때, 1040번째 소수인 8291까지의 연속합이 3_999_326이다. 즉, 2중 for 문을 돌려보아도 1000^2 = 10^6 격이다. 연속합의 시작 위치가 높아질수록 인덱스는 더욱 빠르게 증가하기 때문에 시간 복잡도가 더욱 줄어들 것이 확실했다. 이를 토대로 코드를 구현해보니 정답 판정을 받을 수 있었다!

코드

정답 코드

from sys import stdin
from math import isqrt

input = stdin.readline

LEN = 4_000_000
# 에라토스테네스의 체 구현
sieve = [False, False] + [True] * (LEN - 1)
for i in range(2, isqrt(LEN) + 1):
    if sieve[i]:
        for j in range(i * i, LEN + 1, i):
            sieve[j] = False  # 합성수 제거

primes = [i for i in range(2, LEN + 1) if sieve[i]]
dp = [0 for _ in range(LEN + 1)]
n = int(input().rstrip())

for i in range(len(primes)):
    SUM = 0
    for j in range(len(primes)):
        # 범위를 넘거나, 최댓값을 뛰어넘는다면 break
        if i + j >= len(primes) or SUM + primes[i + j] > LEN:
            break
        SUM += primes[i + j]
        dp[SUM] += 1

print(dp[n])

유형: 에라토스테네스의 체 + DP(구간합 개념)