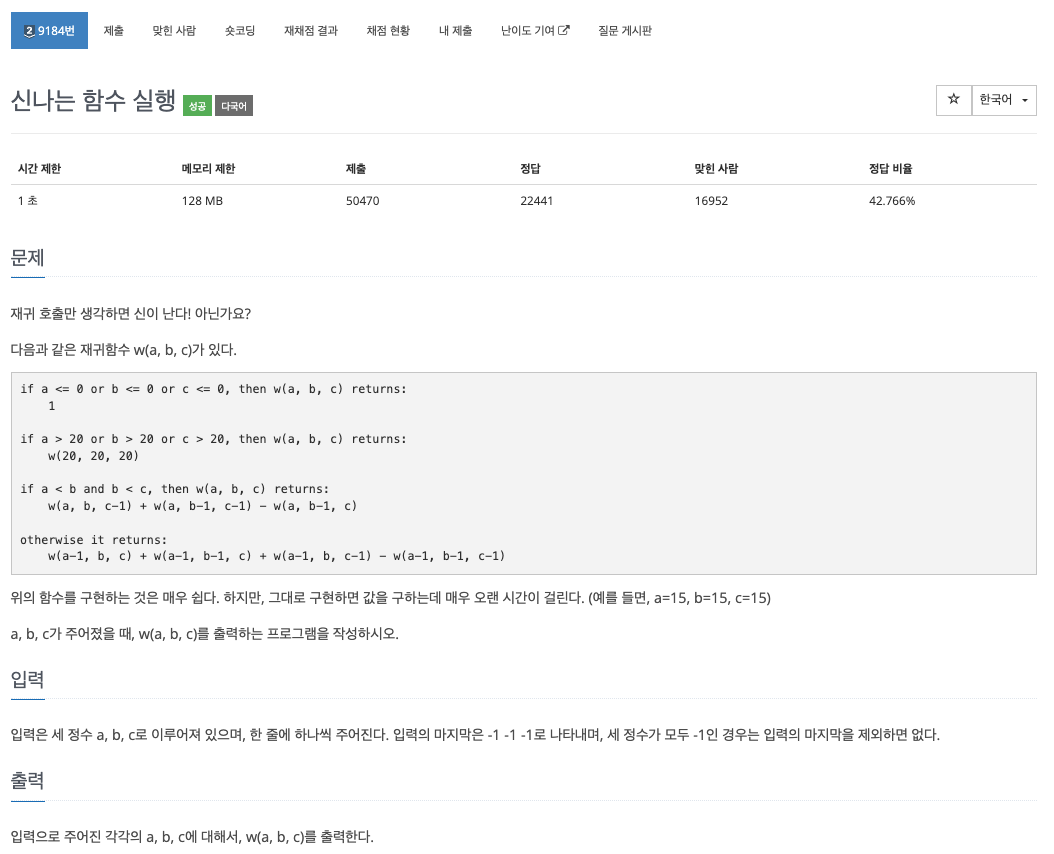
문제 💁🏻♂️
해결 과정
문제를 보자마자 바로 재귀 개념이 들어갈 것임을 알 수 있었다. 재귀의 구조를 파악하기 위해서 w(2, 2, 2)를 직접 종이에 적어봤다. 숫자가 낮음에도 불구하고, 재귀 깊이가 상당히 길어지고, 재귀 횟수가 상당하다는 것을 느낄 수 있었다. 이 느낌은 마치 대표적인 다이나믹 프로그래밍 문제인 피보나치 함수 를 메모이제이션 방법으로 풀이하는 것과 같은 느낌이었다.
사고 과정 (1) ❗️
메모이제이션 방식을 사용하는 것까지 느낌이 왔지만, 문제는 다이나믹 프로그래밍을 어떻게 적용시킬까 였다. 손으로 직접 써내려가는 것은 불가능했고, 머릿속으로 곰곰히 생각해봤지만 딱히 마땅한 풀이 과정이 떠오르지 않았다. 알고리즘 분류를 봐도 역시나 재귀, 다이나믹 프로그래밍 이라는 정보 말고는 얻을 수 있는 게 없었다. 결국 해설이 잘 된 블로그를 하나 찾아서 공부했다.
사고 과정 (2) ‼️
문제에서 주어진 재귀 함수가 있기 때문에 이를 그대로 사용하면서 메모이제이션 기법을 적용하면 됐다. 나는 메모이제이션 개념을 잘 알지 못하고 있었던 것 같다.
메모이 제이션이란, 컴퓨터 프로그램이 동일한 계산을 반복해야할 때,
이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다.
동적 계획법의 핵심이 되는 기술이다.
출처: https://ko.wikipedia.org/wiki/메모이제이션이러한 메모이제이션 개념을 적용해보자. 전략은 다음과 같다.
- 처음 방문하는 곳이면 계산을 통해 얻은 값을 메모리(배열 또는 리스트)에 저장한다.
- 재방문을 할 경우, 해당 값을 다시 계산하는 것이 아니라 저장된 값을 불러온다.
여기서 바로 3중 dp 배열이 도입된다. 사실 1차원, 2차원 dp 배열은 자주 봤어도 3중 dp 배열은 처음 보았다. 그래서 접근을 쉽게 하지 못한 것 같기도 하다. 너무 스스로에 대한 생각을 한계로 두지 말자 문제의 조건 중에서 -50 <= a, b, c <= 50 이라고 주어져서 3중 dp 배열을 각각 50개로 둬야 한다고 생각할 수 있지만, w 함수를 잘 살펴보면 a, b, c 변수 중 하나라도 20이 넘어가면 w(20, 20, 20) 을 호출한다. 즉, 각 3중 dp 각각 최대의 길이를 20으로 설정하면 된다. (실제로는 인덱싱을 편리하게 하기 위해서 21로 설정하자.)

세번째 elif 문을 살펴보면 다음과 같다.
elif dp[a][b][c] != 0:
return dp[a][b][c]이 함수가 메모이제이션의 정수이다. 즉, 이미 계산한 결과가 저장되어있으면(!= 0) 계산을 더 진행하지 않고, dp[a][b][c] 값을 return 하기만 하면 된다. 4번째, 5번째 if ~ else함수 역시 메모이제이션을 활용한 함수이다.
elif a < b < c:
dp[a][b][c] = w( ~~ )
return dp[a][b][c]
else:
dp[a][b][c] = w( ~~ )
return dp[a][b][c]이 함수들은 조건에 맞는 함수식을 수행하되, 그 수행한 결과를 바로 dp[a][b][c] 에 저장하고, 그 값을 바로 return 하면 된다. 이렇게 메모이제이션을 적용하여 코드를 작성해서 제출한 결과는!

정답 판정을 받았다!
코드
정답 코드
from sys import stdin
input = stdin.readline
def w(a, b, c):
if a <= 0 or b <= 0 or c <= 0:
return 1
elif a > 20 or b > 20 or c > 20:
return w(20, 20, 20)
elif dp[a][b][c] != 0:
return dp[a][b][c]
elif a < b < c:
dp[a][b][c] = w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c)
return dp[a][b][c]
else:
dp[a][b][c] = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1)
return dp[a][b][c]
dp = [[[0 for _ in range(21)] for _ in range(21)] for _ in range(21)]
while True:
a, b, c = map(int, input().split())
if a == -1 and b == -1 and c == -1:
break
print(f"w({a}, {b}, {c}) = {w(a, b, c)}")
