[백준 17253] 삼삼한 수 2 (Java)

문제 💁🏻‍♂️

문제 링크 - 백준 17253 삼삼한 수 2

해결 과정

solved.ac 마라톤 문제로 해당 문제를 접했다. 처음 문제를 보면서 느꼈던 점은 입력으로 주어진 최댓값이 너무 크다는 점이었다. 즉, N의 범위가 9,223,372,036,854,775,807보다 작거나 같은 음이 아닌 정수 N 였다. 파이썬이었다면 신경을 안 썼겠지만, Java로 문제를 풀어보는 연습을 해보니까 값의 범위가 굉장히 신경이 쓰였다. Long.MAX_VALUE 를 출력해보니 문제에서 주어진 N으로 가능한 최댓값 숫자가 나온 것을 확인했다. 또한, 3의 몇 제곱까지가 Long.MAX_VALUE 이내로 safe한지 for문을 통해서 확인해본 결과 3^39 까지 가능했다. 즉, 거듭제곱의 인덱스 범위는 0 ~ 39 까지 가능했다. 처음에는 백트래킹으로 문제를 풀이해보려고 했지만, 2^39 라는 경우의 수는 10^9을 아득히 넘어서기 때문에 불가능했다.

사고 과정 ❗️

그럼 이 문제를 어떻게 해결할 수 있을까? dp로 풀이하기에는 메모리 제한에 반드시 걸릴만큼 N의 범위가 넓었고, 그렇다고 그래프로 접근하자니 그것 또한 이상했다. 요즘에 다양한 유형의 문제들을 접하고 나니까 오히려 방법의 수가 많아져서 사고가 복잡해짐을 느꼈다.

20분 동안 고민해보다가 블로그를 참고했는데, 정말 생각지도 못한 해설이 존재했다. 3의 거듭제곱으로만 이루어진 숫자는 결국 주어진 숫자 N을 3진법으로 나타냈을 때, 각각의 진법수가 0 또는 1로 이루어져야 한다는 것이다. 즉, 만약 3진법 i번째 자리가 2라면 2*3^i 이기 때문에 3의 거듭제곱만으로 표현할 수 없다는 논리였다. 예제로 주어진 숫자 2개를 예로 들면 다음과 같다.

예제 1) N = 109 -> 삼삼한 수 O

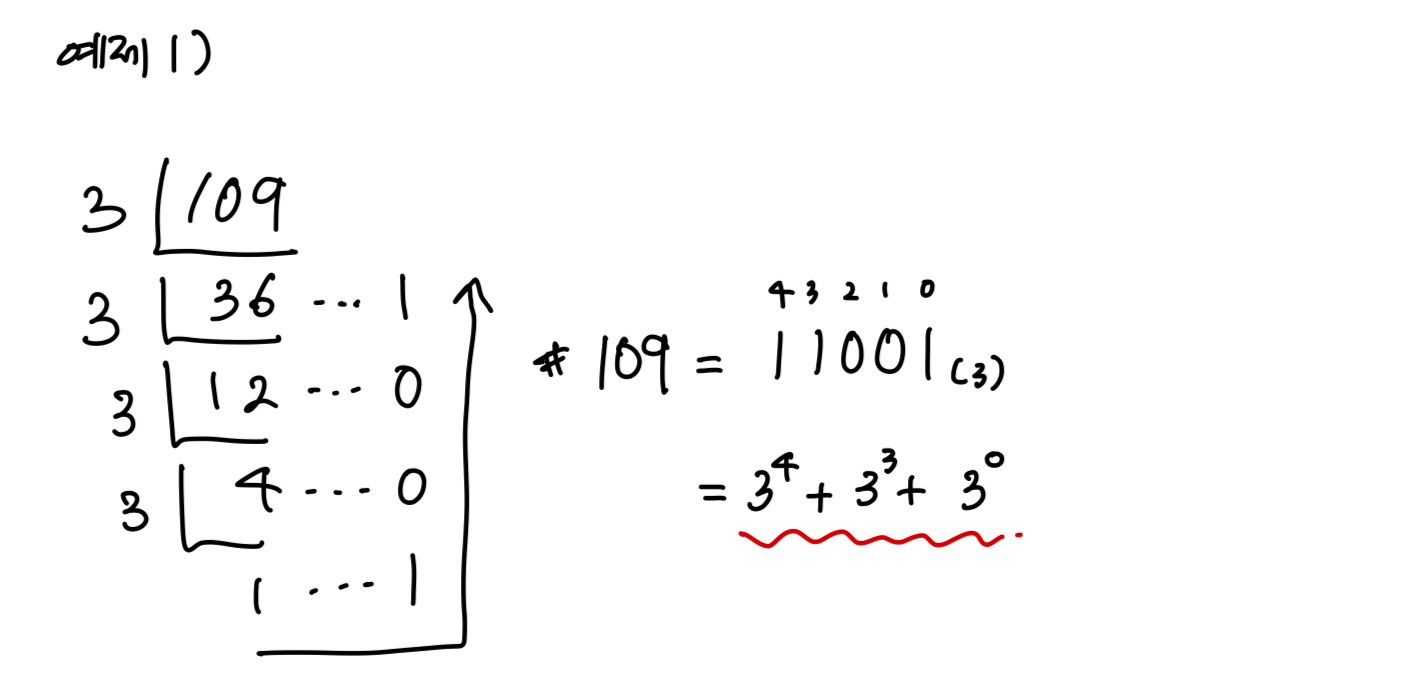
예제 2) N = 298 -> 삼삼한 수 X

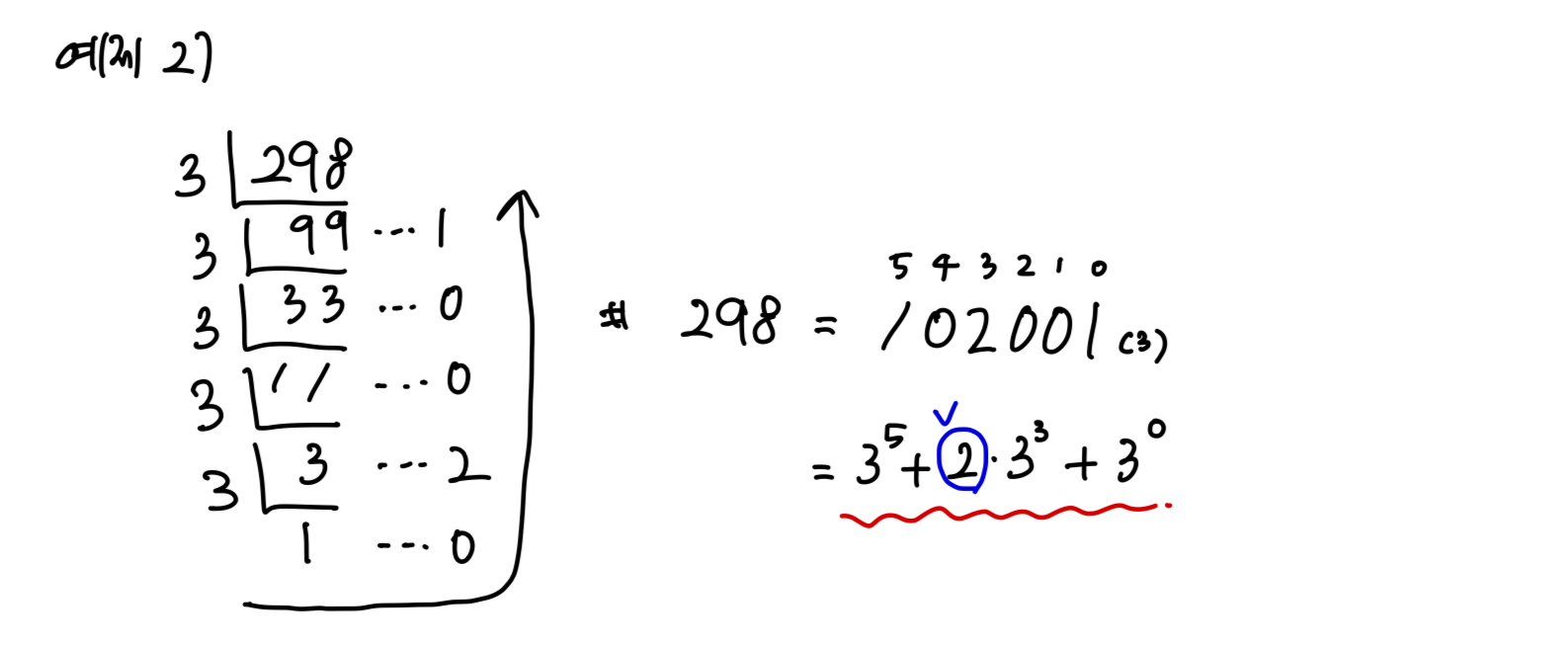
위 로직을 코드로 구현하여 제출해보니 정답 판정을 받았다! 이렇게 비트 단위로 접근하여 해결할 수 있는 풀이도 있다니... 정말 재밌는 것 같다!

코드

정답 코드

import java.util.*;
import java.io.*;

class Main {

    static Scanner sc = new Scanner(System.in);
    static boolean flag = true;
    static long N;

    public static void main(String[] args) {

        N = sc.nextLong();

        if (N == 0)
            flag = false;

        while (N > 0) {

            if (N % 3 == 2) {
                flag = false;
                break;
            }

            N /= 3;
        }

        System.out.println(flag ? "YES" : "NO");

    }
}

Reference

• https://2jinishappy.tistory.com/25