[백준 1937] 욕심쟁이 판다 (Python)

김용범·2024년 12월 20일

백준 코딩테스트

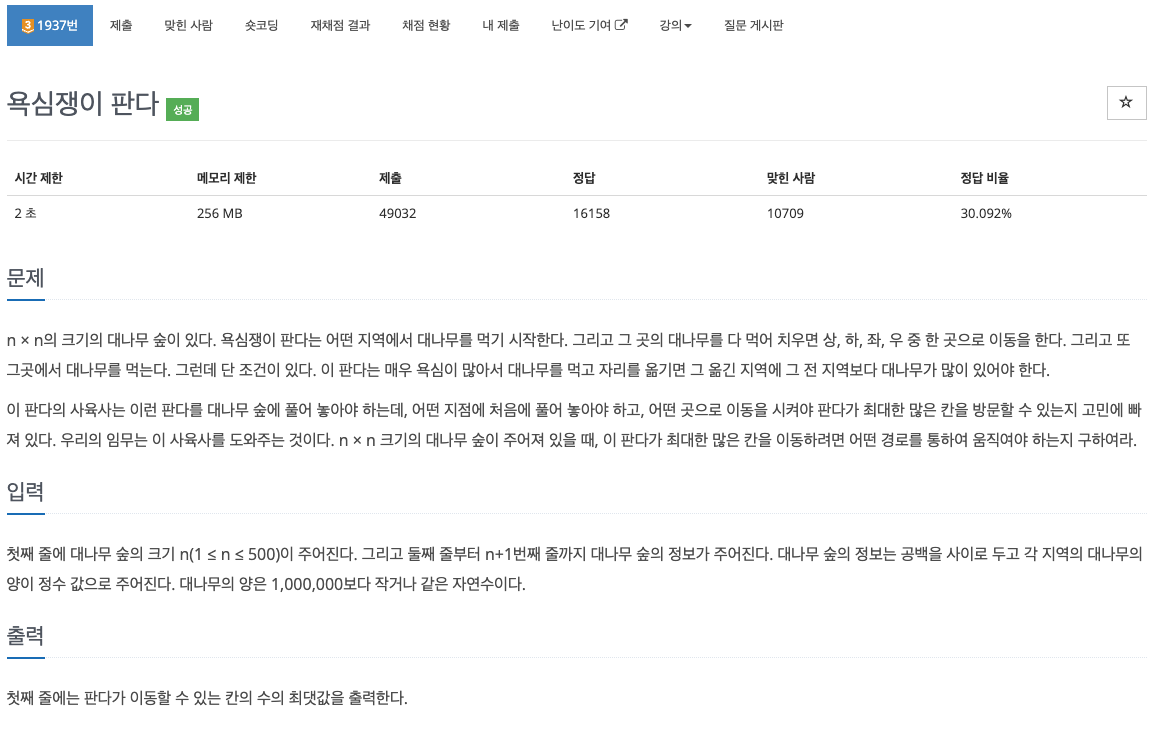
문제 💁🏻‍♂️

문제 링크 - 백준 1937 욕심쟁이 판다

해결 과정

이 문제를 읽고 나서 바로 그래프 문제라는 것을 깨달았다. 판단 근거는 다음과 같다.

상, 하, 좌, 우 이동해야한다.
옮긴 지역에 그 전 지역보다 대나무가 많이 있어야 한다는 조건 즉, 현재 노드와 다음 노드를 비교해야한다.
주어진 조건으로 최대한 많은 칸을 움직여야한다.

사고 과정 (1) ❗️

그래프 문제라는 것을 깨달았고, 한 노드에서 시작하여 갈 수 있는 최대한 많은 칸을 가야하기 때문에 DFS 탐색 자료구조를 사용하기로 결심했다. DFS를 사용한 로직은 다음과 같다.

최댓값을 전역으로 선언한다.
모든 노드를 방문하며 DFS 탐색을 실행한다. 방향성이 정해져있기 때문에 방문 여부는 따로 체크하지 않는다.
범위를 넘지않고, 현재 노드보다 다음 노드가 더 큰 경우에만 이동하도록 하고, 계속해서 전역으로 선언한 최댓값을 갱신해준다.
모든 탐색을 끝난 후, 최댓값을 출력한다.

이러한 로직으로 제출한 결과, 시간초과 & 메모리 초과 판정을 받았다. 처음에는 이해가 가지 않았다. 완전 탐색을 하긴 했지만, n의 범위가 1 ≤ n ≤ 500 이었고, 경로에 대한 시간 복잡도는 대략 500 x 500 = 250,000 정도이다. 방향성이 큰 값을 향해서만 가도록 정해져있기 때문에 각 노드마다 4방향 탐색을 하더라도 충분할 것이라고 생각했는데, 내가 판단을 잘못했다.

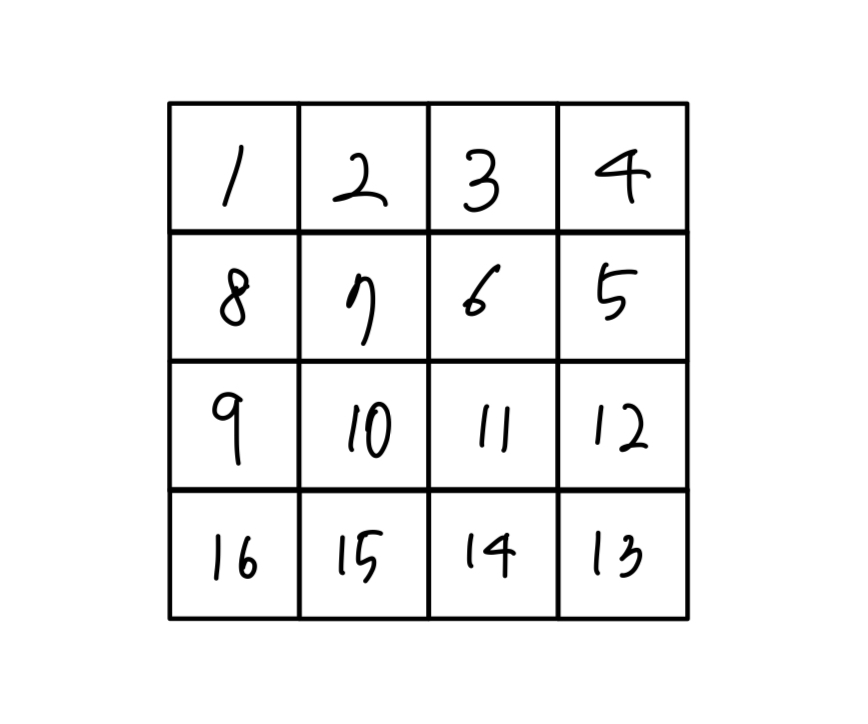
위 그림에서 각 숫자들이 노드 번호라고 할 때, 1번 노드만 생각하자. 상, 하, 좌, 우 범위를 넘지않고, 큰 값만을 찾아가기 위해서 정말 여러 방향으로 움직이며 16을 향해 갈 것이다. 탐색을 끝내고, 2번 노드로 움직여서 다시 DFS 탐색을 하려고 한다면, 1번 노드에서 시작했던 것과 거의 비슷하게 움직일 것이다. 이 MAP이 500 x 500 이라고 생각한다면 정말 많은 탐색을 할 것으로 예상된다.

위 그림 예시를 처음 작성한 코드로 실행하고, 함수 내 동작 횟수를 다음과 같은 코드로 카운팅 해봤다.

def dfs(cur_y, cur_x, cnt):
    global MAX, total_move

    total_move += 1 # 동작 횟수 증가 
    MAX = max(MAX, cnt)
    for dy, dx in zip(dys, dxs):
        nxt_y, nxt_x = cur_y + dy, cur_x + dx
        if 0 <= nxt_y < n and 0 <= nxt_x < n and MAP[cur_y][cur_x] < MAP[nxt_y][nxt_x]:
            dfs(nxt_y, nxt_x, cnt + 1)

그 결과 총 546번 의 탐색을 실행한 것을 확인할 수 있었다. 죽, 4 x 4 = 16 이 아니라 4 x 4 MAP임에도 불구하고 500번이 넘는 탐색을 한 것이다. 500 x 500 MAP 에서 시간초과가 나는 현상은 지극히 당연한 결과였다.

사고 과정 (2) ‼️

시간초과가 났던 원인은 방문 처리를 하지 않았기 때문이다. 즉, 선언했던 dp 2중 리스트를 전혀 사용하고 있지 않아서 생긴 문제였다. 다이나믹 프로그래밍 기법을 같이 적용하려고 하니, 감이 아예 잡히지 않아 이를 잘 풀이한 블로그를 찾아서 공부했다. 메모이제이션을 활용하여 DFS 탐색을 하면서도 현재 위치에서 최대로 뻗어나갈 수 있는 최대 노드 개수를 지속적으로 갱신해보자. 그러면 방문했던 곳을 재방문 시 해당 노드에 저장된 값을 통해 더 이상의 탐색을 하지 않아도 되므로 시간 절약을 할 수 있다.

전역으로 최댓값을 1로 초기화한다.
모든 노드를 탐색하지만, dp값이 -1(초기값)인 경우에만 DFS 탐색을 한다.
cnt 값을 1로 설정하고, dfs를 돌때마다 다음 노드의 dp값을 return 받으면서 cnt값에 더해주도록 한다. 만약 다음 노드를 어디선가 방문하여 -1값이 아니라면, 해당 노드에 저장된 값을 바로 return 받는다.
재귀를 거듭하면서 저장된 dp값을 계속 return 받으면서 최초의 시작 노드에는 가장 큰 값이 저장되게 된다. 재귀 과정에서 전역으로 선언한 최댓값을 계속 갱신해준다.
최댓값을 갱신한다.

DFS 탐색은 아무래도 재귀 자료구조이기 때문에 추론하기가 좀 힘든 것 같다. 따라서 정확한 동작 방식을 이해하는 것이 중요하다. 또한, DFS 탐색과 DP 알고리즘이 결합된 문제들이 기업 코테에서도 종종 등장하기 때문에 이와 같은 유형의 문제를 충분히 풀어보는 것도 중요한 것 같다.

DP 알고리즘을 적용하니, 정답 판정을 받았다!

코드

오답 코드 (시간 초과 & 메모리 초과)

from sys import stdin, setrecursionlimit

setrecursionlimit(25 * (10 ** 4))
input = stdin.readline


def dfs(cur_y, cur_x, cnt):
    global MAX

    MAX = max(MAX, cnt)
    for dy, dx in zip(dys, dxs):
        nxt_y, nxt_x = cur_y + dy, cur_x + dx
        if 0 <= nxt_y < n and 0 <= nxt_x < n and MAP[cur_y][cur_x] < MAP[nxt_y][nxt_x]:
            dfs(nxt_y, nxt_x, cnt + 1)


n = int(input().rstrip())

MAP = [list(map(int, input().split())) for _ in range(n)]

MAX = 0
dys, dxs = [-1, 1, 0, 0], [0, 0, -1, 1]
for i in range(n):
    for j in range(n):
        dp = [[-1 for _ in range(n)] for _ in range(n)]
        dfs(i, j, 1)

print(MAX)

정답 코드

from sys import stdin, setrecursionlimit

setrecursionlimit(10 ** 8)
input = stdin.readline


def dfs(cur_y, cur_x):
    global MAX

    if dp[cur_y][cur_x] != -1:
        return dp[cur_y][cur_x]

    dp[cur_y][cur_x] = 1  # 기본 방문 체크
    for dy, dx in zip(dys, dxs):
        nxt_y, nxt_x = cur_y + dy, cur_x + dx
        # 범위를 넘지 않고, 현재 위치의 대나무보다 다음 위치의 대나무가 더 많다면 -> 탐색
        if 0 <= nxt_y < n and 0 <= nxt_x < n and MAP[cur_y][cur_x] < MAP[nxt_y][nxt_x]:
            cnt = 1
            cnt += dfs(nxt_y, nxt_x)
            dp[cur_y][cur_x] = max(dp[cur_y][cur_x], cnt)
            MAX = max(MAX, dp[i][j])

    return dp[cur_y][cur_x]


n = int(input().rstrip())
MAP = [list(map(int, input().split())) for _ in range(n)]
dp = [[-1 for _ in range(n)] for _ in range(n)]

MAX = 1
dys, dxs = [-1, 1, 0, 0], [0, 0, -1, 1]
for i in range(n):
    for j in range(n):
        if dp[i][j] == -1:
            dfs(i, j)

print(MAX)