[백준 11779] 최소비용 구하기 2 (Python)

김용범·2024년 12월 24일

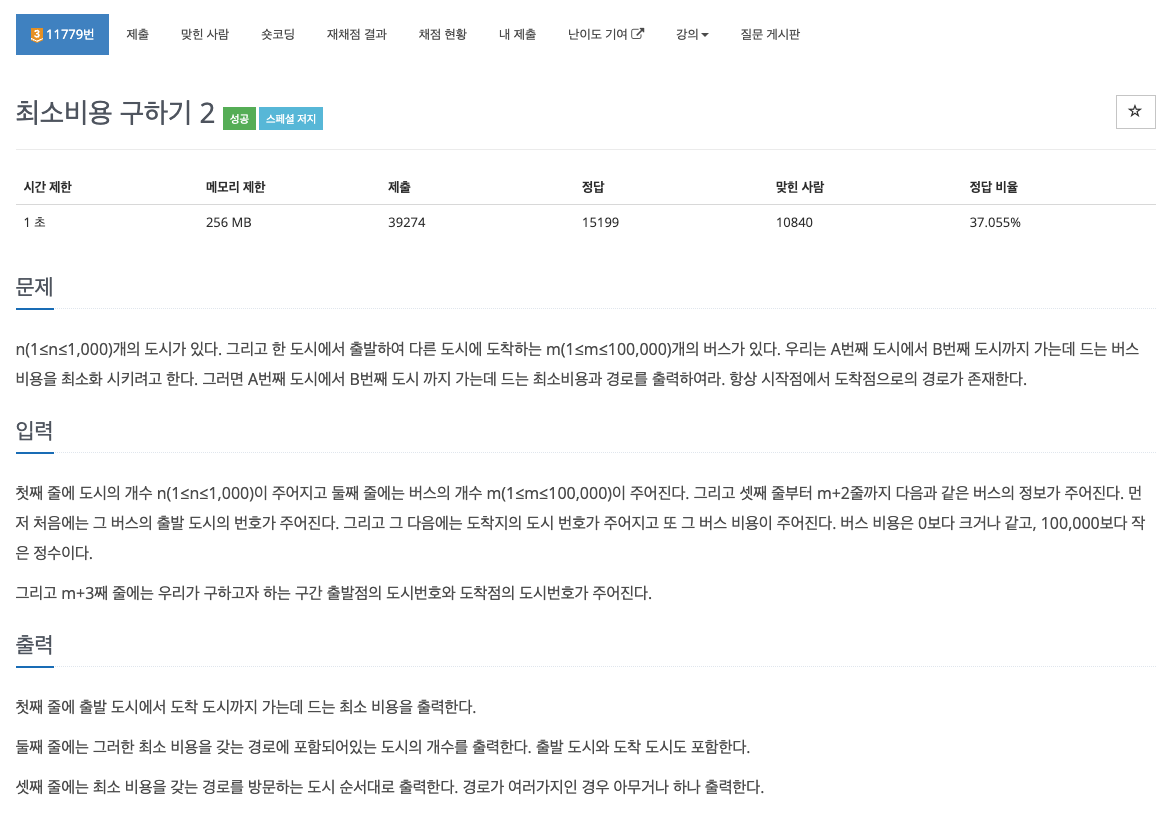
문제 💁🏻‍♂️

해결 과정

이 문제는 전형적인 다익스트라 알고리즘 문제에서 더 나아가 최단 경로를 추적하는 문제이다.

사고 과정 ❗️

우선, 기본 다익스트라 핵심 알고리즘 코드는 다음과 같다.

from heapq import heappush, heappop 

def dijkstra(s, e):
    INF = float('inf')
    dist = [INF for _ in range(n + 1)]

    dist[s] = 0
    pq = [(0, s)]
    while pq:

        min_dist, cur_v = heappop(pq)
        if min_dist != dist[cur_v]:
            continue

        if cur_v == e:
            break

        for nxt_v, nxt_dist in vertex[cur_v]:
            new_dist = min_dist + nxt_dist
            if new_dist < dist[nxt_v]:
                dist[nxt_v] = new_dist
                heappush(pq, (new_dist, nxt_v))

    return dist[e]

이 코드에서 경로를 추적하기 위한 알고리즘을 추가해주면 된다. 여러 블로그들의 도움을 받아 흐름을 이해할 수 있었다. 그 흐름은 다음과 같다.

경로를 추적할 수 있는 path 리스트를 하나 만든다.
최단 거리를 갱신할 때마다 다음 노드 인덱스에 현재 노드 인덱스를 저장 한다.
목적지 노드의 인덱스부터 시작하여 저장된 이전 노드들을 거슬러 올라가면서 경로를 역추적한다.
역추적했기 때문에, 결과로 나온 경로의 순서를 뒤집는다.
4-1. 역추적을 편리하게 하기 위해서 deque의 appendleft를 사용해도 좋을 것 같다.

이런 과정을 거쳐 최단 거리로 움직인 경로를 찾아낼 수 있다.(단, 노드의 저장 순서에 따라 여러가지 경로가 나올 수 있다.)


def get_trace(path, e):
	trace = []  # 경로 저장 리스트 
    curr = e 
    while curr != -1:
    	trace.append(curr) 
        curr = path[curr]  # 경로 역추적 
    
    return trace[::-1]  # 역순 반환 

def dijkstra(s, e):

	path = [-1 for _ in range(n + 1)]  # 경로 저장 리스트 
    
    while pq:
    
    ...
    
    	for nxt_v, nxt_dist in vertex[cur_v]:
        	new_dist = min_dist + nxt_dist
            # 최단 거리를 갱신하는 경우 
            if new_dist < dist[nxt_v]:
            	path[nxt_v] = cur_v  # 다음 노드의 현재 노드를 저장 
    ...
    
    return dist[e], get_trace(path, e)  # 목적지까지 최단 거리와 경로 반환

기존 다익스트라 알고리즘에서 추가된 부분만을 강조하여 작성해보았다. 비록 코드 몇 줄만을 추가했지만, 이걸 생각해내는 게 쉽지 않았다. 이 방법이 응용되어 쓰일 수 있으므로 다음 노드에 현재 노드를 저장하면서 경로를 역추적하는 방법을 기억해두자.

이렇게 공부를 한 다음에 코드를 제출했는데 틀렸다. 왜인지 디버깅하면서 이유를 찾아보니 문제에서 요구하는 조건은 단방향 조건이었다. 그러나, 나는 양방향으로 v1, v2 노드에 서로의 노드를 같이 저장하여 정답을 잘못 출력한 것이었다. 이 조건을 맞추고 다시 제출하니 정답 판정을 받았다!

코드

오답 코드 (오답 요인: 양방향)

from sys import stdin
from heapq import heappush, heappop

input = stdin.readline


def get_trace(path, e):
    trace = []
    curr = e
    while curr != -1:
        trace.append(curr)
        curr = path[curr]

    return trace[::-1]


def dijkstra(s, e):
    INF = float('inf')
    dist = [INF for _ in range(n + 1)]
    path = [-1 for _ in range(n + 1)]

    dist[s] = 0
    pq = [(0, s)]
    while pq:

        min_dist, cur_v = heappop(pq)
        if min_dist != dist[cur_v]:
            continue

        if cur_v == e:
            break

        for nxt_v, nxt_dist in vertex[cur_v]:
            new_dist = min_dist + nxt_dist
            if new_dist < dist[nxt_v]:
                path[nxt_v] = cur_v
                dist[nxt_v] = new_dist
                heappush(pq, (new_dist, nxt_v))

    trace = get_trace(path, e)
    return dist[e], trace


n = int(input().rstrip())
m = int(input().rstrip())

vertex = [[] for _ in range(n + 1)]
for _ in range(m):
    v1, v2, t = map(int, input().split())  # v1 <-> v2: 양방향 t
    vertex[v1].append((v2, t))
    vertex[v2].append((v1, t))

s, e = map(int, input().split())
dist, trace = dijkstra(s, e)

# 정답 출력
print(dist)
print(len(trace))
print(*trace)

정답 코드 (수정 내용: 단방향)

from sys import stdin
from heapq import heappush, heappop

input = stdin.readline


def get_trace(path, e):
    trace = []
    curr = e
    while curr != -1:
        trace.append(curr)
        curr = path[curr]

    return trace[::-1]


def dijkstra(s, e):
    INF = float('inf')
    dist = [INF for _ in range(n + 1)]
    path = [-1 for _ in range(n + 1)]

    dist[s] = 0
    pq = [(0, s)]
    while pq:

        min_dist, cur_v = heappop(pq)
        if min_dist != dist[cur_v]:
            continue

        if cur_v == e:
            break

        for nxt_v, nxt_dist in vertex[cur_v]:
            new_dist = min_dist + nxt_dist
            if new_dist < dist[nxt_v]:
                path[nxt_v] = cur_v
                dist[nxt_v] = new_dist
                heappush(pq, (new_dist, nxt_v))

    trace = get_trace(path, e)
    return dist[e], trace


# 입력 부분
n = int(input().rstrip())
m = int(input().rstrip())

# 풀이 부분
vertex = [[] for _ in range(n + 1)]
for _ in range(m):
    v1, v2, t = map(int, input().split())  # v1 <-> v2: 양방향 t
    vertex[v1].append((v2, t))

s, e = map(int, input().split())
dist, trace = dijkstra(s, e)

# 정답 출력
print(dist)
print(len(trace))
print(*trace)