그리디 (Greedy Algorithm) 공부 및 연습문제 풀이(JAVA) - (백준 11047, 1931, 2217, 1026)

이요환·2022년 9월 21일

처음

이번에는 그리디 알고리즘을 공부했다. 그리디 알고리즘의 정의는, 지금 당장 최적인 답을 근시안적으로 택하는 알고리즘이라고 한다. 역시나 정의만 봐서는 감이 잘 오지 않는다. 바로 문제를 풀어 보면서 감을 잡아봤다.

중간

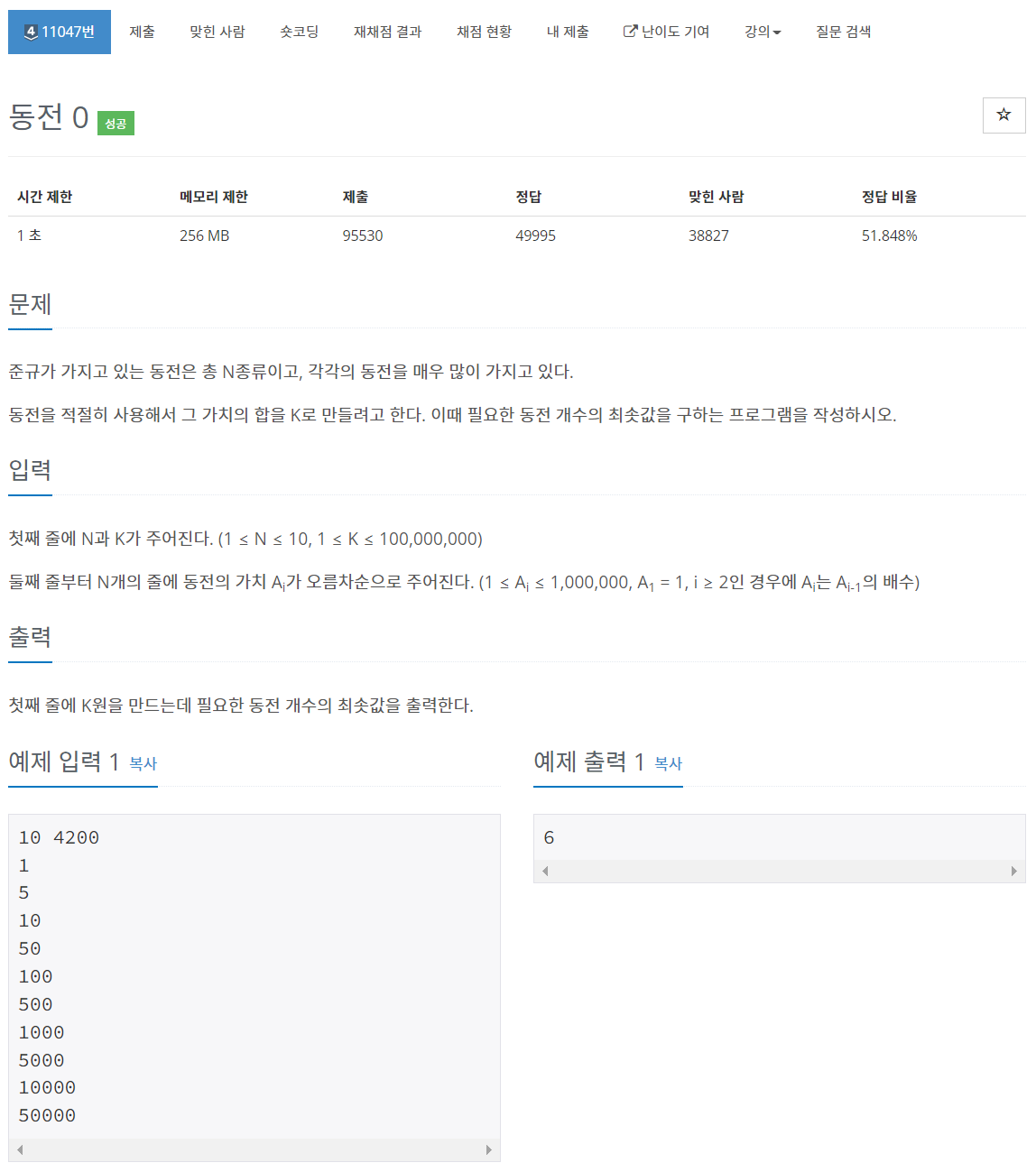DP에서 봤던 문제와 유사해보인다. 차이는 두 가지 인데, 첫번째는 k가 최대 1억이라는 점이고, 두번째는 A가 오름차순으로, 이전 A의 배수로 주어진다는 것이다. 첫번째 조건 때문에 DP로 검사하는 방식은 불가능하다.

두번째 조건을 보자마자 매우 쉬운 풀이를 생각해냈다. 그리디 알고리즘이 뭔지도 모르는 다른 많은 사람들도 그랬을 것 같다. 어떤 동전이 있을 때, 이것이 그 이전 동전들의 배수라는 것은 Aj로 계산할 수 있는 돈은 Aj-1로도 표현할 수 있고, 모든 상황에서 Aj를 사용하는 쪽이 동전이 적다는 것이다. 이렇게 복잡하게 말 안해도 풀이법을 직관적으로 찾아냈을 것이다.

그렇다면 풀이는 가장 큰 동전부터 최대한 많이 써버리는 방식이 된다. 그리고 이것이 바로 그리디 알고리즘이다. -> 현재 상황에서 근시안적으로 최적인 답을 구하는 것!

public class BOJ2217 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(br.readLine());
        }

        Arrays.sort(arr);

        long tmpMax = 0;

        for (int i = n-1; i >= 0 ; i--) {
            if (tmpMax > arr[i]*(n-i)) continue;
            tmpMax = arr[i] * (n - i);
        }
        System.out.println(tmpMax);
    }
}

그리디 알고리즘이라는 거창한 이름 없이도 생각해낼 수 있는 풀이였다. 이 부분에서 그리디 알고리즘의 핵심을 알 수 있는데, BFS, 백트래킹, DP 등등 이런저런 알고리즘으로 풀 수 없거나, 시간 초과가 뜰 것 같으면 이런 정형화된 알고리즘이 아닌 뭔가 빠르고 원시적인 풀이가 필요하다는 것이고, 이것이 바로 그리디 라는 것이다. 그냥 내 나름대로 그리디를 써야하는 상황을 생각해봤다.

그리고 또 주의해야할 점은, 그리디로 풀려고 한다면 내가 생각한 그리디 알고리즘에 문제가 없는지 자세하게 살펴야한다. 이 문제 역시도 Aj가 Aj-1의 배수라는 조건이 있기 때문에 가능했던 것이다.

2. 백준 1931 - 회의실 배정

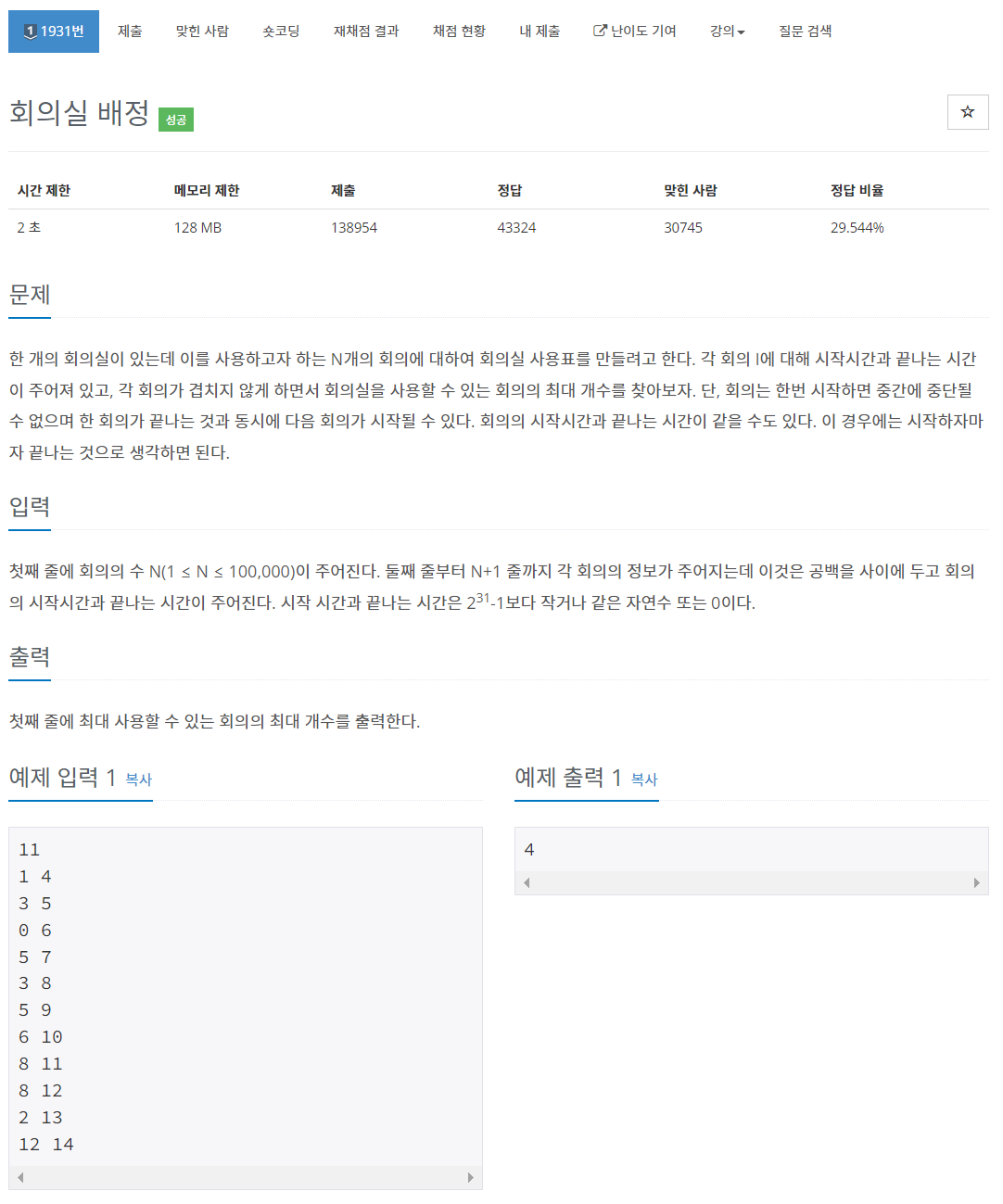DP로 해결한다면, D[i]를 i번째 회의가 끝나는 최소 시간으로 설정해서 O(n^2)의 풀이가 가능 할 것이다. 하지만 회의의 수가 10만이기 때문에 시간 초과가 뜬다.

그리고 이 문제 역시 가만히 들여다보면 뭔가 매우 쉬운 풀이가 있다는 것을 알 수 있다. 그냥 회의를 마치는 시간 순으로 검사를 해가면서, 회의시간이 안겹치면서 가장 빨리 끝나는 회의를 써버리면 되는 것이다.

class Meeting implements Comparable<Meeting> {
    int start;
    int end;

    public Meeting(int start, int time) {
        this.start = start;
        this.end = time;
    }

    @Override
    public int compareTo(Meeting m) {
        if (m.end == this.end) return this.start - m.start;
        return this.end - m.end;
    }

    @Override
    public String toString() {
        return "(" + this.start + ", " + this.end + ")";
    }
}

public class BOJ1931 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        Queue<Meeting> queue = new PriorityQueue<>();

        for (int i = 0; i < n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            queue.offer(new Meeting(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())));
        }
        int answer = 1;
        Meeting prev = queue.poll();
        while (!queue.isEmpty()) {
            Meeting tmp = queue.poll();

            if (prev.end <= tmp.start) {
                answer++;
                prev = tmp;
            }
        }

        System.out.println(answer);
    }
}

정렬은 우선순위 큐에 comparable를 구현한 클래스를 집어넣는 방식으로 했다.

3. 백준 2217 - 로프

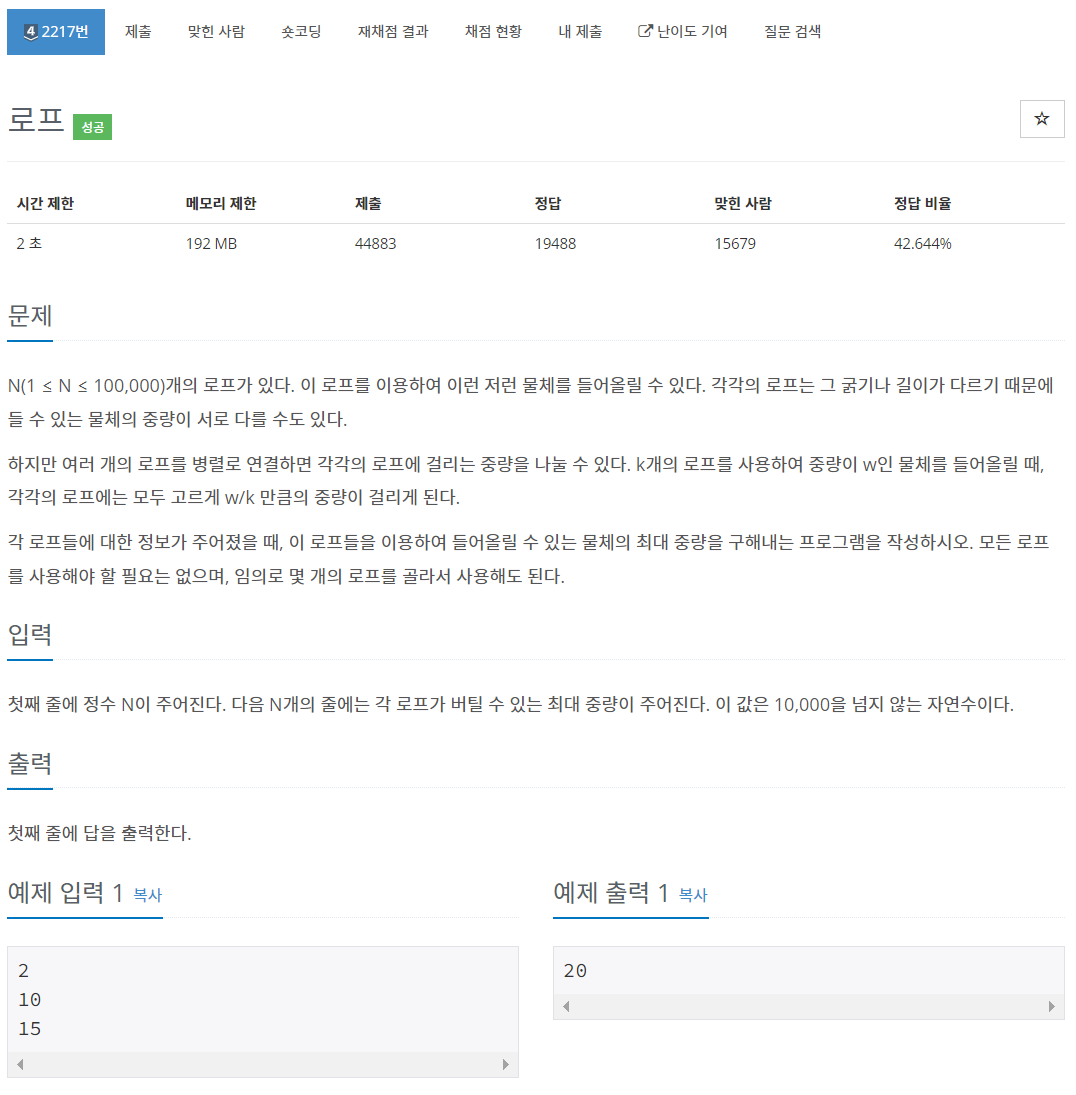우선 너무 당연하게도 가장 중량을 많이 버틸 수 있는 순서대로 로프를 사용해야 할 것이다. 그리고 들 수 있는 무게의 한계는, (현재까지 사용한 로프 중에 가장 약한것*k)가 된다. 로프를 검사해가면서 이 값의 최댓값을 찾으면 된다. 이 때의 시간복잡도는 O(n)이다.

public class BOJ2217 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(br.readLine());
        }

        Arrays.sort(arr);

        long tmpMax = 0;

        for (int i = n-1; i >= 0 ; i--) {
            if (tmpMax > arr[i]*(n-i)) continue;
            tmpMax = arr[i] * (n - i);
        }
        System.out.println(tmpMax);
    }
}

4. 보물 - 백준 1026

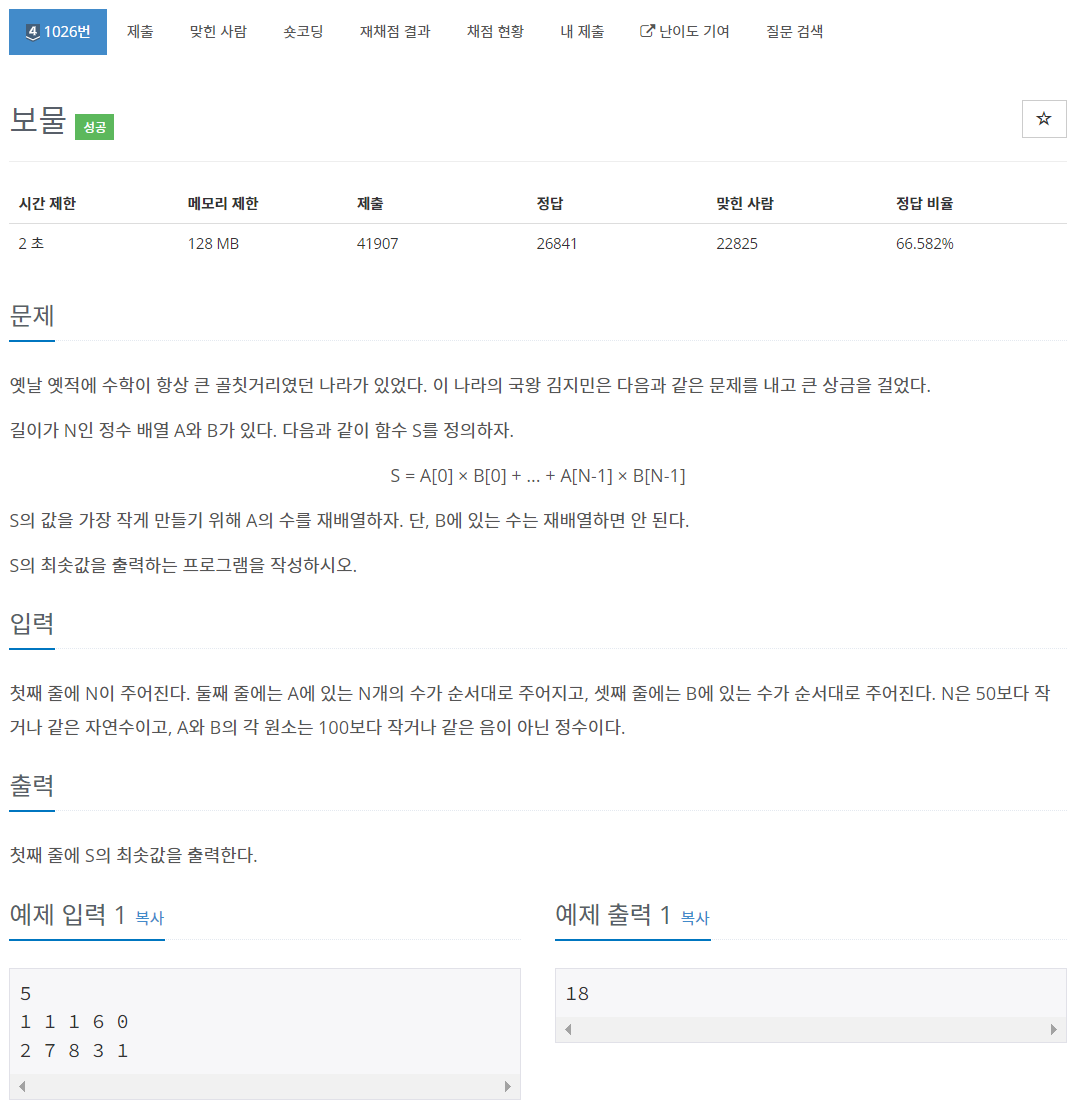두 배열의 원소들 사이의 곱 연산의 값을 최소로 만들기 위해서는 가장 큰 원소에 가장 작은 원소를 곱해야한다.

public class BOJ1026 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        int[] a = new int[n];
        int[] b = new int[n];
        StringTokenizer st = new StringTokenizer(br.readLine());
        for (int i = 0; i < n; i++) {
            a[i] = Integer.parseInt(st.nextToken());
        }
        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < n; i++) {
            b[i] = Integer.parseInt(st.nextToken());
        }

        Arrays.sort(a);
        Arrays.sort(b);

        int answer = 0;

        for (int i = 0; i < n; i++) {
            answer += a[i]*b[n - 1 - i];
        }

        System.out.println(answer);
    }
}