처음
지난 포스팅에 이어 다이나믹 프로그래밍 문제들을 많이 풀었다. 푼 문제가 너무 많은데 비슷한 유형도 많아서, 풀면서 어려움이 있었던, 혼자 해결하지 못했던 문제들만 집중적으로 복습 후 포스팅하려고 한다.
중간
1. 백준 1912 - 연속합
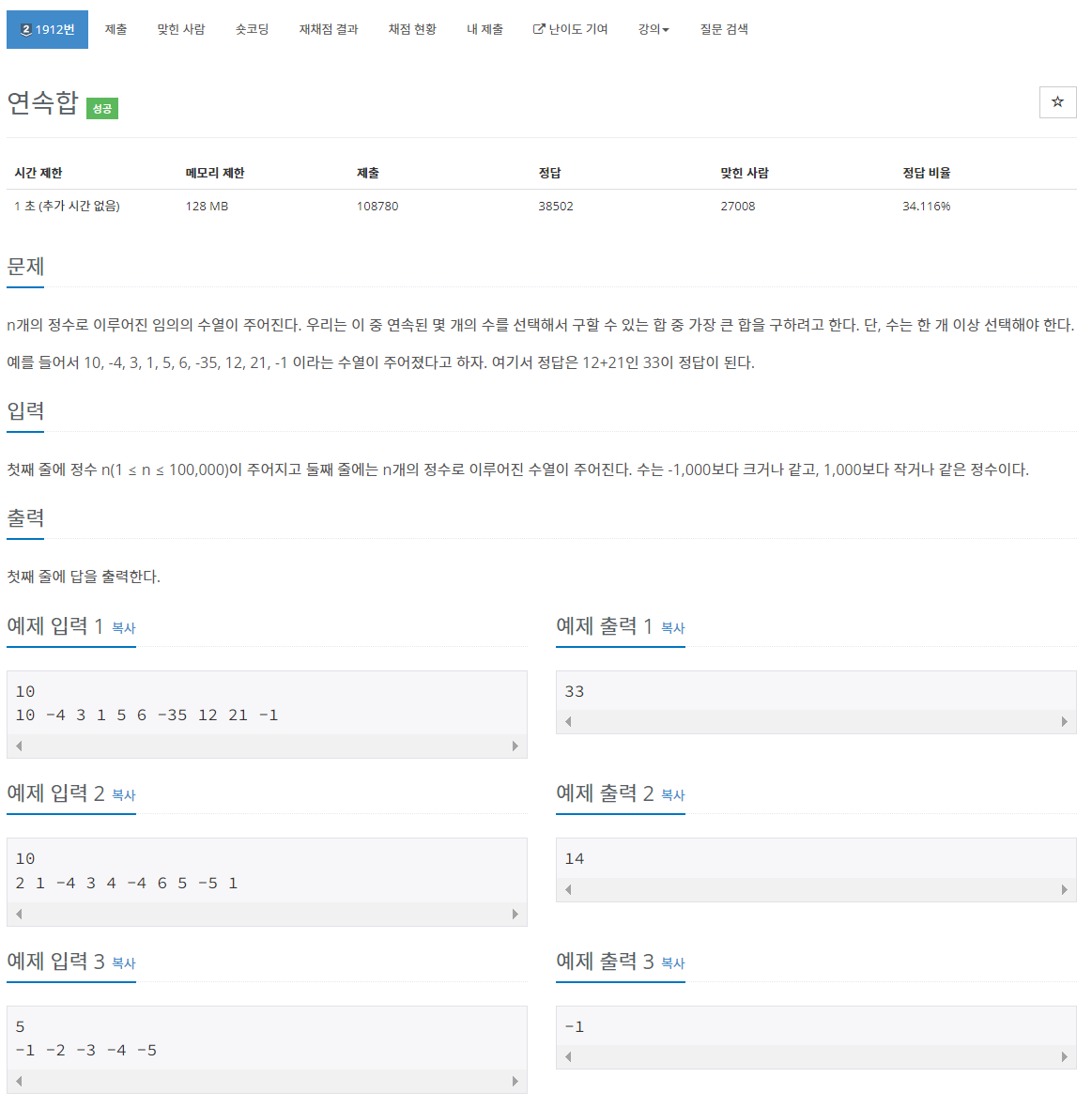점화식 유도가 엄청 쉬운 문제들만 풀다가 처음 접한 조금 까다로운 문제였다. 처음엔 접근 방법을 생각해내지 못했다.
- D[i] = i까지의 배열 중에 arr[i]를 포함하는 최대의 연속합
- D[i] = Math.max(arr[i] + D[i-1], arr[i])
- D[1] = arr[1]
지금까지의 최대합이 자신보다 작으면 이어갈 필요가 없다. 위 과정을 통해 D 배열에는 각 원소(arr[i])가 마지막인 연속합 중의 최댓값이 들어가게 되고, 그 중 최댓값을 찾아 반환하면 된다.
package dynamic.review;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ1912 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n + 1];
int[] d = new int[n + 1];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i < n+1; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
d[1] = arr[1];
long max = arr[1];
for (int i = 2; i < n+1; i++) {
if (d[i-1] + arr[i] > arr[i]) {
d[i] = d[i - 1] + arr[i];
} else d[i] = arr[i];
max = Math.max(d[i], max);
}
System.out.println(max);
}
}
2. 백준 11055 - 가장 큰 증가 부분 수열
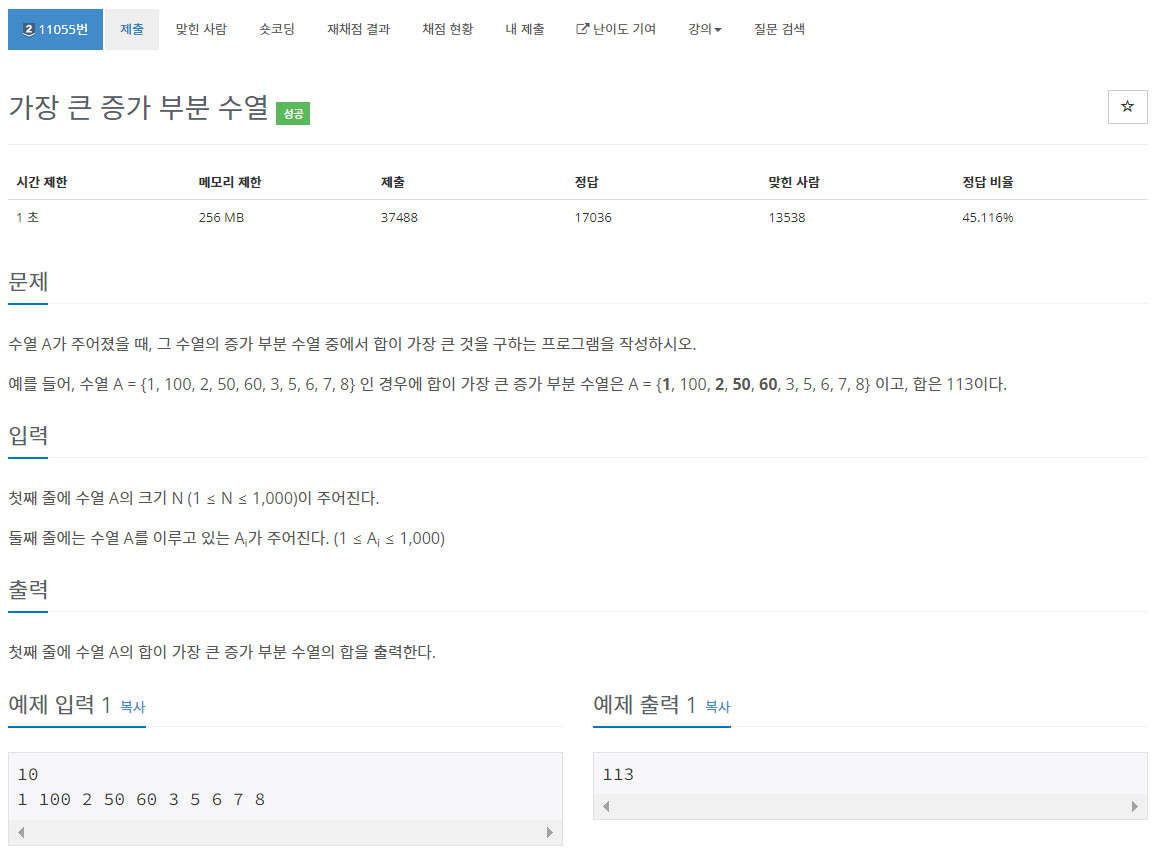이전 문제의 응용된 형태였다. 이전 문제와 달라진 점은 수열이 연속될 필요는 없고, 증가하는 형태여야한다.
- D[i] = i를 마지막 원소로 갖는 증가 부분 수열 중 최대합
- D[i] = arr[i] > arr[j] 를 만족시키는 d[1] ~ D[i-1] 중의 최댓값
N이 최대 1000이기 때문에 가능했다. d[i] 값을 저장할 때, 자신 이전의 최댓값들을 모두 검사하며 이전의 원소보다 증가하는 지 확인한 뒤 최댓값을 갱신해주면 된다.
package dynamic.review;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ11055 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n + 1];
int[] d = new int[n + 1];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i < n + 1; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
d[1] = arr[1];
for (int i = 2; i < n + 1; i++) {
d[i] = arr[i];
for (int j = 1; j < i; j++) {
if (arr[i] > arr[j] && d[i] < d[j] + arr[i]) d[i] = d[j] + arr[i];
}
}
System.out.println(Arrays.toString(d));
}
}
3. 백준 11053 - 가장 긴 증가하는 부분 수열
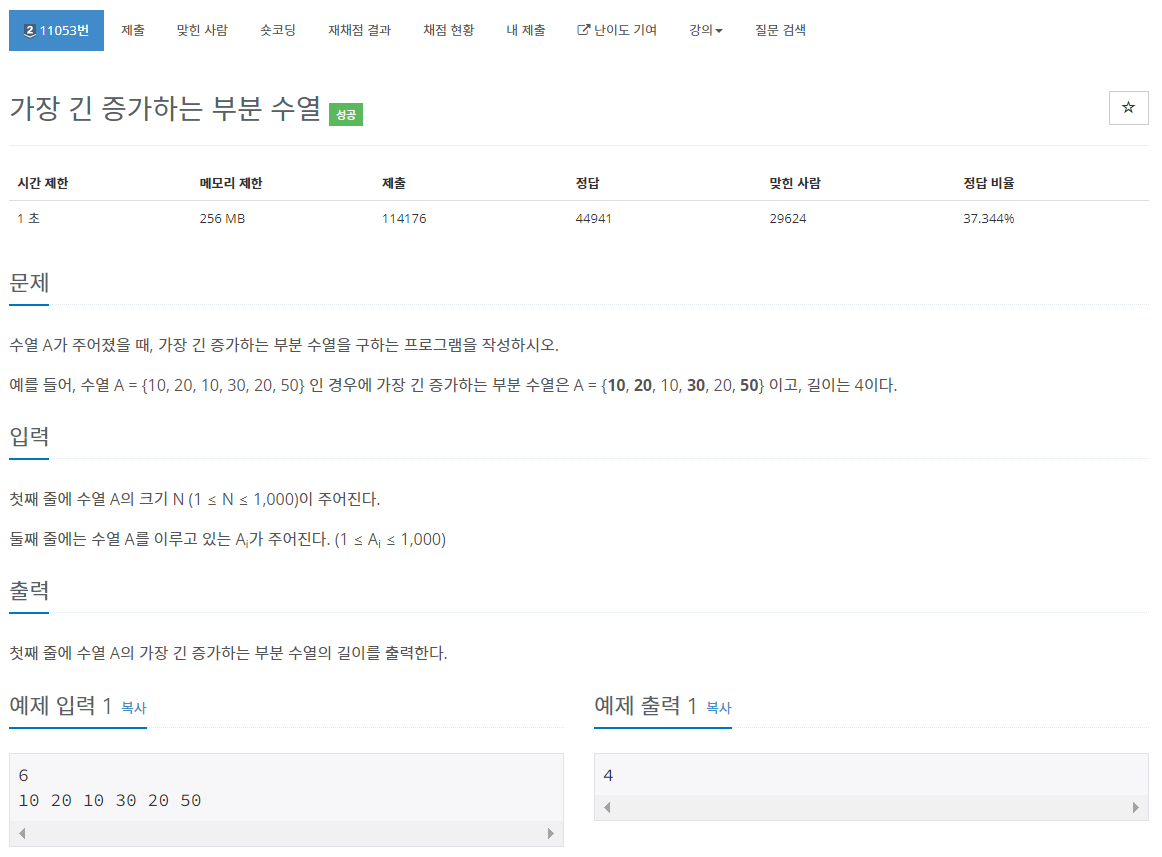이전 문제와 달라진 점은 최대합이 아닌, 최대 원소의 길이를 구해야한다는 것이다. d 배열에 합이 아닌 부분수열의 길이를 저장하면 될 것이다.
- D[i] = i가 마지막 원소인 최대 길이의 증가부분수열의 길이
- 2번 참고
package dynamic.review;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ11053 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
if (n == 1) {
System.out.println(1);
return;
}
int[] arr = new int[n + 1];
int[] d = new int[n + 1];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i < n+1; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
d[1] = 1;
int max = -1;
for (int i = 2; i < n + 1; i++) {
d[i] = 1;
for (int j = 1; j < i; j++) {
//최댓값이 아닌 원소 개수이므로 1을 더해준당.
if (d[j] + 1 > d[i] && arr[j] < arr[i]) d[i] = d[j] + 1;
}
if (d[i] > max) max = d[i];
}
System.out.println(max);
}
}
4. 백준 15486 - 퇴사 2
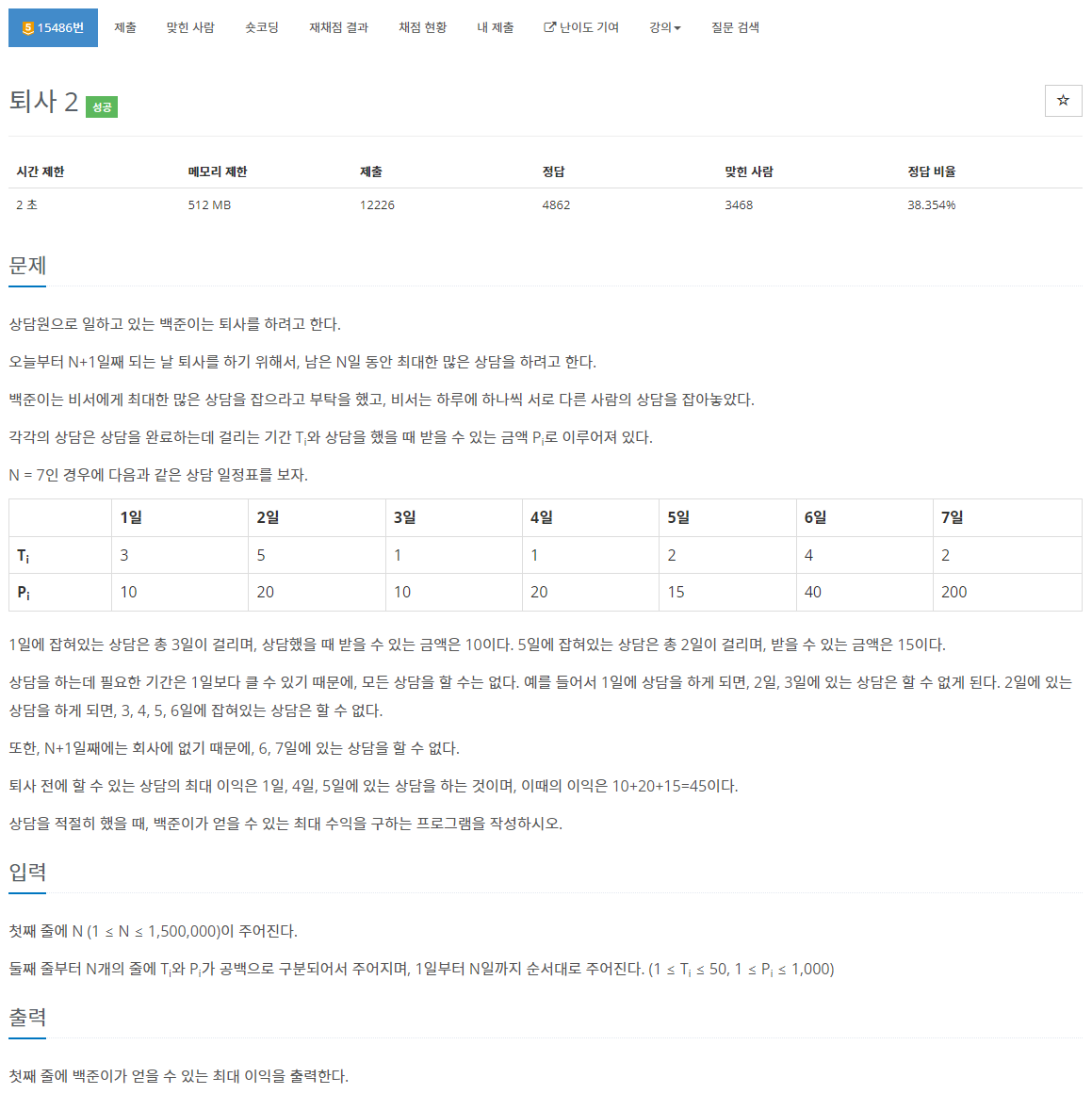
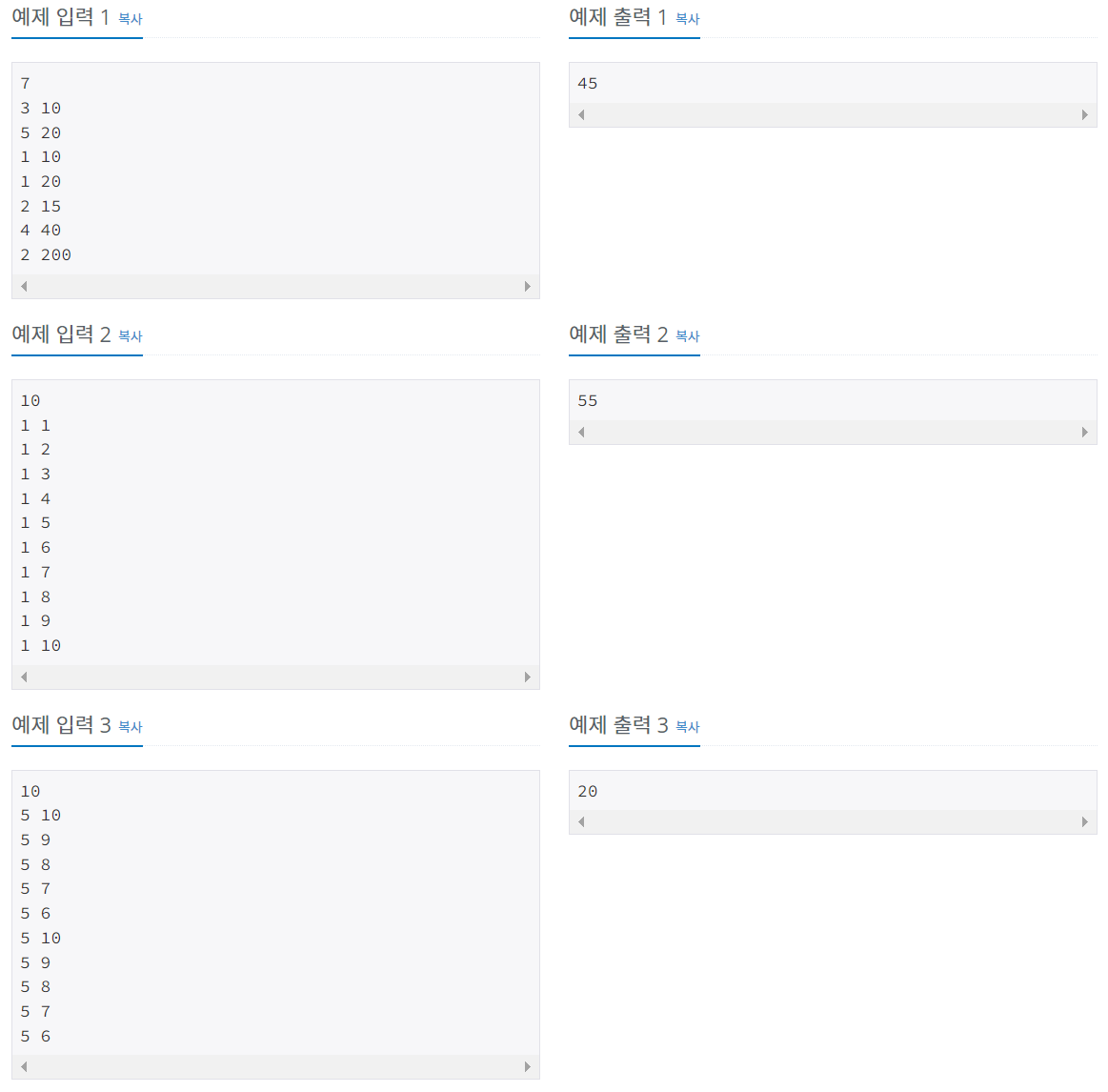퇴사 문제에서 N의 범위가 늘어나서 O(N^2) 풀이로는 풀 수 없었다. O(n)의 점화식을 도저히 생각해낼 수 없어 다른 사람의 풀이를 참고했다.
퇴사 1 풀이
- D[i] = i일의 상담을 할 때의 최대 수익
- D[i] = 상담하는 데 걸리는 시간 상 i일의 상담을 할 수 있는 D (1~i-1까지) 중 최댓값 + p[i]
O(n)의 접근법은 이렇다. 자기 이전의 D들로부터 얻어오는 것이 아니라, 모든 날짜에서 T[i]만큼 지난 날짜에 D[i] + P[i]를 때려넣는다. (최대일 때만)
퇴사2 풀이
- D[i] = i일에 이미 갖게 된 최대 수익 (당연히 i일 상담의 수익은 미포함)
- D[i+T[i]] = Math.max(D[i+T[i]], D[i] + P[i])
package dynamic;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ15486 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] T = new int[n + 1];
int[] P = new int[n + 1];
for (int i = 1; i < n + 1; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
T[i] = Integer.parseInt(st.nextToken());
P[i] = Integer.parseInt(st.nextToken());
}
int[] d = new int[n + 2];
int max = -1; //현재 검사한 날짜 중 최대 수익. 중간에 일을 하지 않는 날이 있으면 0인 원소가 생김 -> update
for (int i = 1; i < n + 1; i++) {
if (d[i] < max) d[i] = max;
else max = d[i];
if (i + T[i] > n + 1) continue;
d[i + T[i]] = Math.max(d[i + T[i]], d[i] + P[i]);
}
max = Math.max(max, d[n + 1]);
System.out.println(max);
}
}
주의할 점은 max 변수다. 단순히 최댓값을 저장하는 것 뿐 아니라, 이후의 d에 접근할 때마다 d가 max보다 작으면 갱신시켜줘야한다. d[i+T[i]]를 갱신하는 과정은 모든 날에 상담을 하는 경우만을 cover한다.
예를 들어, 5일에 상담이 끝난 뒤에, i=5의 상담을 바로 진행하는 경우 말고, 5일은 건너뛰고 6일의 상담을 진행하는 경우가 있을 수 있다. 하지만 상담은 5일에 끝났기 때문에 d[5]만이 갱신되고, 6일에 끝나는 상담이 존재하지 않기 때문에 d[6] = 0으로 남아있다. 6일에 이미 얻은 수익의 최댓값은 d[5]보다 크거나 같은 것이 당연한데도 말이다.
마지막으로 n일에 끝나는 일은 d[n+1]에 저장되므로, max와 비교해서 반환해준다.
5. 백준 9251 - LCS
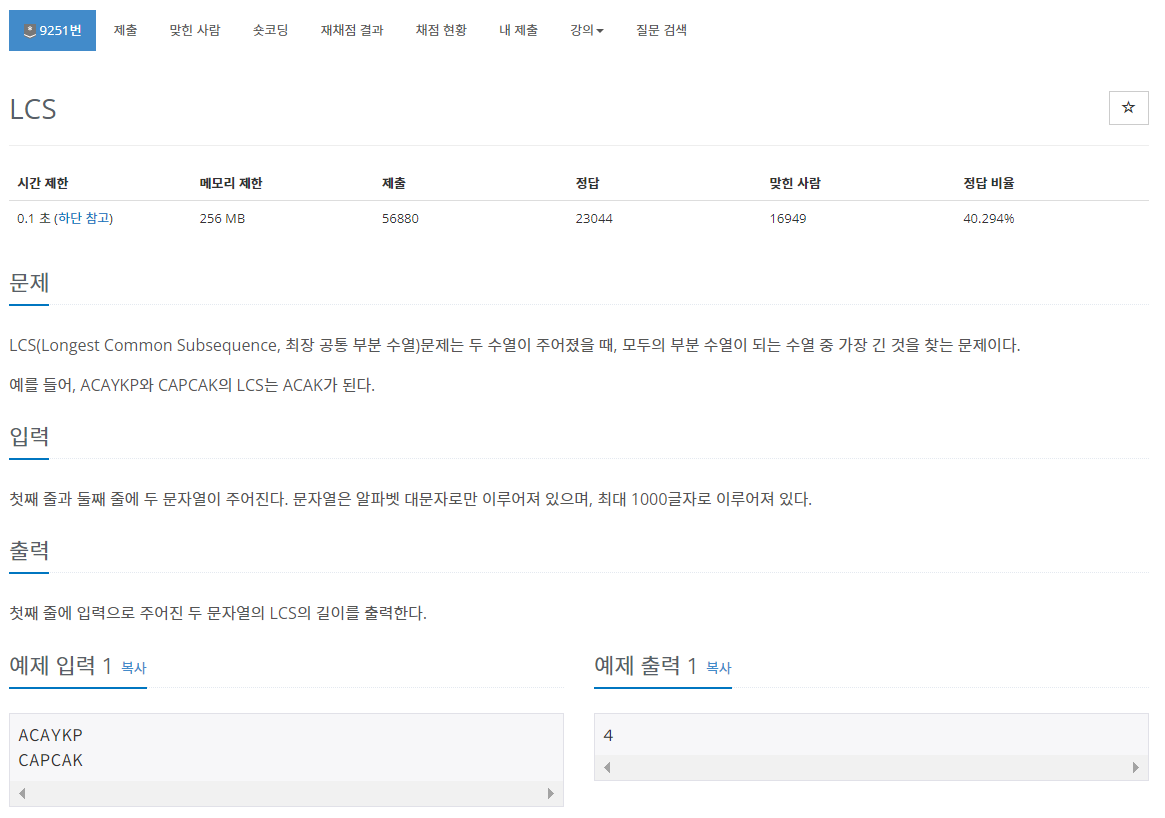풀이를 전혀 구상해내지 못했는데, 다른 풀이를 참고해 LCS 알고리즘을 확인하고 나니 처음 봤을 땐 못 푸는게 당연한 문제구나 싶었다.
LCS는 두 수열의 가장 긴 공동의 부분 수열을 의미한다.
배열의 정의는, D[i][j] = arr1의 0~i 배열과, arr2의 0~j 배열의 LCS이다. 직접 2차원 배열을 채워나가며 점화식을 유도해보니 이해가 됐다. 예제를 그려보고 점화식을 직접 유도하는 것이 dp를 푸는 데 정말 효과적인 방법이라고 느꼈다. 점화식은 다음과 같다.
- 문자 i, j가 같으면, D[i][j] = d[i-1][j-1] + 1
- 그렇지 않으면 d[i][j] = max(d[i-1][j], d[i][j-1]);
1번의 예를 들어보자면, ACA와 CAPCA에서 마지막 원소가 A로 같은 것을 확인했다. 그렇다면 ACA와 APCA의 LCS는, AC와 CAPC의 LCS에 하나의 공통원소가 추가된 것이다. 따라서 D[3][5] = D[2][4] + 1이 된다.
2번 조건 같은 경우는, ACA와 CAPC를 비교하고 나서 마지막 원소가 다른 것을 확인했다. 그렇다면 이전까지 구한 값 중에 최댓값을 취한다. AC와 CAPC, 또는 ACA와 CAP의 LCS가 ACA와 CAPC의 LCS가 될 것이다.
package dynamic;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.lang.reflect.Array;
import java.util.Arrays;
public class BOJ9251 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
char[] a = br.readLine().toCharArray();
char[] b = br.readLine().toCharArray();
int[][] d = new int[a.length + 1][b.length + 1];
for (int i = 1; i < a.length+1; i++) {
for (int j = 1; j < b.length+1; j++) {
if (a[i-1] == b[j-1]) {
d[i][j] = d[i - 1][j - 1] + 1;
} else {
//여긴 d[i-1][j]랑 d[i][j-1]중에 큰걸루 넣어야함.
//자기 이전의 수열들 사이의 경우의 수는 모두 포함하기 때무넹
d[i][j] = Math.max(d[i - 1][j], d[i][j - 1]);
}
}
}
for (int i = 0; i < d.length; i++) {
System.out.println(Arrays.toString(d[i]));
}
}
}
6. 백준 9084 - 동전
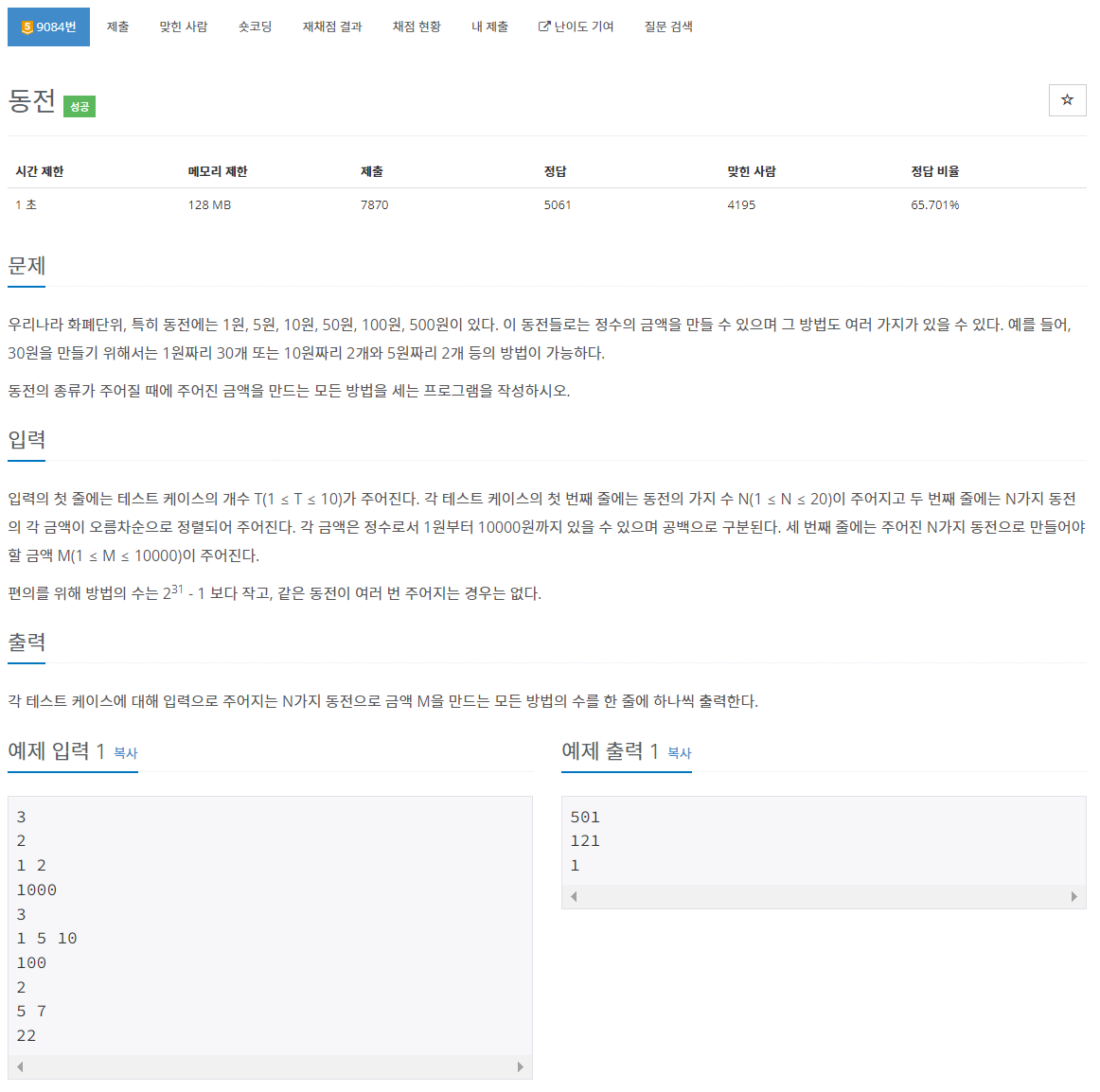처음에 접근한 풀이는, 배열 D[i] = i원을 만드는 동전 조합의 수로 설정하고, 모든 동전에 대해서 D[i] += D[i-coin]했다. 하지만 점화식을 이렇게 세우면, 조합이 아니라 순열을 얻게 된다는 것을 깨달았다.
예를 들어, 동전의 종류가 2, 3인 상태에서 D[5]를 구한다고 할 때, D[5] += D[2] + D[3]이 되는데, 이것은 2+3과, 3+2 두 개의 과정을 모두 포함한다. -> 조합이 아니다.
이것의 해법은, D[i]의 i가 아닌, 동전을 중심으로 쌓아올리는 방식으로 푸는 것이다.
- D[i] = i원을 만드는 동전 조합의 수
- 모든 coin에 대해서, D[i] = D[i-coin] (coin <= i < money + 1)
이렇게 동전을 중심으로 D에 경우의 수를 쌓아나가면 해당 동전의 개수가 의도된대로 더해진다.
package dynamic;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ9084_2 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
for (int i = 0; i < t; i++) {
int n = Integer.parseInt(br.readLine());
int[] coins = new int[n];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < n; j++) {
coins[j] = Integer.parseInt(st.nextToken());
}
int money = Integer.parseInt(br.readLine());
int[] d = new int[money + 1]; // d[i] = i원을 만드는 동전의 조합 수
d[0] = 1;
// for (int coin : coins) {
// d[coin]++;
// }
//이 방법은 coin부터 더하니까 coin 이전의 숫자들에 coin을 더하는 계산이 누락됨.
// for (int coin : coins) {
// if (coin > money) continue;
// d[coin]++;
// for (int j = coin; j + coin < money+1; j++) {
// d[j + coin] += d[j]; //j를 만드는 조합에다가 coin을 추가 -> 이러면 저번 풀이랑 똑같잖아..
// }
// System.out.println(Arrays.toString(d));
// }
for (int coin : coins) {
for (int j = coin; j < money + 1; j++) {
d[j] += d[j - coin];
}
}
System.out.println(d[money]);
// System.out.println(Arrays.toString(d));
}
}
}d[0]이 1이 되어야하는 이유는 d[j-coin]을 참조하기 때문에 초기값을 잡아줄 필요가 있기 때문이다.
끝
DP는 다른 알고리즘들에 비해서 많이 어려웠던 것 같다. 문제를 풀면서 느낀 가장 중요한 점은,
- 작은 스케일로 그려보는 과정이 정말 중요하다. 간단한 테스트케이스를 직접 그리고, 배열 D를 채워가면서 점화식을 유도해내는 것이 정말 좋은 방법이다.
- 그냥 엄청나게 풀어봐야한다. 연습문제를 풀 때야 DP 문제라는 것을 알고 들어갔기 때문에 접근 자체가 어렵진 않았다. DP를 이용한 풀이가 필요하다는 사실을 몰랐으면 접근이 많이 어려웠을 것 같다. 많이 풀어보면서, 메모이제이션과 점화식을 활용한 풀이가 필요한 지 잘 판단해내야할 것 같다.
연습문제 출처 : Encrypted-def github
