처음
탐색 알고리즘인 백트래킹을 공부했다. 백트래킹의 정의는, 현재 상태에서 가능한 모든 후보군을 따라 들어가며 탐색하는 알고리즘이다. BFS는 그래프에서 계층별로 탐색했다면, 백트래킹은 DFS와 비슷한 느낌으로 탐색한다고 이해했다.
백트래킹 역시 DFS와 BFS처럼 경우의 수를 모두 구하는 데 쓰일 수 있지만, 바둑/체스와 같은 게임이나 순열/조합 등을 계산할 때 많이 쓰일 것 같다.
중간
1. 백준 15649 - N과 M (1)
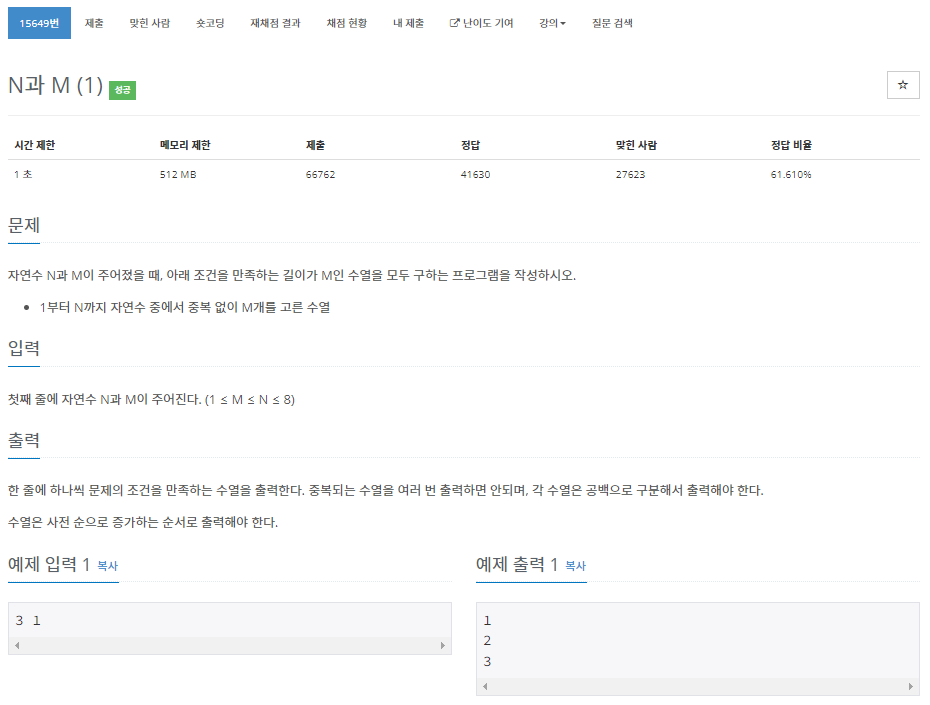
N과 M 문제는 백준에 열 두개 정도의 파생 문제가 있다. 모두 조합/순열 등과 관련된 문제인데, 백트래킹의 동작 원리를 이해하고 익숙해지는 데 많은 도움이 된다. 문제가 너무 많아 N과 M 문제들만을 다루는 포스팅을 따로 올려야겠다.
1부터 N까지의 수 중에서 M개의 조합 (nCm의 경우의 수)를 모두 구하는 문제다. 백트래킹이나 재귀를 모르고 문제를 접했다면 아마 N중 for문을 가장 먼저 떠올렸을 것 같다. 백트래킹을 활용하면 훨씬 간결한 코드로 해결할 수 있다.
package backtrack;
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ15649 {
static int[] arr;
static boolean[] isUsed;
static int m;
static int n;
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
arr = new int[n + 1];
for (int i = 1; i < n+1; i++) {
arr[i] = i;
}
isUsed = new boolean[n+1];
nandm(0);
bw.close();
}
private static void nandm(int k) throws IOException{
if (k == m) {
for (int i = 1; i < k+1; i++) {
bw.write(arr[i] + " ");
}
bw.newLine();
return;
}
for (int i = 1; i < n+1; i++) {
if (!isUsed[i]) {
isUsed[i] = true;
arr[k+1] = i;
nandm(k + 1);
isUsed[i] = false;
}
}
}
}
백트래킹의 핵심은 nandm 함수의 for문이라고 할 수 있다. k는 DFS에서의 depth와 비슷한 기능을 한다고 보면 된다. isUsed[n]은 n이 이번 탐색에서 이미 사용됐는지를 확인하기 위한 배열이다. 조합에서는 원소가 중복되면 안되기 때문에, 지금 검사하는 값을 사용하지 못하게 만든 다음, 다음 depth로 넘어간다. 재귀를 지난 번에 공부했기 때문에 이 로직을 받아들이기 어렵진 않았다.
2. 백준 9663 - N-Queen
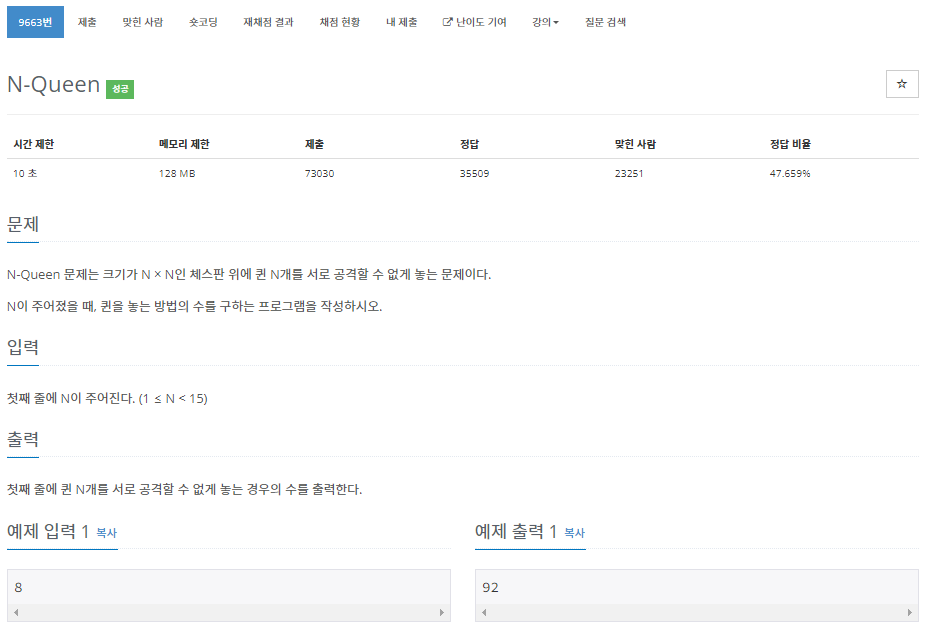나는 몰랐지만, 문제 풀이 후 다른 사람들의 포스트를 보면서 이 문제가 백트래킹의 대표 예제라는 것을 알게 됐다. 문제를 처음 접했을 때는, n*n 배열을 전부 검사하면서 모든 경우의 수를 확인했다. O(n^2)에다가 놓여진 퀸끼리의 위치 비교를 위한 list를 사용했고, 재귀는 메서드 호출 때문에 메모리와 시간도 많이 잡아먹기 때문에 메모리/시간 초과가 떴다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
class Pair {
int x;
int y;
public Pair(int x, int y) {
this.x = x;
this.y = y;
}
}
public class Main {
static int n;
static int cnt = 0;
static List<Pair> tmpQueens;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
tmpQueens = new ArrayList<>();
nQueen2(0);
System.out.println(cnt);
}
private static void nQueen2(int k) {
if (k == n) {
cnt++;
return;
}
a : for (int j = 0; j < n; j++) {
for (Pair old : tmpQueens) if (prohibited(old, k, j)) continue a;
tmpQueens.add(new Pair(k, j));
nQueen2(k + 1);
tmpQueens.remove(tmpQueens.size() - 1);
}
}
private static boolean prohibited(Pair old, int x, int y) {
if (old.x == x || old.y == y || Math.abs(old.x - x) == Math.abs(old.y - y)) {
return true;
}
return false;
}
}
그 다음에 생각한 해결책은, 퀸의 상하좌우 대각선에는 둘 수 없기 때문에, 각 행마다 오직 하나의 퀸을 둘 수 있다는 점을 활용하는 것이었다. 매번 검사의 대상이 되는 케이스가 n개 밖에 되지 않고 조건도 더 적어졌다.
package backtrack;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
//2중 for문으로 싹다 검사하면서 List에 좌표 정보 (pair)를 저장하는 방식 -> 시간, 메모리 모두 초과
//같은행에는 어차피 두개 존재할 수 없기 떄문에, 행별로 하나씩 arr에 저장하는 방식. list와 pair를 쓸 필요도 없고 탐색 시간도 훨씬적다
public class BOJ9663 {
static int[] tmpQueens;
static int n;
static int cnt = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
tmpQueens = new int[n];
nQueen2(0);
System.out.println(cnt);
}
private static void nQueen2(int k) {
if (k == n) {
cnt++;
return;
}
a : for (int j = 0; j < n; j++) {
//list -> arr 로 바꾸고, 어차피 행마다 검사하니까 Pair -> int로 바꿈
//prohibited 검사할 때는, 값이 같은지와, 값의 차가 인덱스의 차와 같은지 확인
for (int i = 0; i < k; i++) {
if (tmpQueens[i] == j || Math.abs(tmpQueens[i] - j) == k - i) continue a;
}
tmpQueens[k] = j;
nQueen2(k + 1);
}
}
}
지금 확인하는 좌표가 tmpQueens에 있는 퀸들과 같이 존재할 수 있는 지 확인할 때는 현재 좌표가 (k, i)라는 점을 이용해서 tmpQueens[i]와 비교했다.
3. 백준 1182 - 부분수열의 합
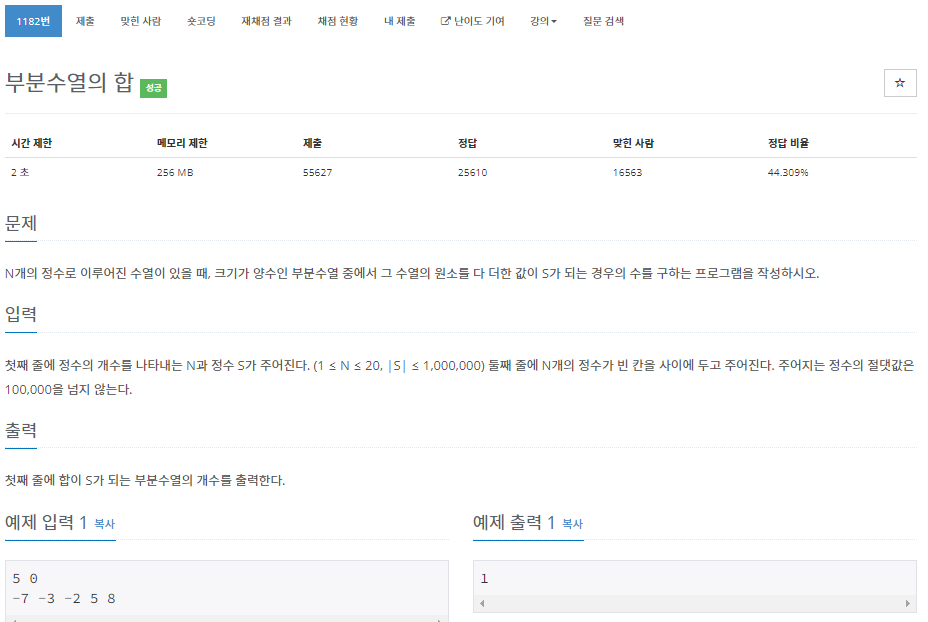
첫 번째 n과 m 문제와 같이 중복 없이 조합을 구하는 문제였다.
이번엔 수열이 아닌 수열의 합을 구해야하는 것이었으므로 함수에 수열의 합을 나타내는 인자를 추가했고, 공집합을 제외하기 위해 공집합 여부를 확인하는 boolean 변수를 추가했다.
package backtrack;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BOJ1182 {
static int[] arr;
static int n;
static int cnt;
static int s;
static boolean[] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
s = Integer.parseInt(st.nextToken());
arr = new int[n];
visited = new boolean[n];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
backTrack(0, 0, true);
System.out.println(cnt);
}
private static void backTrack(int k, int sum, boolean gong) {
if (k == n) {
if (sum == s && !gong) {
cnt++;
}
return;
}
backTrack(k+1, sum, gong);
backTrack(k+1, sum+arr[k], false);
}
}
끝
백트래킹은 dfs와 재귀 공부의 연장선상 느낌이라 생각보다 개념을 받아들이고 적용하는 데 큰 어려움이 있진 않았다. 다음 포스트에서는 백트래킹 연습 문제은 N과 M 문제를 모두 풀고 복습할 것이다.
연습문제 출처 : encrypted-def github
