처음
이번에는 재귀(recursion)에 대해서 공부했다. 고등학교 수학을 하면서 재귀, 귀납 등에 대해 들어봤기 때문에, 정확히는 아니더라도 그 느낌이라던가, 쓰임에 대해서는 잘 알고 있었다.
재귀 라는 말의 정의는, 무언가를 정의하는 과정에서 자기 자신을 참조하는 것을 말한다. 재귀라는 개념 자체가 직관적으로 와닿긴 힘들지만 정의라던가, 참조 같은 단어들을 이용해 설명되기 때문에 뭔가 프로그래밍에서 어떻게 쓰이는 것인지 감을 잡기는 쉬울 것이라고 생각한다. 후려쳐서 설명하면, 메서드에서 자기 자신을 다시 호출하면, 그게 바로 재귀이고 그 메서드는 재귀 함수인 것이다.
재귀의 개념은 DFS와 백트래킹 등, 알고리즘 문제를 해결하는 데 아주 유용하게 쓰인다. 재귀의 개념을 적용할 때는 그 장단점이 확실하다. 예를 들어 어떠한 탐색에서, 반복문 등의 방법으로 모든 경우의 수를 확인하는 등의 방법 (일종의 hard cording)이 아니라, 우리의 목적인 탐색에서 어떤 귀납적인 규칙을 찾아내어 재귀 함수를 구현하면 더 간결하고 깔끔하게 코드를 짤 수 있다. 하지만 반면에 탐색을 하는 경우의 수는 똑같고 함수 호출은 매우 많아지기 때문에 메모리/시간 측면에서는 손해를 본다. 그래서 백트래킹이나 DFS를 활용하는 문제는 시간 제한과 메모리 제한을 잘 확인해야 한다.
재귀를 활용한 연습 문제들을 풀어보면서 내가 느낀 것은, 재귀 함수를 활용해서 문제를 해결하는 능력은 결국 귀납적 사고력에 의해서 결정된다는 것이다. 처음부터 백날 글로 설명해봐야 절대 이해할 수 없는 개념이기 때문에, 연습 문제들을 확인해보자.
중간
1. 백준 1629번 - 곱셈
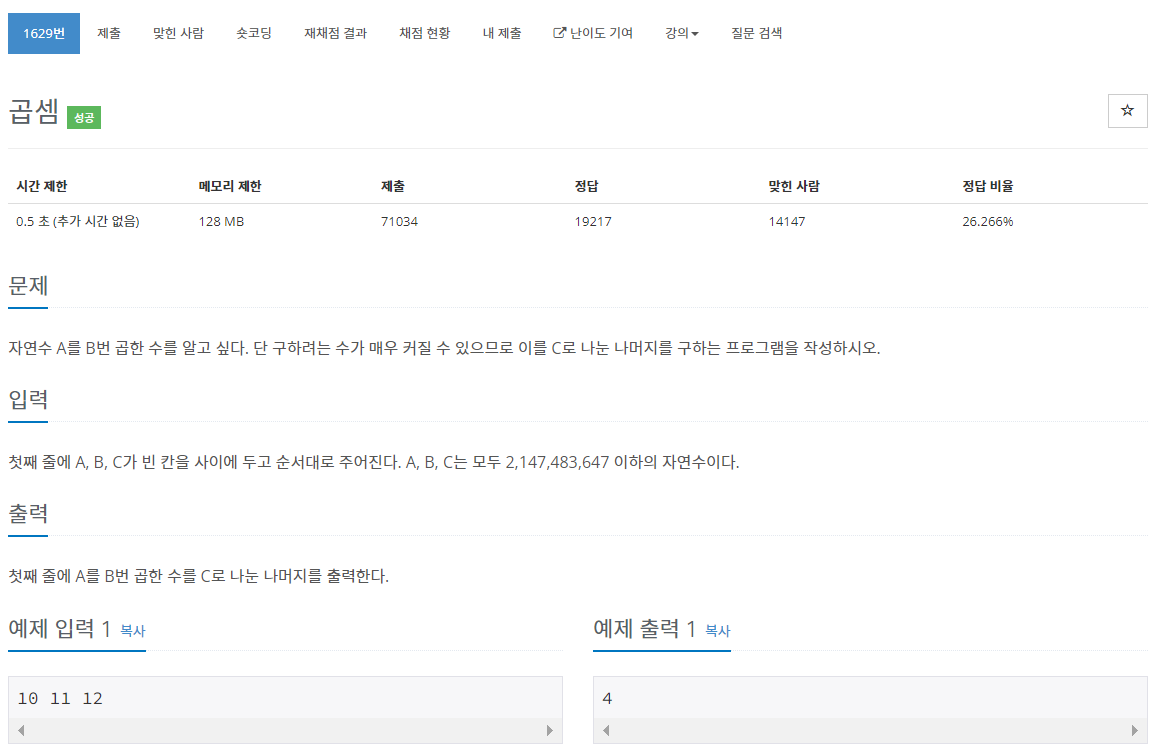
정말 간단해보이지만, 이 문제의 함정은 정수의 범위가 너무 넓어서 A^B를 하는 과정에서 어떤 정수 자료형을 써도 오버플로우가 날 수 있다는 것이다. 그럼 A를 직접 B번 곱한 뒤에 C로 나누는 것 말고 다른 방법이 필요하다.
A^B는 A*A*A*....*A의 형태로 표현할 수 있다. 그리고 A^n을 C로 나눈 나머지는, A^(n/2)를 C로 나눈 나머지를 두 번 더한 것과 같다. 이것이 직관적으로 이해하기 위해서는, 매우 큰 수를 10으로 나눈 나머지를 구하는 예시를 생각해보면 된다. 29481 * 1298412 * 1236를 10으로 나눈 나머지를 구하라고 한다면, 당연히 각 숫자의 1의자리인 1, 2, 6을 곱하는 방법을 이용할 것이다. 지금 문제에서의 차이는 10에서 C로 바뀐 것 뿐이다.
그렇다면 이제 문제는, A^B를 여러 개로 쪼개서, 쪼갠 조각들에 대해서 C로 나누고 다시 곱하는 과정을 반복하기만 하면 된다. 그리고 이 과정을 재귀를 활용해서 아주 깔끔하게 표현해낼 수 있다.
A^B를 (A^(B-1)를 C로 나눈 나머지) * (A를 C로 나눈 나머지)로 표현한다면, 왼쪽의 (A^(B-1)를 C로 나눈 나머지)도 다시 쪼개질 수 있다. : (A^(B-2)를 C로 나눈 나머지) * (A를 C로 나눈 나머지))
또는 반으로 쪼개 (A^(B/2)를 C로 나눈 나머지) * 2로 표현할 수도 있을 것이다. 그리고 이 과정 역시 A를 C로 나눈 나머지로 쪼개질 때 까지 반복될 수 있다. 이것을 귀납적으로 표현한다면, A^k를 계산할 수 있다면, A^(k/2)도 계산할 수 있기 때문에, 재귀 함수를 활용해서 해결할 수 있다 라고 말할 수 있는 것이다. 특정 값의 거듭제곱을 나눈 나머지를 구하는 함수를 만들어서, 재귀적으로 호출하면 된다. 코드를 확인해보자.
public class BOJ1629 {
static long C;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
long a = Integer.parseInt(st.nextToken());
long b = Integer.parseInt(st.nextToken());
long c = Integer.parseInt(st.nextToken());
C = c;
System.out.println(recursive(a,b,c));
}
private static long recursive(long a, long b, long c) {
if (b == 1) return a % c;
long val = recursive(a, b/2, c);
if (b%2 == 1) return (val * val % c) * a % c;
return val * val % c;
}
}val이라는 변수에, 현재 메서드의 b를 반으로 쪼개서 실행한 메서드의 결과를 담았다.
그리고 이 반으로 쪼갠 값의 나머지를 구하는 식으로 구현됐다.
여기서 val이라는 함수는, A를 B/2로 나눈 나머지라고 해석해야한다. 또 추가적으로 b가 나누어떨어지지 않는 경우에는 a를 c로 나눈 나머지를 한 번 더 곱해주었다.
또 재귀함수에서 정말 중요한 부분은 메서드 첫 줄의 if문이다. 이것을 base condition이라고 하는데, 마지막 단계를 정해주지 않는다면 재귀함수는 무한히 실행될 것이기 때문에, 하한을 정해준다. 그리고 그 하한은, A^B가 최대로 쪼개진 상태인, b가 1인 경우다. 이때는 그냥 a를 c로 나눈 나머지를 반환한다.
정리하자면, 재귀 함수를 구현할 때 핵심은 다음의 세 가지이다.
- base condition : 재귀 함수의 하한. 가장 아랫 단계의 정의 : 위 문제에서는 b==1 일 때, a%c를 반환한다. (recursive는 a^b를 c로 나눈 나머지를 반환하는 함수니까)
- 함수의 정의 : 재귀 함수가 무엇을 인자로 받아 무엇을 반환하는 지 확실히 해야한다. : 위의 recursive는 a, b, c를 인자로 받아 a^b를 c로 나눈 나머지를 반환하는 함수다.)
- 재귀 식 (메서드의 return 부분) : recursive(a, b/2, c)를 두 번 곱해 c로 나눈 값을 반환한다.
이 세 가지를 고려해서 함수를 구현해야 한다.
2. 백준 11729 - 하노이 탑 이동 순서
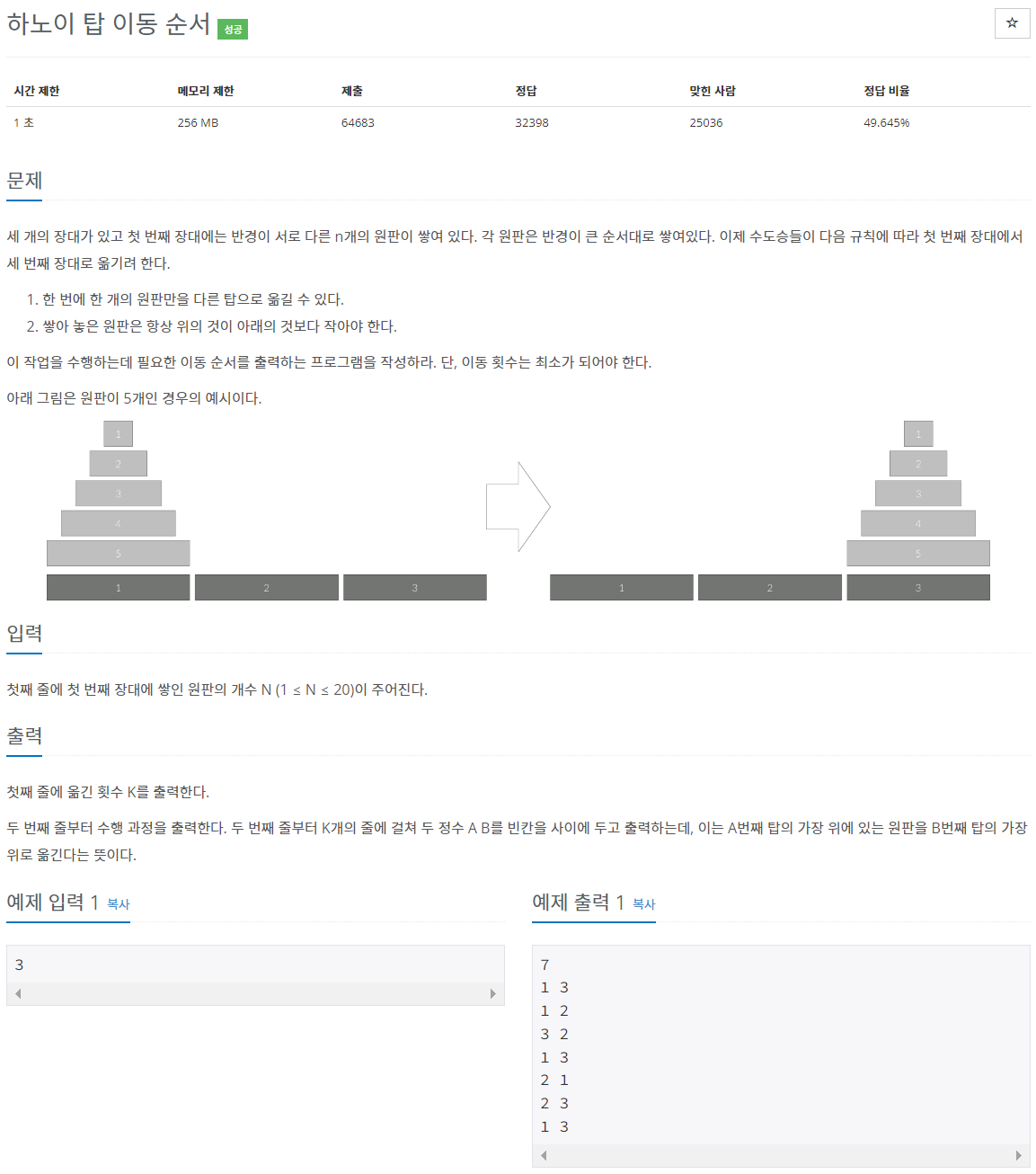
재귀 함수의 대표적인 예제인 하노이 탑 이동 순서이다. 이 문제의 귀납적인 해결책을 발견하기 위해서는 직접 문제를 풀어보는 과정이 필요하다. 꼭 직접 해보길 바란다.
정답부터 말하자면, n개의 하노이의 탑을 3번으로 옮기기 위해서는 1)마지막 판을 제외한 n-1개의 판을 2번으로 옮긴다. 2) 마지막 n번째 판을 3번으로 옮긴다. 3)2번의 n-1개의 판을 3번으로 옮긴다. 의 과정이 필요하다. 그리고 이 과정(특정한 위치로 판들을 옮기는 과정)은 1<= k <= n인 k에 대해서 모두 적용될 수 있다. 감이 좀 잡히는가? 귀납적으로 반복되어야 하는 과정이 k개의 판을 어떤 위치에서 다른 위치로 옮기는 것이다. 그렇다면 우리가 만드는 재귀함수의 기능은 바로 이것이 되어야한다.
package recursion;
import java.io.*;
import java.util.ArrayList;
import java.util.List;
public class BOJ11729 {
static List<String> list;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
list = new ArrayList<>();
hanoiTower(n, 1, 3);
bw.write(list.size()+"");
bw.newLine();
for (String x : list) {
bw.write(x);
bw.newLine();
}
bw.close();
}
private static void hanoiTower(int n, int start, int target) {
if (n == 1) {
list.add(start + " " + target);
// System.out.println(start + " " + target);
return;
}
//n-1개의 탑을 2번으로 옮김
hanoiTower(n-1, start, 6-start-target);
//n번째 원판을 3번으로 옮김
hanoiTower(1, start, target);
// 2번의 n-1개 탑을 3번으로 옮김
hanoiTower(n-1, 6-start-target, target);
}
}
함수의 선언부는 위에서 우리가 함수를 정의한 것처럼, 인자는 옮길 판의 개수 n과, 현재 위치인 start와, 옮기길 원하는 위치인 target 세 가지이다. 아래의 함수를 재귀적으로 호출하는 부분의 6-start-target은, start와 target 외의 다른 위치 (start=1, target=3이라면 2)를 나타낸다.
그리고 여기서 호출된 함수들도 똑같은 과정을 거치면서, 결국엔 base condition인 n==1로 다다를 것이다. n==1이 의미하는 것은, 한 개의 판을 옮긴다는 것이다. 하나의 판을 옮기는 과정은 더 쪼갤 필요 없이 이동하는 위치를 출력하기만 하면 된다. 옮기는 순서를 출력하기만 하면 되기 때문에 반환값은 없다.
재귀 함수를 처음 접하면 직관적으로 이해하기 힘들 것이다. 하지만 재귀를 이용하기 위해서는 절차지향적인 사고를 버리고, 귀납적으로만 사고해야한다. 위에서 이야기한 세 가지 핵심을 고려해 함수를 구현하면, 다른 단계에서도 똑같은 과정이 일어날 것이라는 생각 정도만이 필요한 것 같다. 이것 또한 연습을 통해 익숙해지는 것 같다.
3. 백준 1074 - Z
재귀를 공부하면서 접한 문제였기 때문에 n을 반으로 쪼개가면서 재참조해서 어떻게 잘 하면 해결할 수 있을 것이라는 생각 정도가 먼저 들었다.
private static void z(int row, int col, int n) { //row, col은 시작 좌표
if (finished) return;
if (n == 1) {
cnt++;
if (row == r+1 && col == c+1) {
System.out.println(--cnt);
finished = true;
return;
}
// System.out.println(row + " " + col);
return;
}
z(row, col, n / 2);
z(row, col + n / 2, n / 2);
z(row + n / 2, col, n / 2);
z(row + n / 2, col + n / 2, n / 2);
}내가 첫 번째로 생각해낸 풀이다. 배열을 탐색하는 순서가 n/2로 쪼갠 네 개의 정사각형에 대해 왼쪽 위, 오른쪽 위, 왼쪽 아래, 오른쪽 아래 이기 때문에 n에 대해서 각각의 사분면에 대해 z를 호출했다. 이 함수의 정의는, 2^n * 2^n 배열을 z자로 탐색하는 함수인 것이다. 그러다 base condition인 n==1에 도달했다는 것은, 비로소 특정한 좌표를 정해진 순서대로 탐색했다는 것이고, 그래서 cnt를 더하고 우리의 목적인 좌표와 같은지 확인했다.
하지만 이 방법은 r,c 이전의 모든 원소를 직접 탐색해야하는 방법이었기 때문에 역시나 시간 초과가 떴다.
그래서 강좌 블로그의 풀이를 참고했다. (해당 블로그는 C++을 사용한다.)
private static int z2(int r, int c, int n) {
if (n == 1) return 0;
int half = n/2;
if (r >= half && c >= half) return 3 * half * half + z2(r - half, c - half, n / 2);
else if (r < half && c >= half) return half * half + z2(r, c - half, n / 2);
else if (r < half && c < half) return z2(r, c, n / 2);
else return 2 * half * half + z2(r - half, c, n / 2);
}나의 풀이는 (0,0)부터 문제의 탐색 방법을 그대로 따라가는 방식이었다면, 이 풀이는 입력받은 r, c가 배열의 몇번 째 사분면에 위치하는지를 확인해 탐색 범위를 줄여나가는 방식이었다. 네 개의 (n/2) * (n/2) 정사각형으로 쪼개면, 이 각각의 정사각형에서 이동한 거리는 (n/2)*2이 된다는 점에 주목해야한다.
예를 들어, r,c가 3사분면에 있다면, 1, 2사분면을 탐색할 필요 없이 (n/2)\^2을 두번 곱한 값 만큼을 이미 이동했다고 생각하면 되는 것이다.
4. 백준 17478 - 재귀함수가 뭔가요?
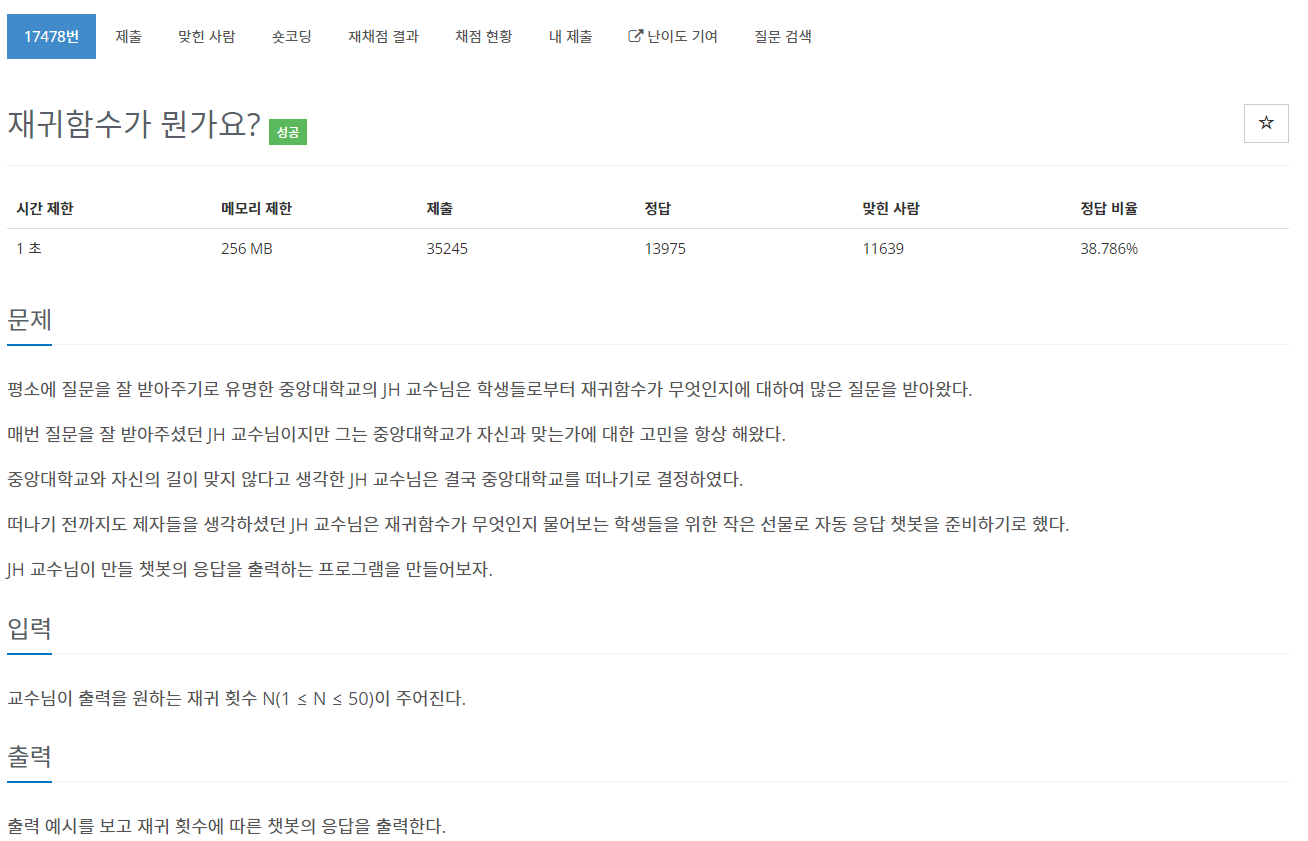
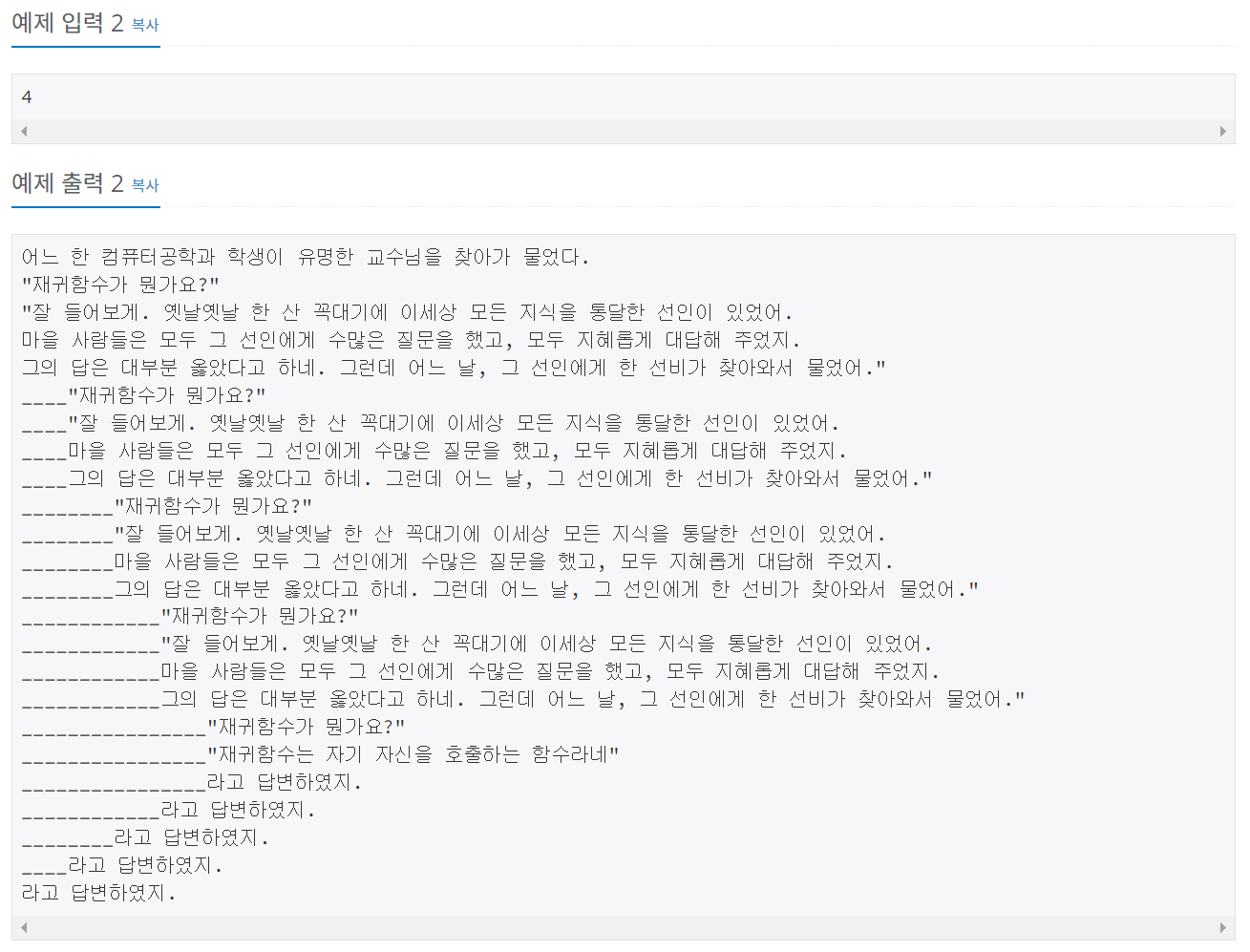위의 문제들과 달리 재귀를 어떻게 적용해야할 지 쉽게 파악할 수 있는 문제였다.
package recursion;
import java.io.*;
public class BOJ17478 {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static String[] advice = {"\"재귀함수가 뭔가요?\"", "\"잘 들어보게. 옛날옛날 한 산 꼭대기에 이세상 모든 지식을 통달한 선인이 있었어."
, "마을 사람들은 모두 그 선인에게 수많은 질문을 했고, 모두 지혜롭게 대답해 주었지.", "그의 답은 대부분 옳았다고 하네. 그런데 어느 날, 그 선인에게 한 선비가 찾아와서 물었어.\""};
static int N;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
bw.write("어느 한 컴퓨터공학과 학생이 유명한 교수님을 찾아가 물었다.");
bw.newLine();
doctorSays(0);
bw.close();
}
private static void doctorSays(int n) throws IOException{
if (n == N) {
for (int j = 0; j < n; j++) {
bw.write("----");
}
bw.write("\"재귀함수가 뭔가요?\"");
bw.newLine();
for (int j = 0; j < n; j++) {
bw.write("____");
}
bw.write("\"재귀함수는 자기 자신을 호출하는 함수라네\"");
bw.newLine();
for (int j = 0; j < n; j++) {
bw.write("____");
}
bw.write("라고 답변하였지.");
return;
}
for (int i = 0; i < 4; i++) {
for (int j = 0; j < n; j++) {
bw.write("____");
}
bw.write(advice[i]);
bw.newLine();
}
doctorSays(n+1);
bw.newLine();
for (int i = 0; i < n; i++) {
bw.write("____");
}
bw.write("라고 답변하였지.");
}
}
함수의 정의는 정해진 구문(재귀함수가 뭔가요~~어쩌구)를 출력하는 함수 정도가 될 것 같다. 물론 그냥 반복적으로 출력하는 것이 전부이기 때문에 이런 정의도 딱히 필요없다고 생각한다. 반복적으로, 순서대로 출력해야하는 문자열들은 배열에 담아 코드를 간결하게 했다.
5. 백준 1780 - 종이의 개수
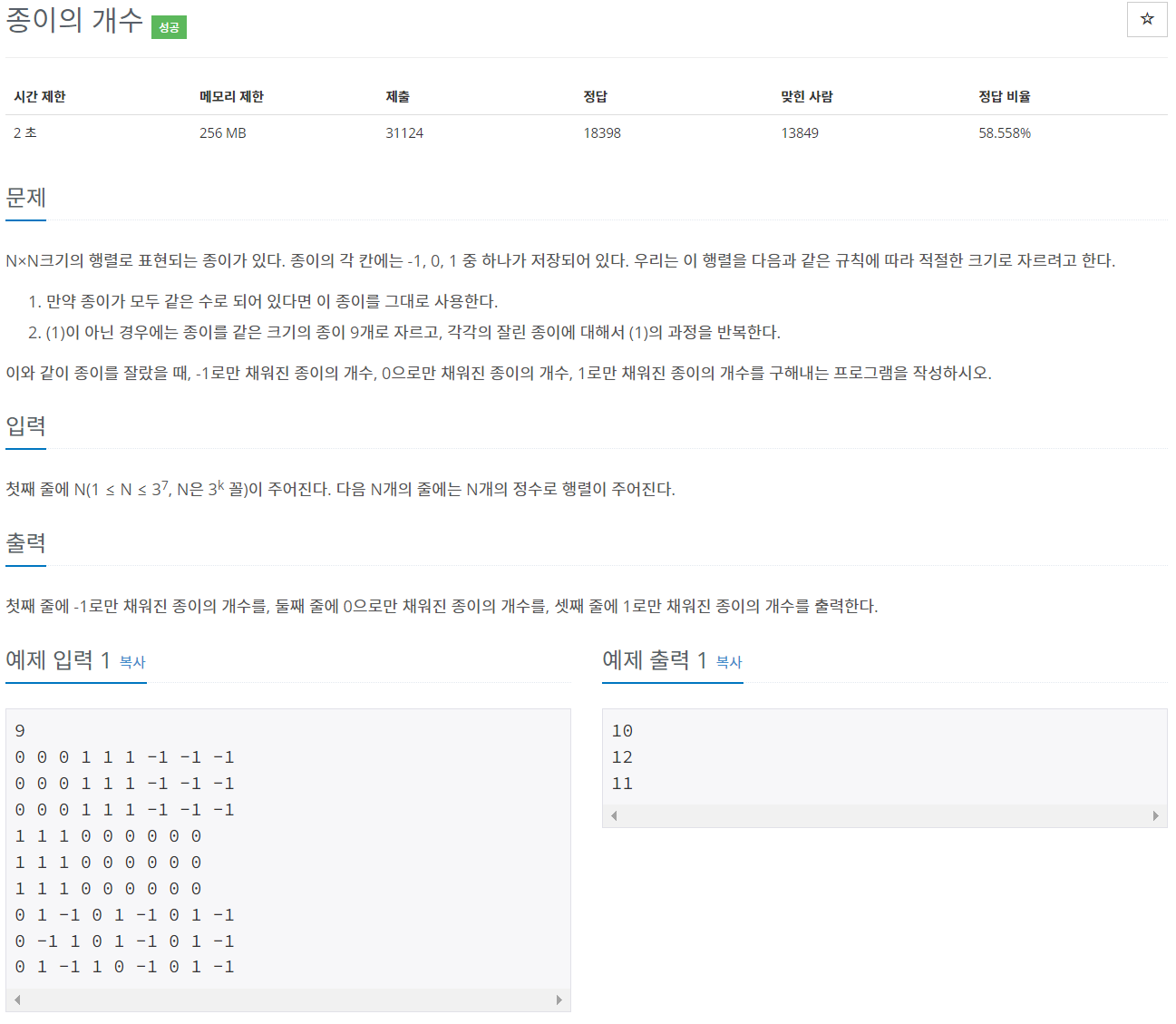
종이를 일정한 규칙으로 잘라가며 검사하는 과정이 필요하다고 명시했기 때문에 재귀를 이용하는 것이 당연했다.
함수는 문제에서 설명해준대로 구현했다. 찾는 종이 (1, -1, 0)을 따로 구현했고, n/3의 종이들이 모두 같다면, 1을, 그렇지 않다면 그냥 찾는 종이의 개수를 반환하도록 했다.
package recursion;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
//https://ideone.com/F0uTwN 반례 참고 -> 근데 답 6 10 9임
//그냥 n= N부터 시작해서 매번 모든 격자 check할 수도 있을 듯
public class BOJ1780 {
static int answer = 0;
static int N;
static int[][] paper;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
paper = new int[N][N];
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
paper[i][j] = Integer.parseInt(st.nextToken());
}
}
System.out.println(paper0(0, 0, N, -1));
System.out.println(paper0(0, 0, N, 0));
System.out.println(paper0(0, 0, N, 1));
}
private static int paper0(int x, int y, int n, int target) {
if (n == 1) {
if (paper[x][y] == target) return -1;
return 0;
}
int answer = 0;
int isUnified = 0;
//검사하는 영역이 unified면 -1 리턴
//그 다음 단계에서는 합이 -9이면 1 리턴
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
int tmp = paper0(x + n/3 * i, y + n/3 * j, n/3, target);
if (tmp == -1) isUnified++;
answer += tmp;
}
}
if (answer == -9) {
if (N == n) {
return 1;
}
return -1;
}
return answer + 2*isUnified; // -7 + 16 = 9
}
}
함수는 아래 단계의 종이 개수들을 더해 현재 단계의 종이 개수를 반환하는 함수다. base condition은 당연히 n==1일 때 이고, 해당 종이가 우리가 찾는 종류이면 -1을 반환한다. 그렇기 때문에 다음 단계에서 받은 종이의 개수가 -9라면, 하나의 종이인 것이므로, 다음 단계에 -1를 반환한다.
왜 1과 9가 아닌 -1, -9가 나와야 하냐면, 해당하는 종이를 1로 표시한다면, 그냥 해당 종이에 찾는 종이 (1, -1, 0)이 하나 있는 것인지, 아님 하나의 종이인 것인지를 구분할 수 없기 때문이다. 예컨데
1 0 0
0 0 0
0 0 0
과
1 1 1
1 1 1
1 1 1
모두 1을 반환하기 때문이다. answer에 이 값을 저장하면, 두 경우를 구분할 수 없다. tmp가 모두 -1인 경우만이 unified, 즉 같은 종이임을 의미하기 때문에 -1를 return하고, 그렇지 않으면 그냥 종이의 개수(isUnified는 부호가 반대이기 때문에 2 곱해서 answer에 더해주면 구하는 값이 된다.)를 return한다.
6. 백준 2630 - 색종이 만들기
이전 문제와 매우 비슷하고, 쪼개는 개수도 네 개이기 때문에 더 간단하다.
이번에는 더 직관적인 방법으로, 각각의 단계에 대해서 직접 완전탐색해서 해결하는 방식으로 풀어봤다.
package recursion;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BOJ2630 {
static int[][] confetti;
static int[] answer = new int[2];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
confetti = new int[n][n];
for (int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < n; j++) {
confetti[i][j] = Integer.parseInt(st.nextToken());
}
}
confettiRecur(0,0,n);
System.out.println(answer[0]);
System.out.println(answer[1]);
}
private static void confettiRecur(int x, int y, int n) {
if (n == 1) {
answer[confetti[x][y]]++;
return;
}
int a = isUnified(x, y, n);
if (a != -1) {
answer[a]++;
return;
}
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
confettiRecur(x + i * n/2, y + j * n/2, n/2);
}
}
}
private static int isUnified(int x, int y, int n) {
int prev = confetti[x][y];
for (int i = x; i < x+n; i++) {
for (int j = y; j < y+n; j++) {
if (prev != confetti[i][j]) return -1;
}
}
return prev;
}
}
isUnified 함수는 해당 n*n이 하나의 종이인지 판단하는 함수다. 하나의 함수일 경우 0, 1 중에 하나를 반환하고 그렇지 않다면 -1을 반환한다.
재귀함수에서는 이 함수를 실행해서 0, 1이라면 answer 배열의 0, 1중 해당하는 값을 증가시킨다. 그렇지 않다면 네 개로 쪼갠 종이에 대해서 같은 과정을 반복한다.
base condition인 n==1까지 왔다면, 한 칸이 하나의 종이인 것이므로, answer에 각각 더해주면 되겠다.
7. 백준 1992 - 쿼드트리
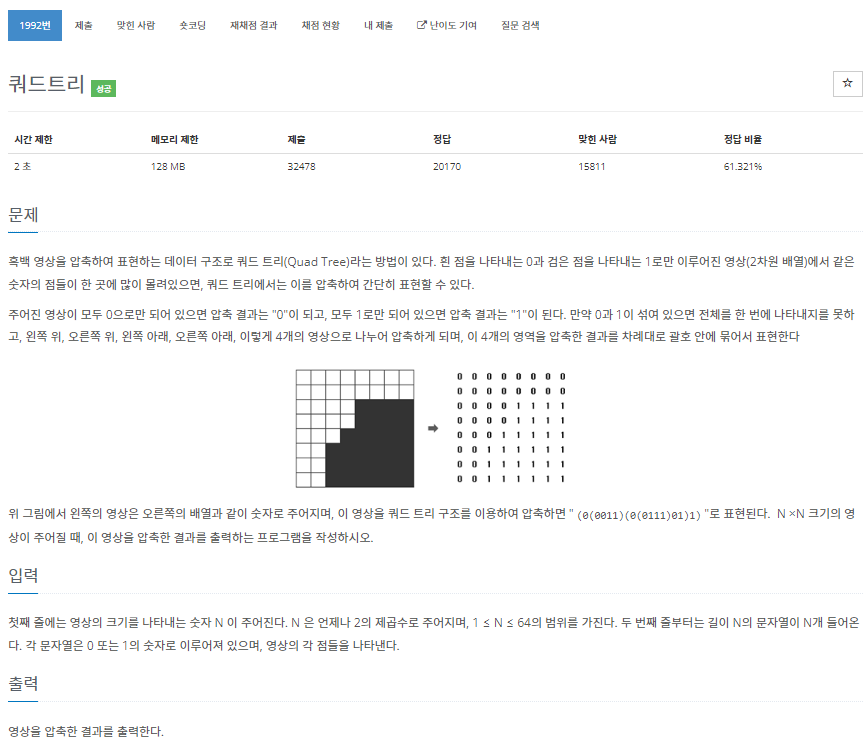
5, 6번 문제들을 풀고 나서 보니 해법이 너무 쉽게 보이는 문제였다.
package recursion;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BOJ1992 {
static int[][] image;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
image = new int[n][n];
for (int i = 0; i < n; i++) {
String[] a = br.readLine().split("");
for (int j = 0; j < n; j++) {
image[i][j] = Integer.parseInt(a[j]);
}
}
System.out.println(quadTree(0, 0, n));
}
private static String quadTree(int x, int y, int n) {
if (n == 1) {
return image[x][y]+"";
}
int a = isUnified(x, y, n);
if (a != -1) {
return a+"";
}
String answer = "";
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
answer += quadTree(x + n / 2 * i, y + n / 2 * j, n / 2);
}
}
return "(" + answer + ")";
}
private static int isUnified(int x, int y, int n) {
int prev = image[x][y];
for (int i = x; i < x+n; i++) {
for (int j = y; j < y+n; j++) {
if (prev != image[i][j]) return -1;
}
}
return prev;
}
}
정사각형을 네 등분해가며, 해당 부분이 같은 수로만 이루어져있는지 확인하면 된다. 다만 이전의 문제와 다른 점은 결과 출력의 방식이다. 재귀적으로 발생하는 네 개의 정사각형 영역들은 괄호로 묶여져있어야하므로, 해당 영역의 쿼드트리를 괄호로 감싸주면 되겠다.
그 외에는 이전 문제와 거의 같았다.
8. 백준 2447 - 별 찍기 - 10
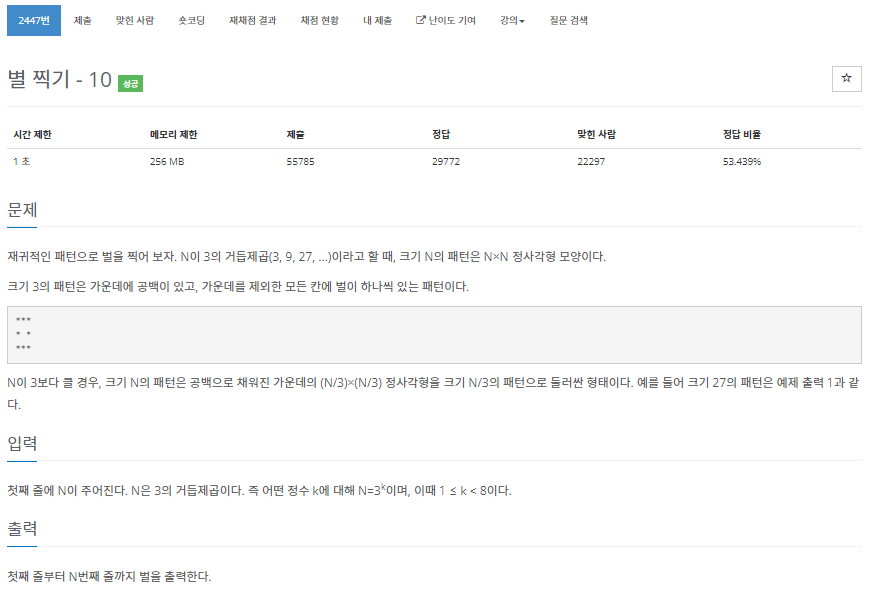보자마자 함수의 인자 n에 대해서 n/3을 인자로 넣는 방식의 재귀함수를 구현해야할 것이라는 생각이 들었다. 그리고, 모든 단계에서 가운데의 원소는 공백이어야하기 때문에 이것을 정할 boolean 변수를 따로 만들어줬다.
package recursion;
import java.io.*;
import java.util.Arrays;
import java.util.Scanner;
public class BOJ2447 {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static String[][] board;
static int[][] test;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
board = new String[n][n];
test = new int[n][n];
star(0, 0, n ,false);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
bw.write(board[i][j]);
}
bw.newLine();
}
bw.close();
}
//2차원배열로 해보까? n/3씩 해가믄스
private static void star(int x, int y, int n, boolean blank) {
if (n == 1) {
if (blank) {
board[x][y] = " ";
}
else board[x][y] = "*";
test[x][y]++;
return;
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (i == 1 && j == 1) star(x + n / 3 * i, y + n / 3 * j, n / 3, true);
else star(x + n / 3 * i, y + n / 3 * j, n / 3, blank);
}
}
}
}
blank는 공백 여부를 정해주는 변수, x, y는 점을 찍기 시작해나가는 위치를 나타내는 정수이다. n*n을 9개의 (n/3) * (n/3) 로 나누고, (아홉 번의 재귀함수 재참조) 그 중에 가운데일 때는 (i, j가 1일 때) blank를 true로 지정해줬다.
그리고 base condition에 다다랐을 때는 blank 변수에 따라 공백과 *을 2차원배열에 저장했다.
역시나 귀납적인 사고가 아주 중요한 문제였다. 별을 그냥 별로만 볼 것이 아니라, 하나의 "단위"로 봐야한다. n의 값에 따라 3*3, 9*9의 가운데가 공백인 형태가 들어갈 수 있다.
9. 백준 2448 - 별 찍기 - 11
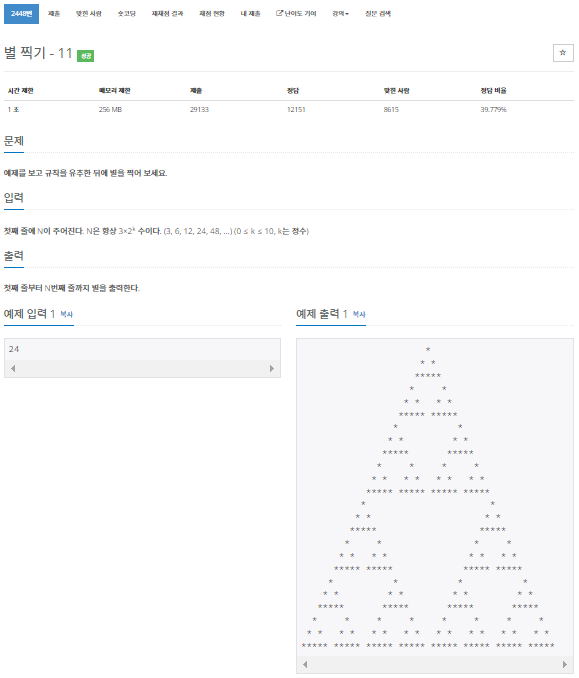
재귀적인 패턴에 대한 설명이 적기도 했고, 윗 문제보다 규칙을 파악하기 까다로운 문제였다. 먼저 6*3 크기의 작은 삼각형이 가장 작은 단위이고, (base condition) log(n/3) 번 만큼 패턴이 반복된다는 것을 발견했다. 그 밖에는 위의 문제와 비슷하게 해결했다.
package recursion;
import java.io.*;
import java.util.Arrays;
public class BOJ2448 {
static String[][] board;
static int[] dx = {0, 1, 1, 2, 2, 2, 2, 2};
static int[] dy = {0, -1, 1, -2, -1, 0, 1, 2};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
board = new String[n*2][n*2];
for (int i = 0; i < n*2; i++) {
Arrays.fill(board[i], " ");
}
triangleStar(0, n-1, n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < board[i].length; j++) {
bw.write(board[i][j]);
}
bw.newLine();
}
bw.close();
}
//시작 좌표는 x=0, y=23?
private static void triangleStar(int x, int y, int n) {
if (n==3) {
for (int i = 0; i < 8; i++) {
board[x+ dx[i]][y+ dy[i]] = "*";
}
return;
}
triangleStar(x, y, n/2);
triangleStar(x + n/2, y - n/2, n/2);
triangleStar(x + n/2, y + n/2, n/2);
}
}이전 문제는 정사각형을 행 열 모두 3등분하면 되었기 때문에 n/3 * i 를 더해주는 식으로 다음 단계의 좌표를 구할 수 있었는데, 이번 문제는 직접 그려보며 다음 단계의 좌표들을 파악했다. 전체 삼각형의 가장 위 꼭짓점을 시작으로 했을 때, 그 다음 꼭짓점의 행, 열 좌표 모두 n값의 절반만큼 변화했다. 그리고 base condition (n==3)에 다다랐을 때는, int배열로 만들어둔 규칙으로 board[][]에 그림을 그려줬다.
끝
사실 재귀 파트는 백날 설명을 듣는 것보다 계속 생각해보면서 문제를 풀고 감을 잡는 것이 더 좋은 방법인 것 같다. 자전거를 탈 줄 모르다가 언젠가부터 자연스럽게 체화되는 느낌이랑 비슷하다는 생각이 든다. 연습문제에서 적용한 핵심 세 가지에 항상 주의하며 계속해서 연습해보면, 재귀에 익숙해질 수 있을 것이라고 생각한다.
- 재귀의 핵심 : 귀납적 사고. base condition, 반복적으로 일어날 행위 를 바탕으로 함수 설계
- 귀납, 귀납, 귀납!!!
개념 및 연습문제 출처 : BaaaaaaarkingDog 블로그
