Clustering

242·2023년 6월 12일

패턴인식

목록 보기

9/9

K-Means

수식 부분만 정리해 두자...

$i$ : data point의 개수
$k$ : cluster의 개수, 즉 centroid의 개수

$k$ 개의 centroid를 랜덤하게 생성

$μ_1, μ_2, \cdots, μ_k ∈ \mathbb{R}^d$
( $k$ 개의 centroid는 given data space 내에 존재해야 함)
아래 과정을 수렴할 때까지 반복

for every $i$ , $c_i ≔ \argmin_j \begin{Vmatrix}x_i- μ_j\end{Vmatrix}^2$
각 점 $i$ 를 가까운 클러스터 $j$ 에 할당
(각 점과 centroid 간 거리를 가장 작게 하는 클러스터 $j$ 가 $c_i$ )

for every $j$ , $μ_j ≔ \displaystyle \frac {\sum^n_{i=1} 1\{c_i=j\}x_i}{\sum^n_{i=1}1\{c_i=j\}}$
각 클러스터에 할당된 점들을 이용해 중심값 $μ_j$ 를 업데이트

k-Means는 $k$ 의 값을 어떻게 할 것인지가 가장 중요함!
(주요 hyperparameter $k$ )

$k$ 를 효과적으로 select하기 위해 다음과 같은 방법을 이용한다.

특정 range 내에서 within-cluster variation을 가장 작게 하는 $k$ 를 고른다.

AWV = $\displaystyle \frac{\sum^k_{k=1}\sum_{x_i∈c_k}(x_i - μ_k)^2}k$

Hierarchical Clustering

계층적 군집화!

각각의 data point를 하나의 cluster로 취급
가장 가까운 cluster끼리 결합시켜 새로운 cluster를 만드는 과정을 반복, 결국 하나의 cluster만 남도록 함!

6개의 data point, 즉 6개 cluster에서 시작하는 naive example을 살펴보자.

cluster 수가 6개, 5개, ..., 1개가 되는 과정
매 반복 과정마다 거리를 계속 계산해야 하므로 expensive한 편

cluster 간의 '거리 계산'은 어떻게 이루어질까?

How to measure similarity(closeness)

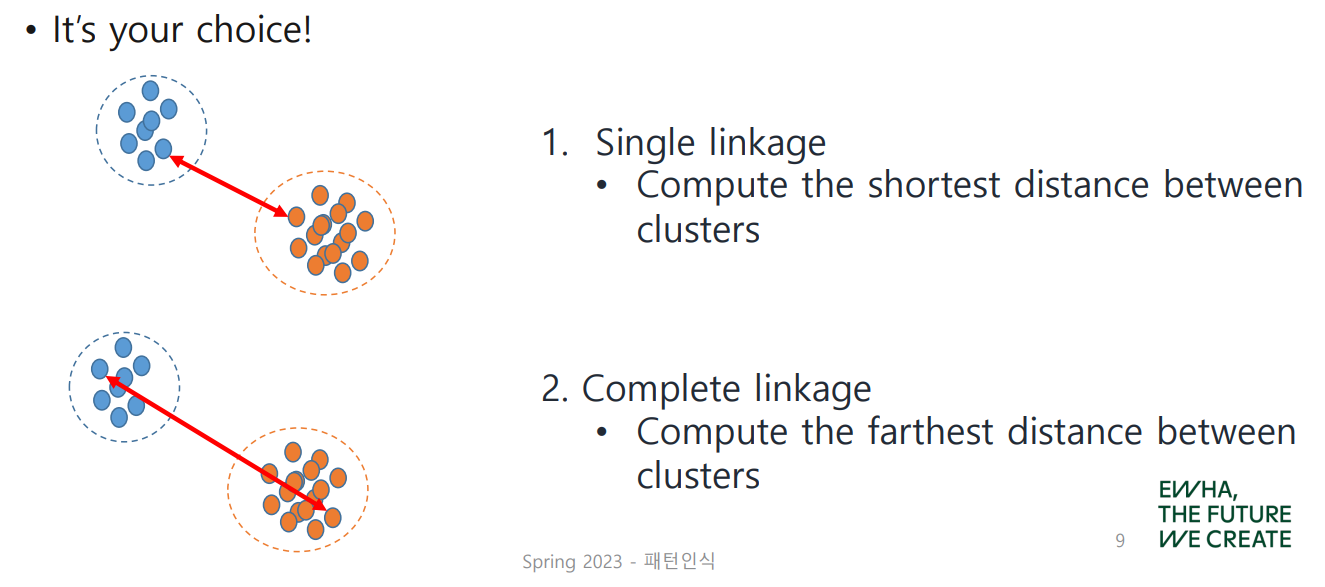
Single Linkage

cluster 간의 가장 짧은 거리를 계산하여 채택

Complete Linkage

cluster 간의 가장 먼 거리를 계산하여 채택

Average Linkage

cluster 내 모든 점끼리의 거리를 계산, 평균을 취하여 채택

Centroid Linkage

centroid 간의 거리를 계산하여 채택

How to choose clusters

개략적으로 얘기하자면 dendrogram을 그려 적당한 부분에서 자름으로써 cluster의 개수를 조절할 수 있음. (K-Means에 비해 이점을 갖는 부분)

모든 data point들 간의 거리(유사도)를 미리 구하고 첫 cluster를 만듦

거리일 경우 가장 짧은 것 선택
유사도일 경우 가장 높은 것 선택

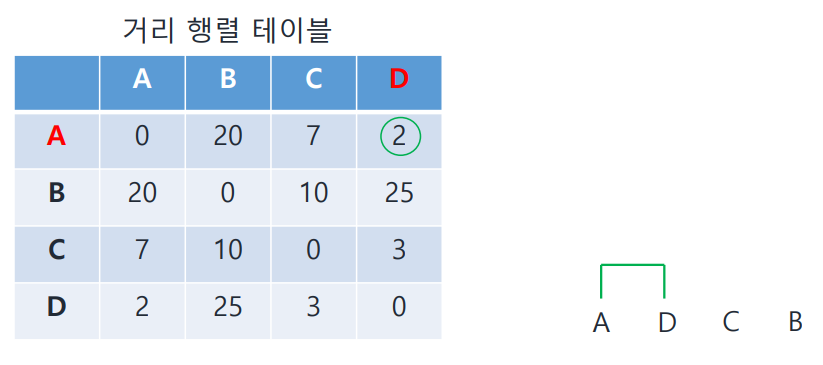
만들어진 cluster와 나머지 point 각각의 거리를 구하여 테이블 업데이트

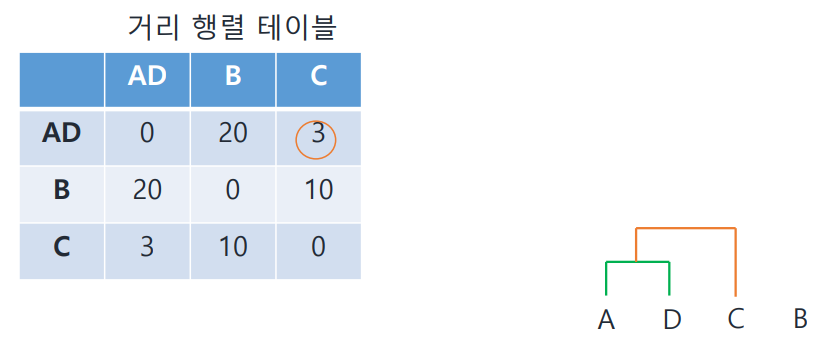
6개 data point에 대하여 적용한 모습은 아래와 같다.

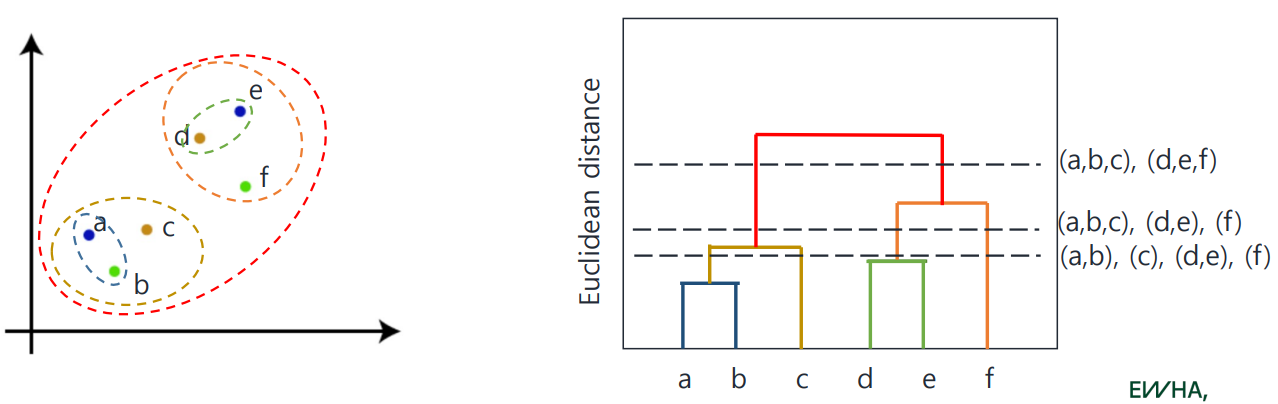
위처럼 적절히 잘라서 cluster의 개수를 원하는 대로 만들 수 있다.
이렇게 dendrogram을 이용한 방식은 장단점이 뚜렷함.

( $+$ ): cluster 개수 $k$ 를 미리, random하게 정할 필요 X
( $-$ ): cost가 비싸므로 큰 데이터에 적합하지 않음 (큰 리소스 필요)
pair-wise distance를 매번 구한다는 점이 효율성이 떨어짐

Gaussian Mixture Model

GMM이 이거구나
아니 수업 들어놓고 기억을 못해서 누가 GMM 얘기할 때마다 매번 GBM을 잘못 말한 건가? 이러고 있었따

꺄악 이거 어렵다
대충 나만 알아보게 쓰겠습니다

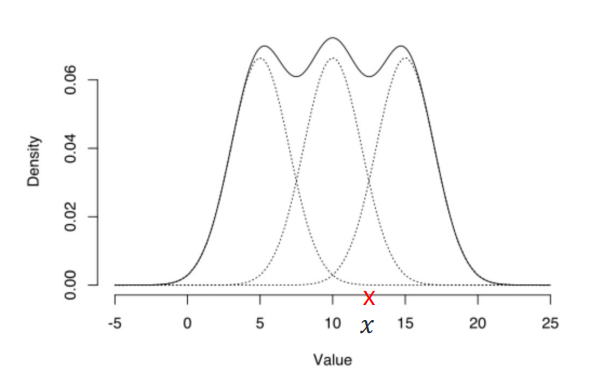
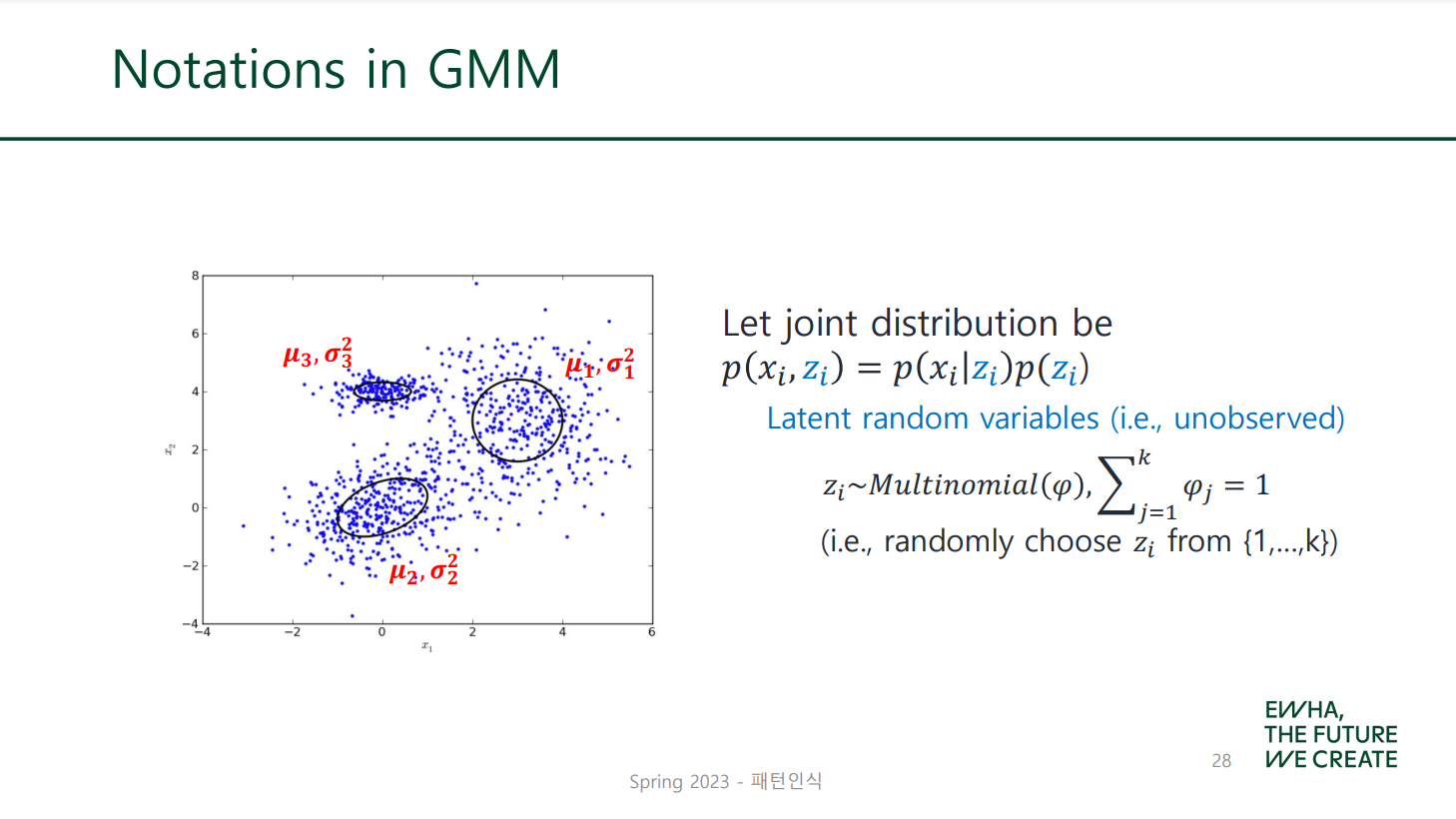
GMM은 distribution-based clustering으로, 각 분포가 하나의 cluster라고 생각하면 됨!

위 그림과 같이 여러 개의 가우시안 분포가 혼합된 형태를 Gaussian Mixture Model(GMM) 혹은 가우시안 혼합모델이라고 함.

3개의 가우시안 분포가 혼합된 이 모델에서, 주어진 데이터에 대한 density를 아래와 같이 구할 수 있음 (데이터가 이 모델에 속할 확률 계산)

$p(x) = \displaystyle \sum^3_{k=1} \pi_k N(x | μ_k, Σ_k)$

여기서 $\pi_k$ 는 혼합계수로, 이것의 비율만큼 각 분포가 $x$ 에 영향을 준다고 볼 수 있다. 각 분포에 대한 혼합계수는 모두 $0$ 에서 $1$ 사이의 값이며, 전부 합하면 $1$ 이 된다!

혼합계수 $\pi_k$ 에 대한 식은 다음과 같다.

$\pi_k = p(z=k)$ : 즉, $z$ 가 $k$ 일 확률

$z$ 는 latent variable(잠재변수)로, 관찰로 측정할 수 없으며 필요에 의해 정의할 때만 사용하는 숨겨진 변수이다.
말 어려운데 결국 그냥 주어진 데이터가 여러 개 가우시안 분포 중 $k$ 번째 것을 따를 확률을 말하는 것임

다시 구체적으로 풀어 쓰면 다음과 같음

$\pi_k = p(z=k;μ_k, Σ_k)$
혼합계수란 $x$ 가 $k$ 번째 클러스터에 속할 확률이자,
즉 평균이 $μ_k$ 이고 분산이 $Σ_k$ 인 가우시안 분포를 따를 확률

혼합모델을 클러스터링에 활용하는 방법을 정리하자면 다음과 같다.

각 가우시안 분포에 데이터가 속할 확률(density)을 계산하여, 높은 확률 가진 분포(클러스터)에 할당
각 가우시안 분포의 평균과 분산을 MLE를 사용해 계속적으로 추정, 업데이트하는 과정을 반복하여 최대 likelihood를 얻는 모델을 구함

label이 없는 데이터에 대해 분포를 예측하고(Expectation)
log likelihood를 계산하여 이를 최대화하는 방향으로 나아감(Maximization)
이러한 알고리즘을 EM Algorithm이라고 부른다!

EM Algorithm

동전 던지기 예제를 통해 알아보자.
2개의 동전 A, B가 있을 때 랜덤하게 하나를 골라 10번 던지고 그 결과를 다음과 같이 적는다. (총 5번 시행)

EM 알고리즘을 적용하기 위해 각 시행마다 어떤 동전을 뽑았는지 모르는 상황에서 시작한다. 각 차수에 어떤 동전을 사용했는지 확률을 계산해가며 예측하는 것이 우리의 목표이고, 식으로 나타내면 다음과 같다.

n차 시행에서...

동전 A를 사용했을 확률 $\pi_A = p(z=A)$

동전 B를 사용했을 확률 $\pi_B = p(z=B)$

E-step

우선 1차 시행에 대해 계산해보자!

동전 A의 앞면이 나올 확률을 $\theta_A$ , B의 앞면이 나올 확률을 $\theta_B$ 라고 하자. 이에 대한 초깃값은 랜덤하게 결정한다.

$\theta_A^0 = 0.6, \theta_B^0 = 0.5$ (초깃값이므로 $0$ 붙였으며 계속 업데이트할 것)
이에 따라 각 동전의 뒷면에 대한 확률은 각각 $0.4$ , $0.5$ 가 될 것이며, 이 값은 1~5차 시행 모두에서 이용된다.

1차 시행의 결과는 앞 뒤 뒤 뒤 앞 앞 뒤 앞 뒤 앞으로 앞뒤가 각각 5번이다. 위 확률을 적용해보자.

1차 시행에서...

동전 A를 사용했을 경우 $0.6^50.4^5 = 7.96e^{-5}$

동전 B를 사용했을 경우 $0.5^50.5^5 = 9.76e^{-5}$

이에 따라 1차 시행에서 각 동전을 사용했을 확률을 구할 수 있다.

1차 시행에서...

동전 A를 사용했을 확률 $\pi_A = 7.96e^{-5} / (7.96e^{-5} + 9.76e^{-5}) = 0.45$

동전 B를 사용했을 확률 $\pi_B = 9.76e^{-5} / (7.96e^{-5} + 9.76e^{-5}) = 0.55$

1차 시행에서는 동전 B를 사용했을 확률이 $0.55$ 로 더 높다!
두 확률을 더하면 $1$ 이 된다는 점도 확인할 수 있다.

이렇게 $\pi_A$ 와 $\pi_B$ 를 구하는 과정을 1~5차 시행에 대해 반복하는 것으로 E-step은 마무리가 된다. 모든 시행에 대해 계산해보기!!!!!

M-step

이번에는 초깃값으로 설정했던 $\theta_A^0$ , $\theta_B^0$ 를 업데이트하는 과정이라고 볼 수 있다. E-step에서 구한 $\pi_A$ 와 $\pi_B$ 를 이용하게 된다.

1차 시행의 결과 앞5, 뒤5인 것을 확인했으므로
각 동전을 사용했을 확률에 이 값을 곱해 다음과 같은 값을 얻는다.

1차 시행에서...

동전 A의 경우 앞은 $0.45 \times 5$ , 뒤는 $0.45 \times 5$

동전 B의 경우 앞은 $0.55 \times 5$ , 뒤는 $0.55 \times 5$

위 E-step에서는 1차 시행에 대한 결과만 얻었지만, 2~5차 시행에서도 같은 과정을 거쳐 각 동전에 대한 확률을 구했다고 가정하고 다음과 같이 표를 채웠다.

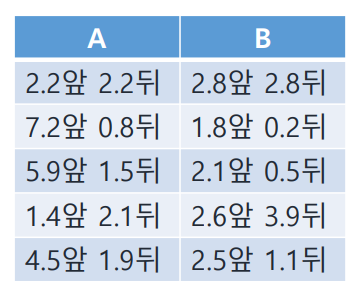
$\theta_A^0$ , $\theta_B^0$ 에 대한 업데이트는 이 표를 이용하여 진행된다. 우선 모든 앞뒤에 대한 확률값을 더한 뒤 그 값을 이용한다.

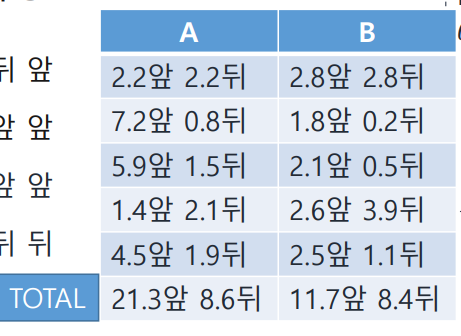
업데이트에 대한 식은 다음과 같다.

$\theta_A^1 = \displaystyle \frac {21.3}{21.3+8.6} \approx 0.71$

$\theta_B^1 = \displaystyle \frac {11.7}{11.7+8.4} \approx 0.58$

이 값을 이용하여 같은 과정을 반복한다...

아래 페이지들은 뭔지 모르겟군.

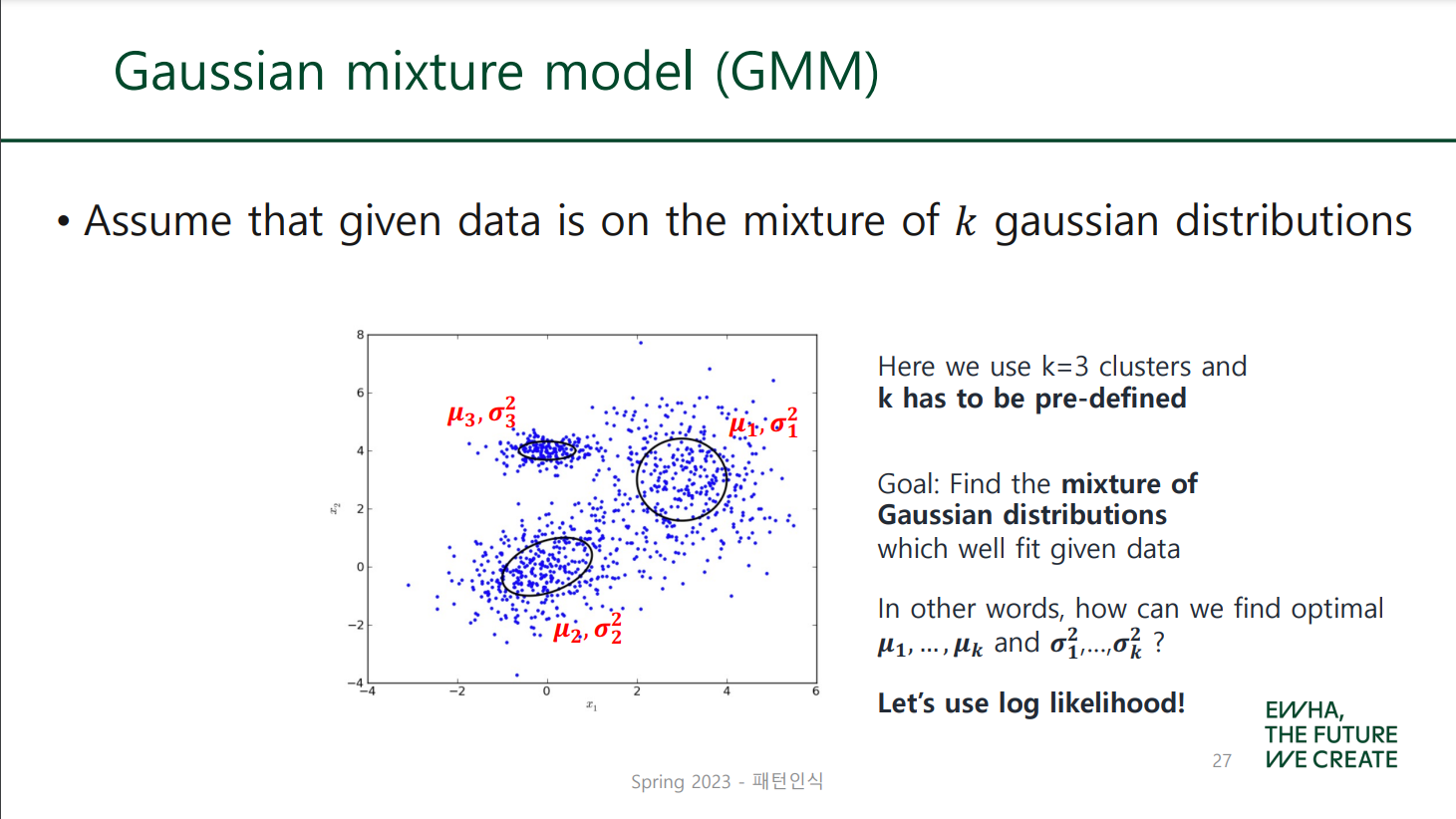
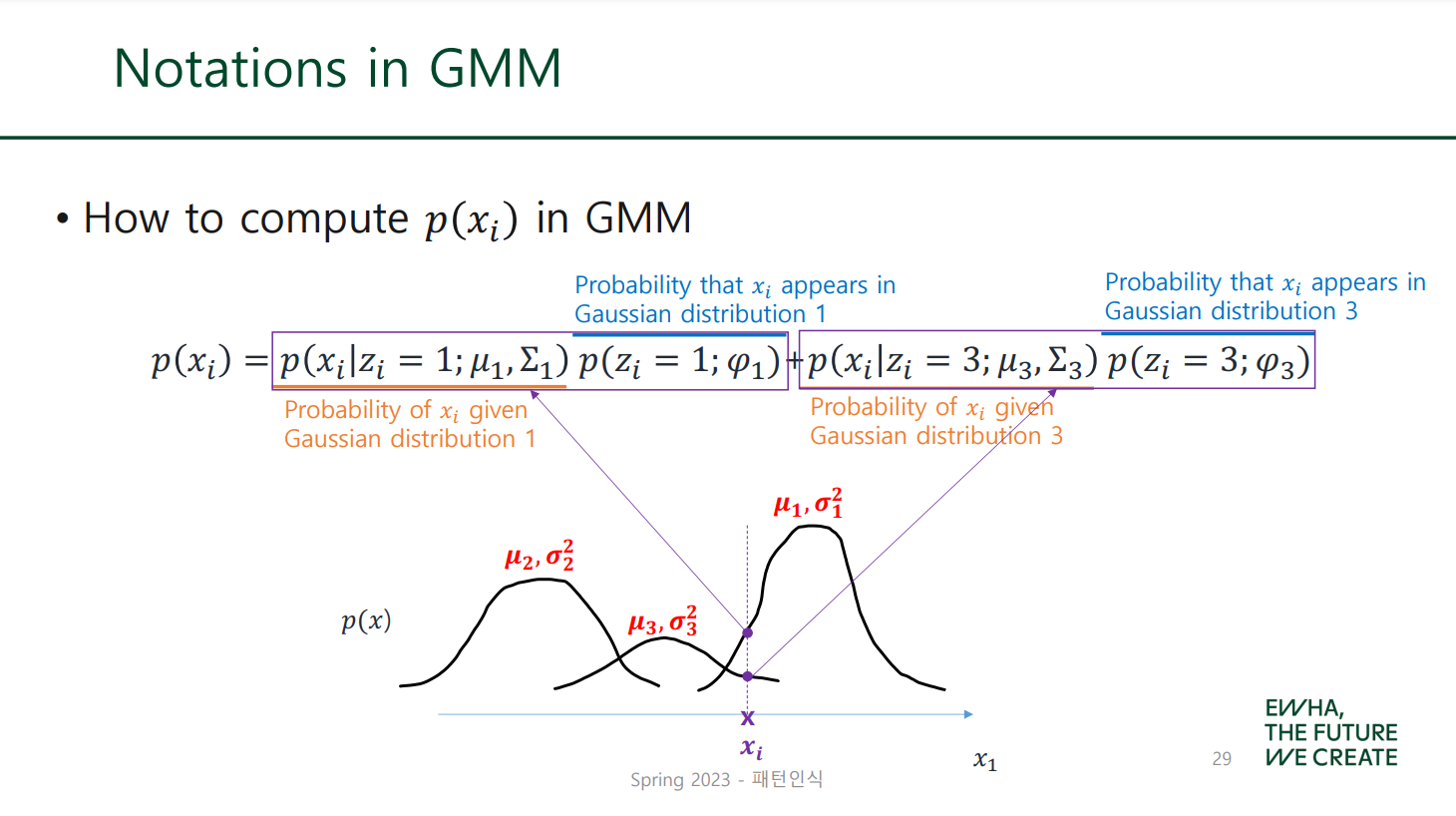
$p(x_i) = p(x_i | z_i=1;μ_1, Σ_1)p(z_i=1;φ_1) + p(x_i|z_i=3;μ_3, Σ_3)p(z_i=3;φ_3)$

$p(x_i | z_i=1;μ_1, Σ_1)$ : 주어진 데이터 점 $x_i$ 가 가우시안 분포 1을 따를 확률 (likelihood, 혹은 density)
$p(z_i=1;φ_1)$ : 혼합계수, probability that $x_i$ appears in GD 1
이걸 어케 번역해야 하냐.... 대강 bayes rule에서의 prior 역할을 한다!
혼합계수이니 각 분포가 데이터에 미치는 영향을 나타냄

일반화한 식은 다음과 같다.

$p(x_i) = \displaystyle \sum_{j=1}^k p(x_i | z_i=j;μ_j, Σ_j)p(z_i=j;φ_j)$
$i$ 번째 data point가 $j$ 번째 가우시안 분포를 따를 확률

참고자료

242

이전 포스트