k-Nearest Neighbors

242·2023년 5월 20일

패턴인식

목록 보기

8/9

k-Nearest Neighbors (k-NN)

supervised learning의 일종(label 주어짐)인 거리 기반 분류 모델

🍜 거리 기반 분류 모델

testing data의 이웃들의 label을 고려하여 분류
- 이웃을 결정하기 위한 거리 측정 (이용할 metrics 결정)
- 고려할 이웃의 수 ( $k$ 값) 결정

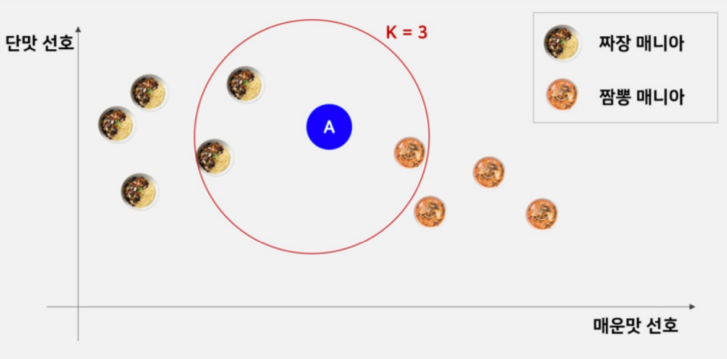
(출처: $k=3$ , 즉 홀수 개의 이웃을 고려하는 예시)

💥 동점 상황 발생

위와 같은 이진 분류에서 $k$ 의 값을 짝수로 설정하면 동점인 경우가 발생할 수 있으므로 $k$ 값으로는 홀수를 사용하는 것이 정석이다. 동점 상황이 발생하면 그냥 random한 label로 분류된다.

k-NN의 특징

fitting(모델 학습시키기)이 필요하지 않음
- parameter optimizing 등의 과정 X
- 학습데이터 포인트만 기억하고 있으면 됨
- memory-based / instance-based / lazy learning
classifier는 테스트 데이터와 가장 가까운 k개의 학습 데이터를 검색하고, 이들의 most common label을 테스트 데이터에 할당
cheap training but expensive testing

사실상 맨 위 내용이랑 합쳐도 되는 부분인데 ㅋ ㅋ
PPT 순서대로 갑시다....

k-NN Metrics

testing data point $z$ 가 주어졌을 때, 이와 가장 가까운 $k$ 개의 training point를 찾은 뒤 이 $k$ 개의 이웃들로부터 majority vote(출현 빈도)를 계산하여 label을 부여한다.

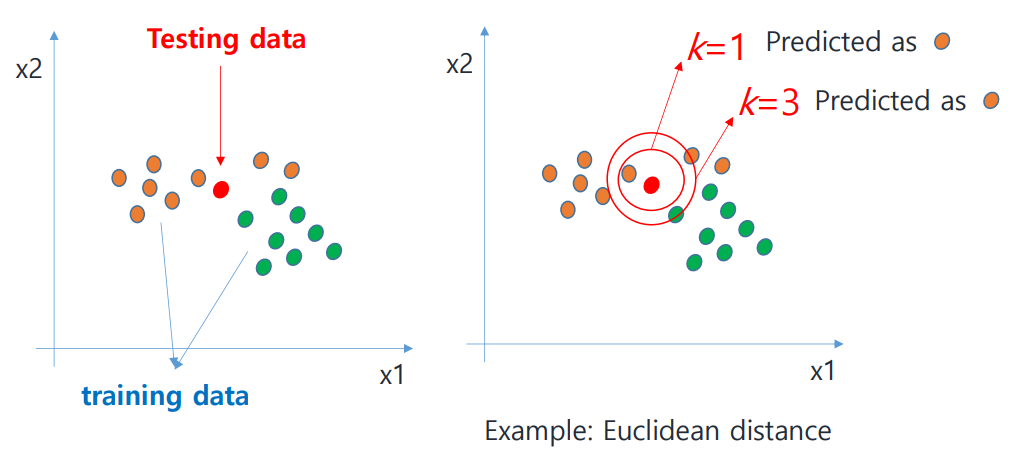
'가깝다'는 것은 어떻게 측정할 수 있을까?

🎄 Distance-based Metrics

Euclidean distance
Manhattan distance
Minkowski distance

🎄 Similarity-based Metrics

Cosine similarity
Jaccard similarity

🎄 Others

Hamming distance

위와 같이, 거리/유사도(distance or similarity)로 계산하게 된다.
거리 기반 metircs부터 살펴보자.

Distance-based Metrics

Euclidean Distance

L2 distance, L2-norm
가장 널리 쓰이는 방식이다.

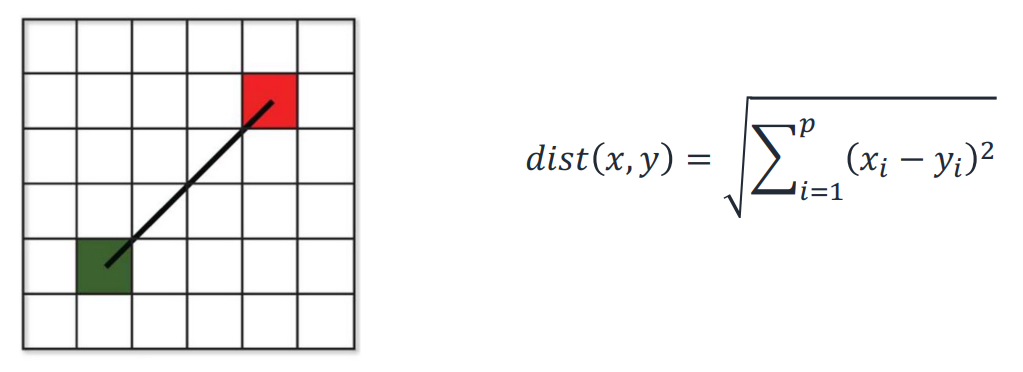
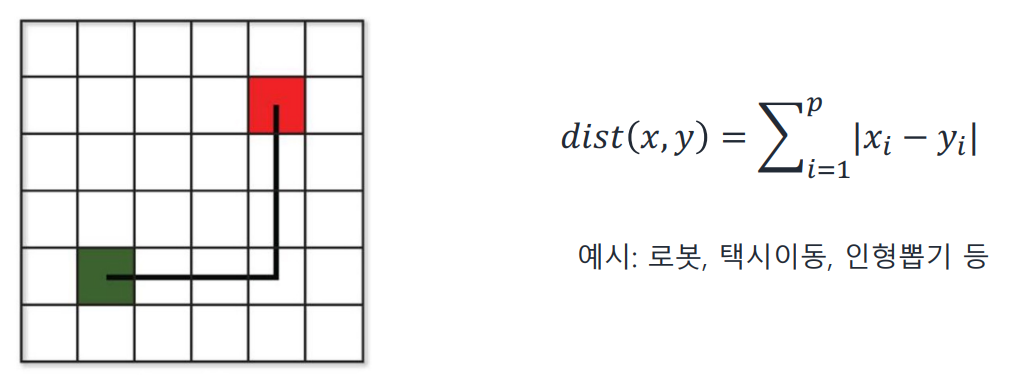
$dist(x, y) = \displaystyle \sqrt{\sum^p_{i=1} (x_i - y_i)^2}$

Manhattan Distance

L1 distance, L1-norm
차이의 절댓값의 합! L2를 쓸 수 없는 상황에 주로 쓰게 된다.
ex) 로봇, 택시이동, 인형뽑기 등

$dist(x, y) = \displaystyle \sum^p_{i=1}|x_i - y_i|$

Chevyshev Distance

L∞ distance, L∞-norm
각 dimension의 L1 거리 중 최댓값이다!

$dist(x, y) = max_i(x_i - y_i)$

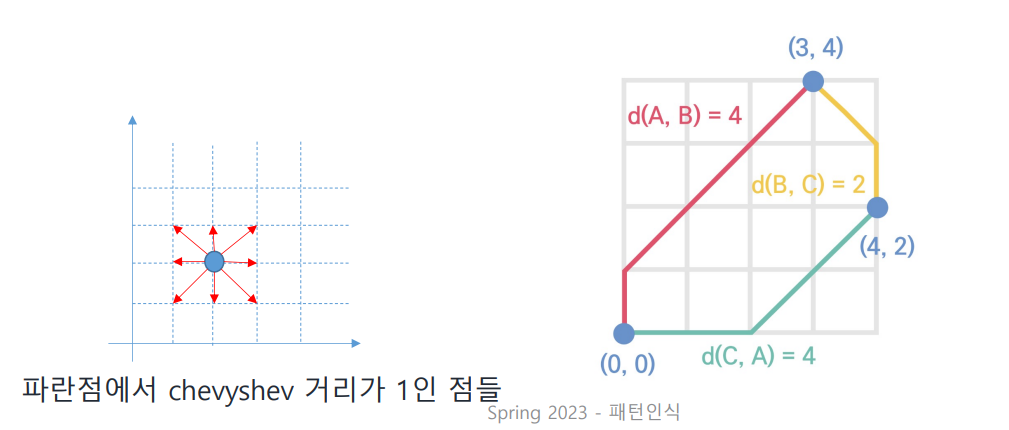
예를 들어 (0, 0)에서 (4, 2)까지의 chevyshev 거리는 4이다.

Minkowski Distance

Lp distance, Lp-norm
Euclidean과 Manhattan distance의 generalized form이다.

$dist(x,y) = \displaystyle (\sum^n_{i=1} (x_i - y_i)^p)^{\frac 1p}$

$p=1$ : 맨해튼 거리

$p=2$ : 유클리디안 거리

$p = \infin$ : 체비셰프 거리

유사도 기반 metrics를 알아보자.

Similarity-based Metrics

Cosine Similarity

두 벡터 간의 코사인 각도를 계산하여 유사도를 결정하며, 같은 방향을 가리킬수록 유사도는 높아진다. ( $-1$ ~ $1$ 사이 값)

$sim(x, y) = \cos(\theta) = \displaystyle \frac {\sum^p_{i=1}x_i \times y_i}{\sqrt{\sum^p_{i=1}x^2_i}\sqrt{\sum^p_{i=1}y^2_i}}$

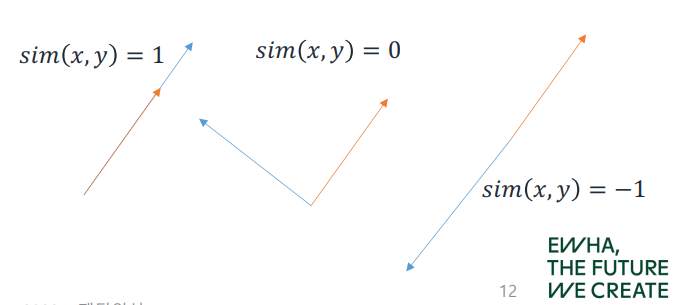
Jaccard Similarity

주로 NLP에서 사용된다. (e.g. 문서 유사도 비교)

$sim(x, y) = \displaystyle \frac {|x∩y|}{|x∪y|}$

e.g.

다음과 같은 두 문장이 있다고 하자.

AI is our friend and it has been friendly.
AI and humans have always been friendly.

중복을 제외한 전체 단어 중 겹치는 것의 개수가 자카드 유사도이므로, $5/10$ 이라는 값을 얻게 된다.

마지막으로 그 외에 속하는 hamming distance가 있다.

Hamming Distance

주로 NLP에서 사용되며, (e.g. 문서 유사도 비교) 같은 길이를 가진 두 이진수를 비교할 때도 사용할 수 있다.

두 문자열 중 하나의 문자열에 대해 몇 개의 문자를 바꿔야 문자열이 서로 같아지는지, 즉 두 문자열에서 서로 다른 문자의 개수를 나타내는 개념이라고 볼 수 있다.

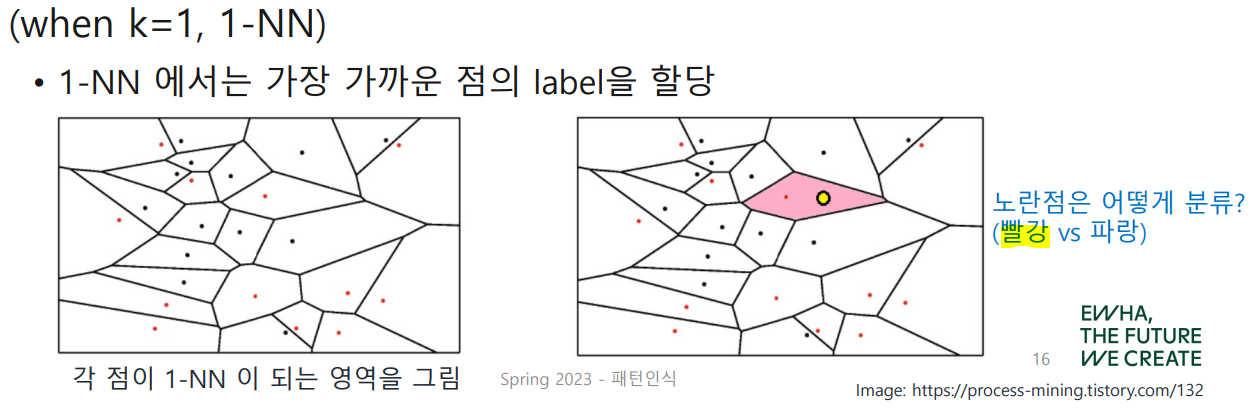
Decision Boundary in k-NN

k-NN에서 직접적으로 decision boundary를 계산해주지는 않지만, 다음과 같이 voronoi tessellation을 그려 추론해볼 수 있다.

k-NN Algorithm

k-NN 알고리즘의 작동 과정을 살펴보자.

Standardize, 즉 정규화를 반드시 해야 한다! (to have $μ=0$ and $σ^2=1$ )
ex) 만약 특정 feature의 수치는 1~10, 다른 feature의 수치는 1~100,000,000로 표현될 경우 정규화를 하지 않으면 범위가 큰 feature가 거리에 더 큰 영향을 주게 된다.
testing sample을 입력, 가장 가까운 $k$ 개의 train sample을 찾는다.
가장 많이 나온 class로 분류한다.

$\hat y = \argmax_{y_z}\sum^k_{i=1}I(y_z=y_i)$

Indicator function! 같으면 $1$ , 다르면 $0$

$y_z$ : testing data $x_z$ 의 label

$y_i$ : $k$ 개의 가장 가까운 이웃의 label

How k impacts the decision boundary?

label이 $0$ 또는 $1$ 인 Binary Classification 상황을 가정해 보자.
( $\hat y(x) =\frac 1k \sum^{N_k}_{i=1} y_i$ 이며, 여기서는 $0.5$ 로 가정)
$\hat y(x) = 0.5$ 라는 게 무슨 뜻이지

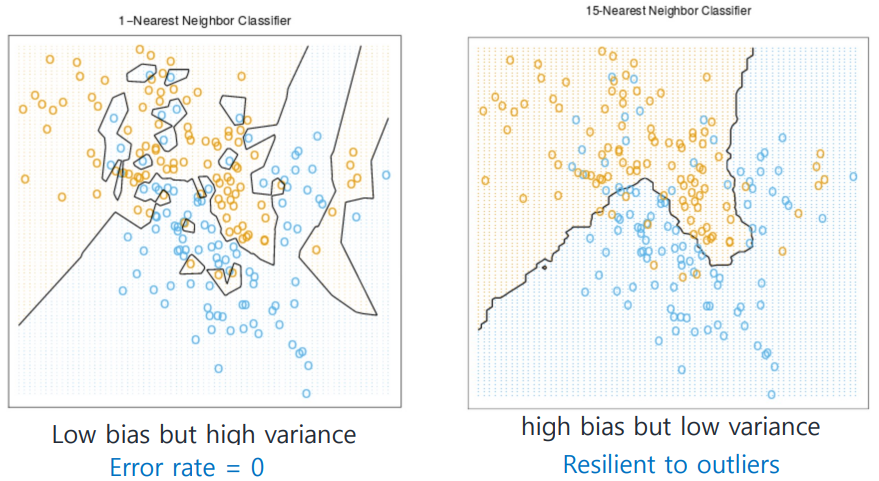
$k=1$ : error rate는 $0$ 이지만, outlier 배제를 전혀 못하고 있다.
$k=15$ : resilient to outliers, 즉 outlier에 굴하지 않는다...

$k$ 가 줄어들수록 물론 오판율은 매우 떨어지지만, accuracy가 증가한다고 무조건 좋은 모델로 평가할 수는 없다.

$k$ 의 값에 따라 어떤 변화가 있을까?

How k treats the noise point?

$k$ 를 증가시킬수록...

noise sample에 덜 민감해진다.
outlier를 handling하기 좋아진다.

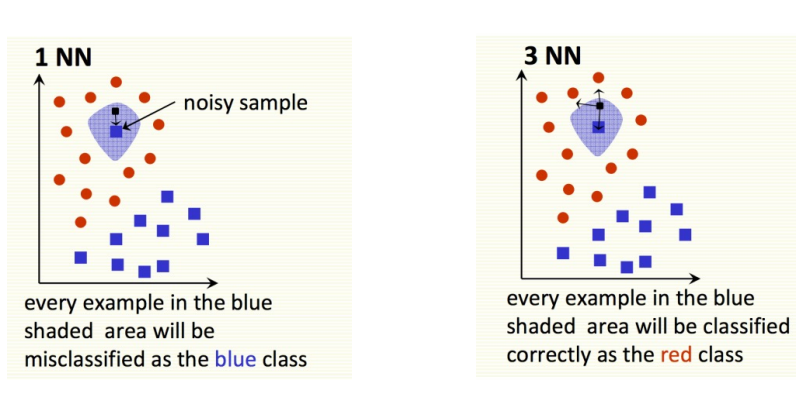
위 그림에서는 표시된 파란 점을 noise로 판단할 수 있다. 만약 $k=1$ 인 경우 noise sample 근처에 testing sample이 떨어지면 blue로 잘못 분류되지만, $k$ 를 증가시킬수록 red로 맞게 분류될 가능성이 커진다.

이러한 점을 고려하여 적절한 $k$ 값을 찾는 것이 중요하다.

How to choose k

일반적으로 $k$ 가 클수록 testing performance가 높아지는 경향을 보인다.
하지만 $k$ 가 너무 크다면, 이웃이 아닌 sample까지 이웃으로 판단할 가능성이 커지므로 무조건 큰 $k$ 가 좋은 것은 아니다. (당연~)

보통 Cross Validation을 사용해 최적의 $k$ 를 찾으며, 추천되는 크기는 $k<\sqrt n$ 이다. ( $n$ : training sample의 전체 개수)

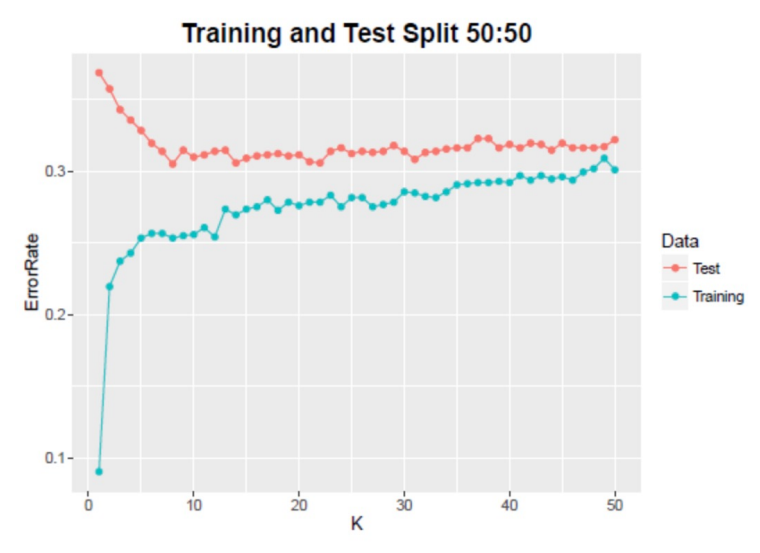
$k$ 값에 따른 training set과 testing set의 error를 나타낸 그래프이다. $k$ 값이 증가할수록 testing set에 대한 error가 감소하고 있음을 확인할 수 있다.

k를 낮출수록...

testing 시간이 길어진다. (expensive)
1-NN을 찾기 위해서는 모든 training sample에 대한 거리를 계산해야 한다.
높은 용량을 필요로 한다.
모든 training sample을 저장해야 하기 때문!

참고자료

242

이전 포스트

Model Assessment

다음 포스트