Linear Models for Regressions (1)

242·2023년 3월 12일

목록 보기

1/9

Model Representation

3월에 여는 편의점의 수익을 예측하는 상황을 가정해 보자.

Month	# visited customers	Revenue
Aug	6000	$60K
Jul	5200	$52K
Jun	4500	$50K
...	...	...

원하는 정답(label)이 존재할 경우 Supervised Learning을 이용한다.
이 경우 label은 수익!

🐱‍🏍 Linear Regression

Supervised Learning의 일종으로, 주어진 데이터를 나타내는 최적의 직선을 찾아냄으로써 input(x)와 output(y) 사이의 관계를 도출해내는 과정!

✔ Univariate Linear Regression

Univariate: x column이 하나인 경우

Month	# visited customers (x)	Revenue (y)
Aug	6000	$60K
Jul	5200	$52K
Jun	4500	$50K
...	...	...

이 경우는 Univariate Linear Regression이다.

Terminologies (용어)

m: # training examples

x: input variables or features

y: output variables or "target" variable

(x,y): one training example

( $x^i$ , $y^i$ ): i -th training example

주어진 표대로, customers에 따른 revenue를 좌표평면에 표시해 보자.

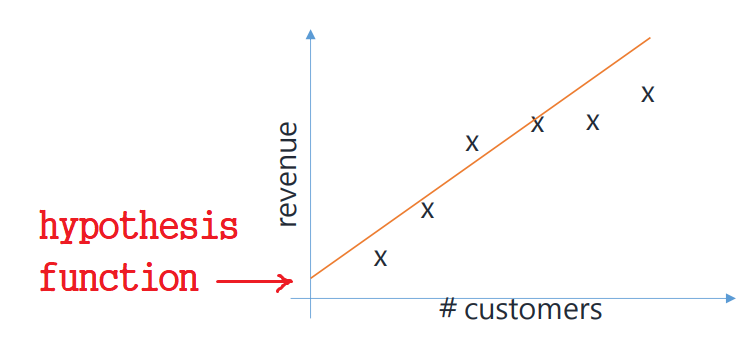
✔ Hypothesis Function

input(x)와 output(y) 사이의 관계를 정의하는 함수이다.
앞에서 언급한 주어진 데이터를 나타내는 최적의 직선을 표현하기 위해 사용하는 식!

Hypothesis Function in Univariate Linear Regression

Hypothesis Function Form (Univariate)

$f(X) = β_0 + β_1X_1$

$β_0$ 는 bias값으로, 유무는 그닥 상관없다.
가장 적절한 $β_0$ 와 $β_1$ 값을 찾는 것이, 즉 이 값을 조정하여 better fitting line을 찾는 것이 곧 Linear Reression의 과정이다!

이때 사용할 수 있는 것이...

✔ Cost Function (Error Function)

f(X)와 y 사이의 gap을 측정하는 Error Function

Cost Function in Univariate Linear Regression

Cost Function Form (Univariate)

$\displaystyle\sum_{i=1}^{N}\{y_i - f(x_i)\}(\frac1N)$

$y_i - f(x_i)$ 을 제곱해도 되고, 안 해도 된다.
$\frac1N$ 또한 빠져도 되며, 심지어는 $\frac1{2N}$ 으로 들어가도 상관없다. 우리는 β값을 찾는 것이니 상수곱이 있든 없든 상관이 없다는 것이다. 뭐라는지 모르겟다 계산해봐야 알겟다 ㅁㅊ

cost function은 형태가 다양한가 보다. 그래도 제곱+ $\frac1{2N}$ 들어간 걸 제일 많이 쓰지만... 후에 나올 LSE랑 형태가 겹쳐서 그런가? 왜 여기선 이렇게 되어 있는지 영 모르겠지만 암튼 교수님은 이렇게 소개하셨다.

ex) If we use $β_1$ =10, $β_0$ =0

X	y	f(X)	Error(y-f(X))
6000	$60K	60K	0
5200	$52K	52K	0
4500	$50K	45K	5K

Univariate만 다뤄도 된다면 참 좋겠지만,
우리는 벡터의 노예... Multivariate 등장이다.

✔ Multivariate Linear Regression

Multivariate: x column, 즉 feature가 여러 개인 경우

Month	# visited customers	Spending per Customer	Revenue
Aug	6000	$13	$60K
Jul	5200	$15	$52K
Jun	4500	$12	$50K
...	...	...	...

이 경우는 Multivariate Linear Regression이다.

Hypothesis Function in Multivariate Linear Regression

Hypothesis Function Form (Multivariate)

$f(X) = β_0 + \displaystyle\sum_{j=1}^{m}(X_jβ_j)$

Terminologies (용어)

$β_0$ : Bias (as we usually put $X_0$ =1)

$β_j$ : Unknown parameters

$X_j$ : Input variables

f(X): model(predictor) or hypothesis

m: number of features

Y: Target variables

앞의 편의점(Multivariate) 예시에 대입하여 생각해 보자. (m=2) 이 경우...
$f(X) = β_0 + \displaystyle\sum_{j=1}^{2}(X_jβ_j)$

$X_1$ : Number of customers
$X_2$ : Spending per customer
$X^{Jul}_1$ (or $X_{1Jul}$ ): Number of customers in Jul
$X^{Jul}_2$ (or $X_{2Jul}$ ): per-customer spending in Jul
$Y$ : Sales
$Y^{Jul}$ (or $Y_{Jul}$ ): Revenue in Jul

가장 적절한 $β_j$ 값을 찾아냄으로써 최적의 직선을 찾을 수 있겠다!
어떻게 찾느냐!? 역시 Cost Function 활용이다.

나 필기 보니까 $X^{Jul}_1$ , $X^{Jul}_2$ 에만 표시해 놨던데 이유 안 써 놔서 왜인지 모르겠다 녹강 확인하기

Cost Function in Multivariate Linear Regression

PPT에는 Least (Mean) Squares라고 되어 있는데...
참고: https://stats.stackexchange.com/questions/146092/mean-squared-error-versus-least-squared-error-which-one-to-compare-datasets

위 답변 내용에 따르면 minimizing the "total" euclidean distance between a line and the data points, 즉 선형 회귀 모델을 생성할 때 쓰이는 것이 Least Square Error (LSE) 이다.

Mean Square Error (MSE) 는 이렇게 생성된 모델을 평가할 때 쓰는 것이지만, LSE와 수식이 똑같다. 어떻게 이럴 수가

암튼 LSE에 대하여 알아보자.
끝을 method로 해서 LSM라고 쓰기도 하나 봐.

Least Squares

Cost Function in Multivariate Linear Regression이 곧 LSE(LSM)이다. N개의 training observations( $(x_1, y_1)$ , ... , $(x_N, y_N)$ , 즉 학습데이터)가 parameter 추정에 이용된다.

$J(β) = \displaystyle\sum_{i=1}^{N}\{y_i - f(x_i)\}^2 = \displaystyle\sum_{i=1}^{N}\{y_i - (β_0 + \displaystyle\sum_{j=1}^{p}X_{ij}β_j)\}^2$

슬프게도 $x_i$ 는 scalar가 아냐...

$x_i = \begin{bmatrix}x_{i1} \\ x_{i2} \\ ... \\ x_{ip} \end{bmatrix}$
$f(x_i)$ : Cost (Error) Function
$p$ : # features

그리고 $y_i - f(x_i)$ 값을 Residual이라고 하나 보다.
앞서 말했듯 $\displaystyle\frac1{2N}$ 같은 거 들어가도 된다. 다만 교수님은 위처럼 쓰셧음.

Fit the least squares $ℝ^{p+1}$ ― dimensional space 라고 돼 있는데
이거 뭔 뜻이지 못 알아먹겠음

p는 지금 feature 개수잖아?
unknown parameter $β$ 가 $β_0$ , $β_1$ , ..., $β_p$ 까지 p+1개 나올 수 있다는 말인 듯
$β = \begin{bmatrix}β_0 \\ β_1 \\ ... \\ β_p \end{bmatrix}$ 이러면 p+1차원이니까

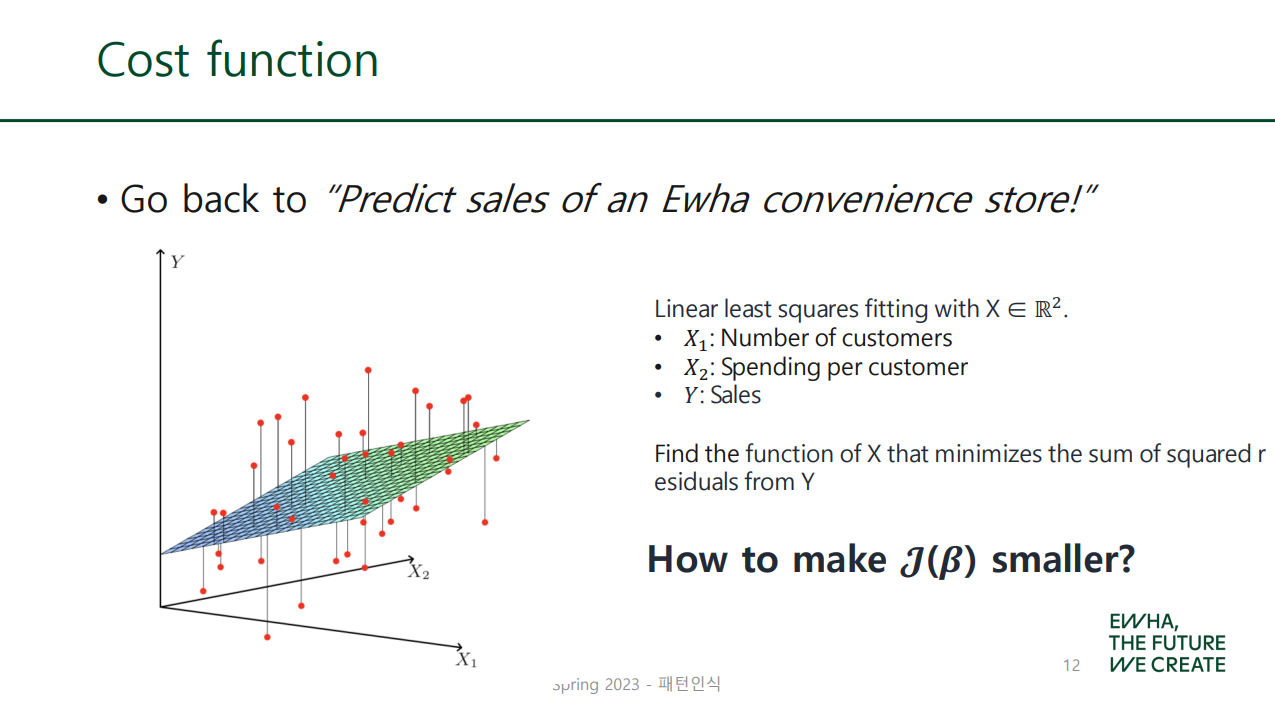
대충 위 cost function을 그래프로 그려 보면 이렇더라~

🐱‍🚀 잠깐 정리!

여태 한 얘기를 간단히 종합하자면,

input data(x)로 hypothesis function을 만들어, 이 값이 output data(y)와 가까워지도록 하는 것이 linear regression의 목표!
f(x)를 정의하기 위해서는 parameter(β)값을 정해야 하며, 이에 사용되는 것이 cost function!
간략히 보면 y-f(x)값이 곧 error, 즉 cost function이며 이를 최소로 만들어야 좋은 모델... 최소가 되게 만드는 β를 어떻게 구할 것인가!?

그 방법이 바로...

🐱‍🏍 Gradient Descent Algorithm

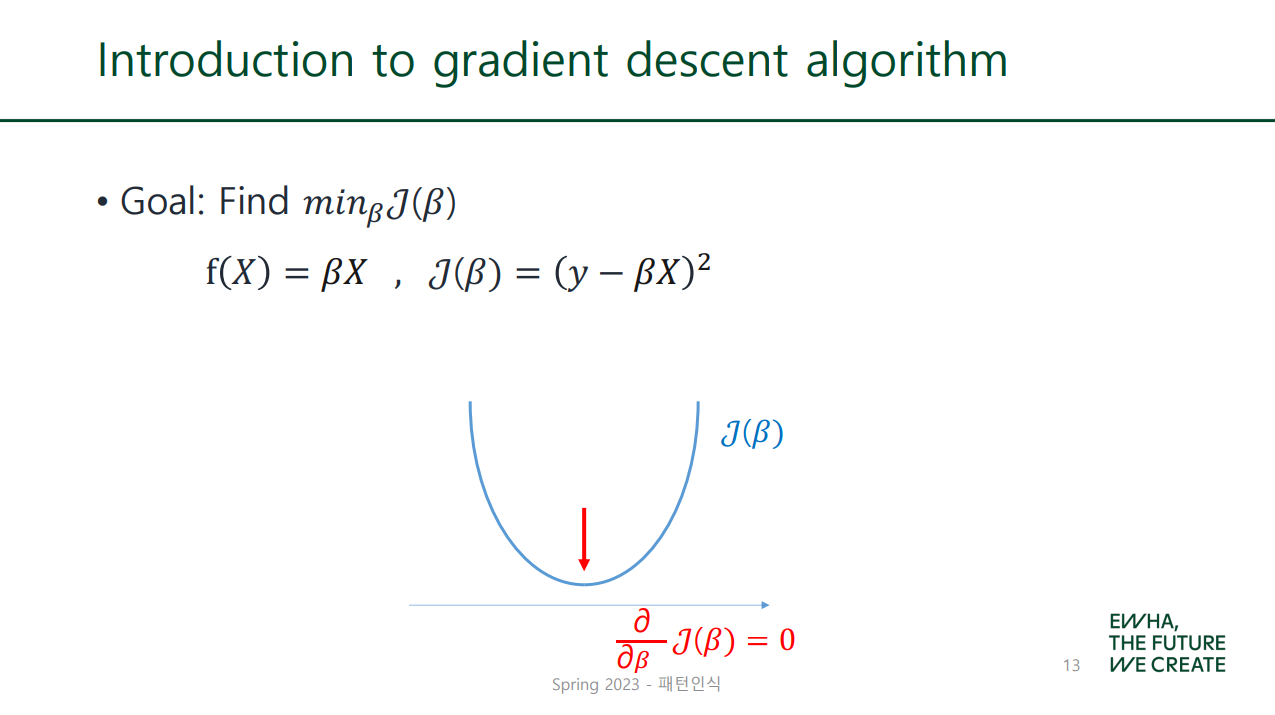
우리 미분 배웟잖아!
미분값이 0이 되는 지점을 계산으로 구하면 최솟값이 나오리라- 결국 이게 gradient descent algorithm이었던 게다.

Gradient Descent Algorithm with Linear Model

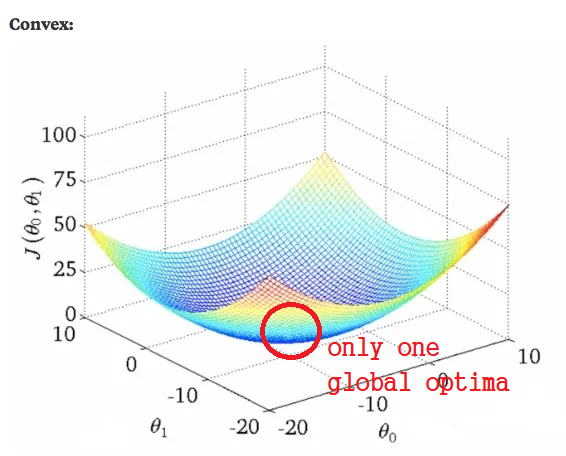
Gradient Descent Algorithm with Non-linear Model

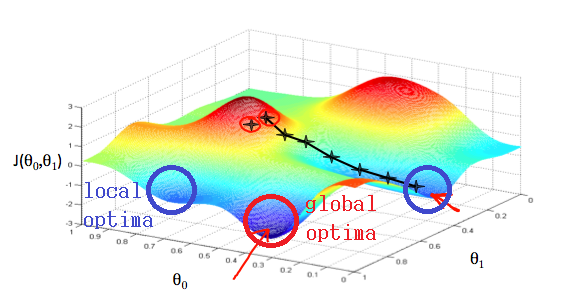
🐱‍👓 Linear vs. Non-linear

	feature 개수	optima의 개수
1개	2차원	Linear
여러 개	n차원	Non-linear

n>2

Derivation

Initialize $β$
Repeatedly updates $β_j$ as follows.

$β_j ← β_j - α\displaystyle\fracδ{δβ_j}J(β)$

$β_j$ 는 feature 수에 따라 그 개수가 늘어난다.
$α$ 는 Learning Rate로 update 속도를 조절한다. (size of steps)
$\displaystyle\fracδ{δβ_j}J(β)$ 는 방향을 결정한다. (moving directions)

ex) feature이 1개인 경우를 상정하여 유도식을 만들어 보자.

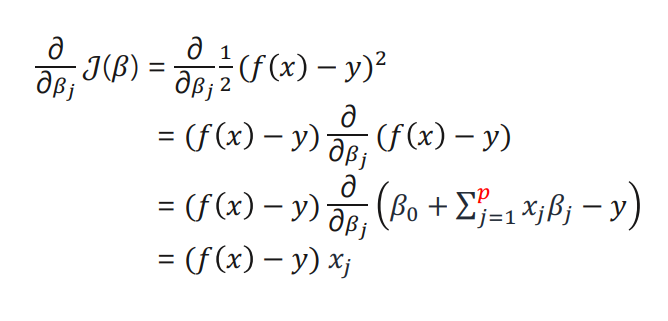
수식 다 쓰다가 화딱지 나서 그냥 캡처해 옴

Therefore, for a training sample $x$ ,
$β_j ← β_j - α\{y - f(x)\}x_j$

✔ Impact of Learning Rate

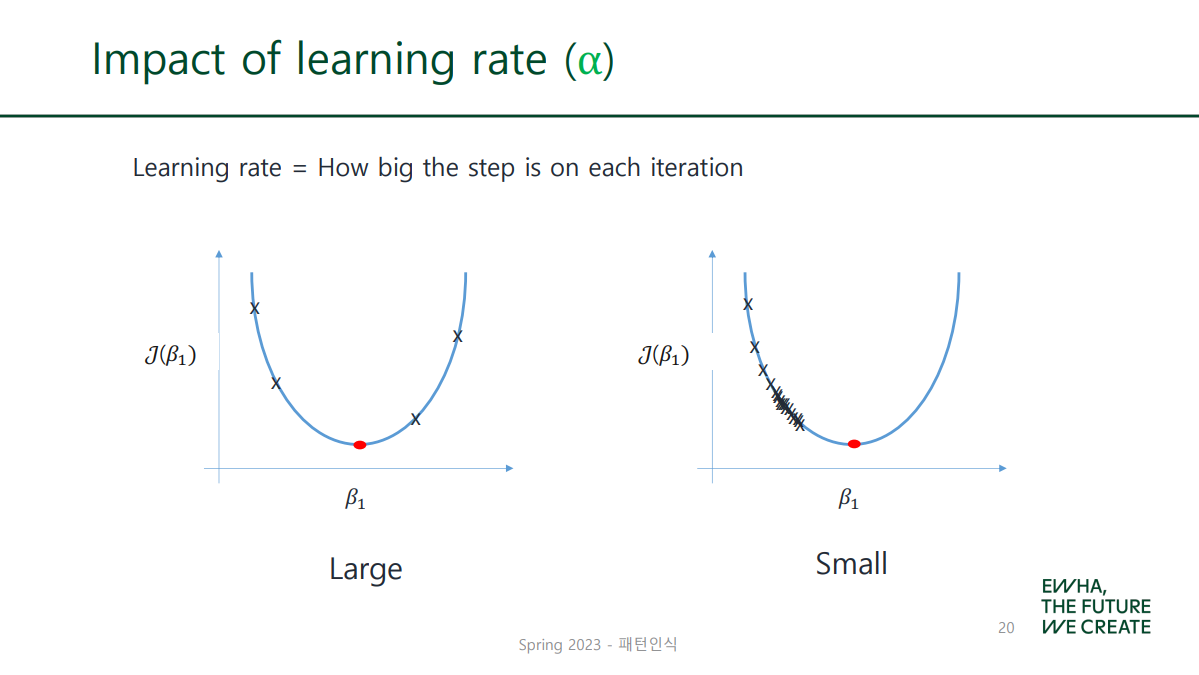
learning rate(α)가 크면 each step도 함께 커짐

✔ Impact of Derivatives

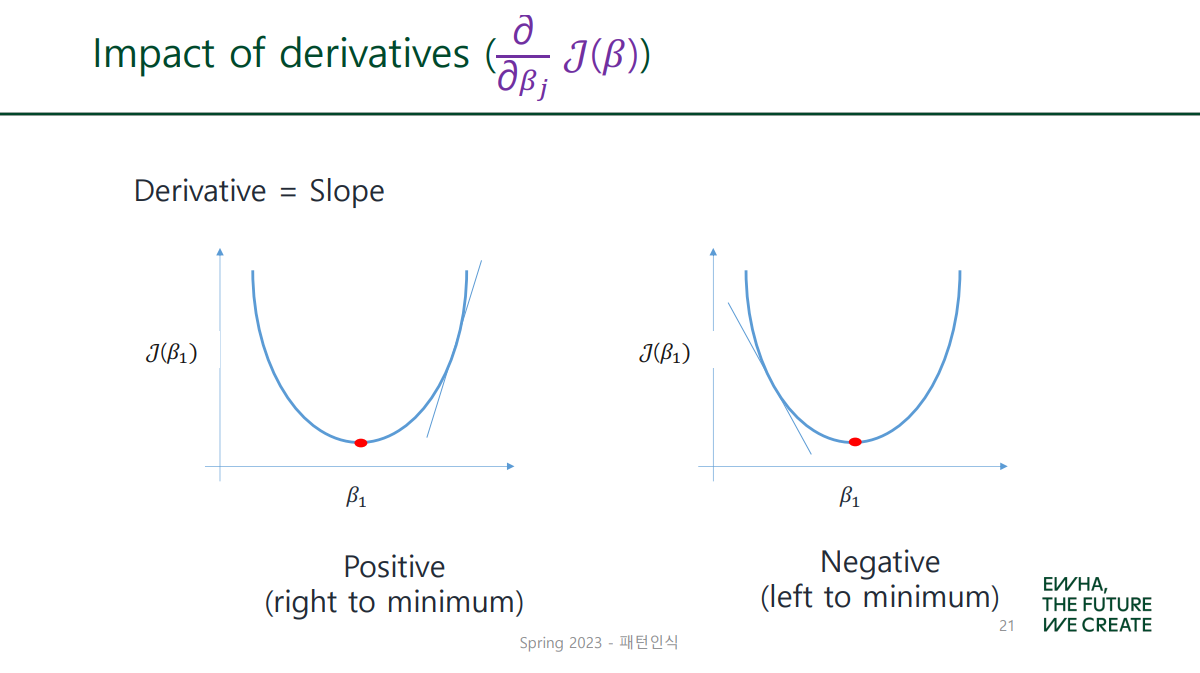
gradient descent를 두 가지로 나누자면...

✔ Stochastic Gradient Descent

Look at single sample in the training set for each iteration and update the parameters.

Therefore, for m training samples $x_1, ..., x_m$ ,
Repeatedly update $β_j$ until convergence (수렴 전까지)
for i=1 to m, $β_j ← β_j - α\{y_i - f(x_i)\}x_{ij}$

(+): 수렴속도가 빠르며(Fast Convergence), local optimal에 빠질 리스크 ↓
(-): global optimal에 도달하기 어려움. (다소 부정확함)

✔ Batch Gradient Descent

Look at every sample in the training set for each iteration and update the parameters.

Therefore, for m training samples $x_1, ..., x_m$ ,
Repeatedly update $β_j$ until convergence (수렴 전까지)
$β_j ← β_j - α\displaystyle\sum_{i=1}^{m}\{y_i - f(x_i)\}x_{ij}$

(+): 전체 데이터에 대해 업데이트가 한 번에 이루어지므로, SGD보다 상대적으로 업데이트 횟수가 적음. (Less updates)
(-): 학습이 오래 걸리고 메모리가 많이 필요함. (Resource intensive) local optimal에서 빠져나오기 힘듦.

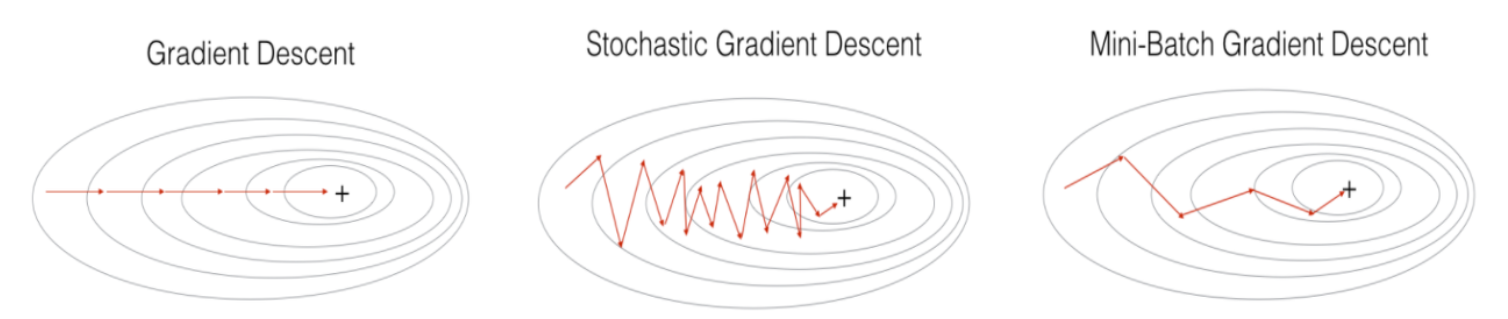
SGD가 이론적으로는 larger training set에 더 적합함

Mini-batch Gradient Descent(MSGD)는 둘의 장점을 종합한...
전체 데이터(Batch)가 아닌 일부 데이터의 모음(Mini-batch)만 사용.
근데 요새 SGD라 하면 거의 이거 말하는 거라고 하긴 하네

참고자료

242

다음 포스트