https://github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/master/DataStructure
[ 스택, 큐, 트리, 힙 구조 설명 ]
스택: 세로로 된 바구니와 같은 구조로 먼저 넣게 되는 자료가 마지막으로 나오게 되는 First-In Last-Out(FILO) 구조이다.
큐: 가로로 된 통과 같은 구조로 먼저 넣게 되는 자료가 가장 먼저 나오는 First-In First-Out(FIFO) 구조이다.
트리: 정점과 간선을 이용해 사이클을 이루지 않도록 구성한 Graph의 특수한 형태로, 계층이 있는 데이터를 표현하기에 적합하다.
힙: 최댓값 또는 최솟값을 찾아내는 연산을 쉽게 하기 위해 고안된 구조로, 각 노드의 키값이 자식의 키값보다 작지 않거나(최대힙) 그 자식의 키값보다 크지 않은(최소힙) 완전이진트리이다.
Array vs Linked List
Array(배열)
- 데이터들이 순서대로 쭉 늘어선 배열의 형식을 취함.
- 논리적 저장 순서와 물리적 저장 순서가 일치한다.
- 인덱스로 해당 원소에 접근이 가능하다. O(1)
- Random access(임의접근)가 가능하다.
- 삭제 또는 삽입의 과정 시 원소들을 shift 해줘야 하므로 시간이 오래 걸린다. O(n)
- 제한적인 크기를 갖는다.
- stack영역에 할당
Linked List(연결 리스트)
- 자료의 주소 값으로 서로 연결되어 있는 구조를 갖는다.
- 특정 원소에 접근하기 위해서는 첫 번째 원소부터 다 확인해야 해서 O(n)
- sequential access(순차접근)
- 삭제, 삽입 시 뒤로 밀거나 채우는 과정 없이 단지 주소만 서로 연결시켜 주면 되기 때문에 Array보다 빠르다. O(n)
- 맨 앞 혹은 맨 뒤에 삭제, 삽입 시 O(1)
- heap영역에 할당
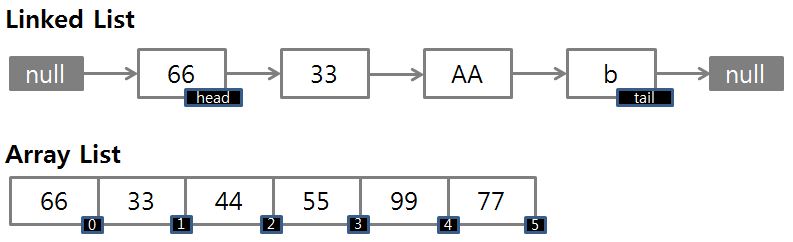
참고
https://woovictory.github.io/2018/12/27/DataStructure-Diff-of-Array-LinkedList/
https://www.nextree.co.kr/p6506/
https://www.studytonight.com/data-structures/linked-list-vs-array
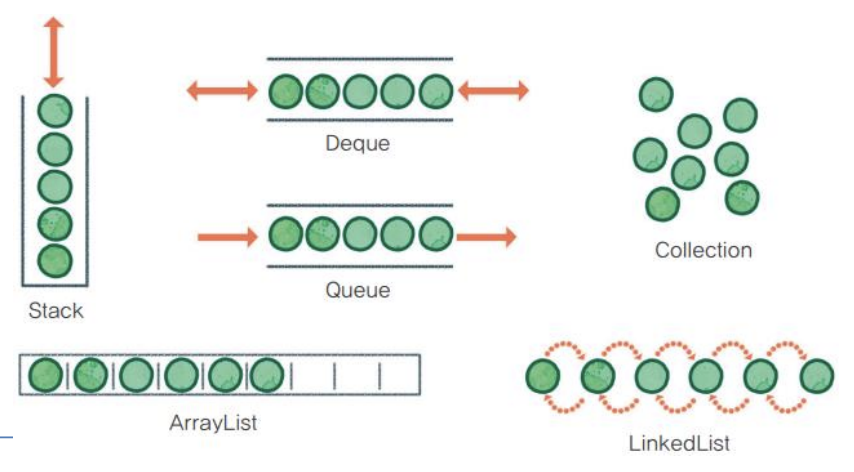
Stack & Queue
선형 자료구조의 일종
Stack
- Last In First Out (LIFO) 구조
- 나중에 들어간 원소가 먼저 나온다.
Queue
- First In First Out (FIFO) 구조
- 먼저 들어간 원소가 먼저 나온다.
Tree🌳
정점과 간선을 이용해 사이클을 이루지 않도록 구성한 Graph의 특수한 형태로, 계층이 있는 데이터를 표현하기에 적합하다.
- 비선형 자료구조
- 계층적 관계를 표현한다.
- 노드(각각의 요소)와 간선(노드간 연결)으로 이루어져있다.
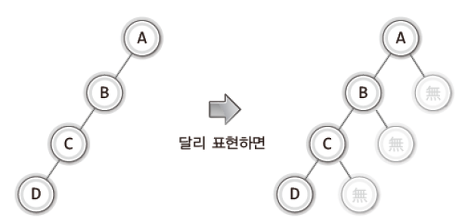
Binary Tree(이진 트리)
- 루트 노드를 중심으로 두 개의 서브 트리로 나누어진다. 나누어진 두 서브 트리도 모두 이진 트리어야 한다. (공집합도 이진 트리)
- 각 층별로 숫자를 매겨서 트리의 Level이라고 한다.
- 레벨의 값은 0부터 시작하므로 루트 노드의 레벨은 0이다.
- 트리의 최고 레벨을 트리의 height(높이)라고 한다.
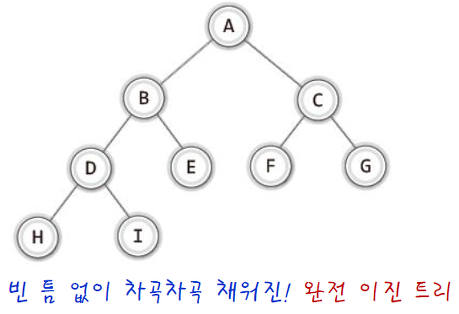
포화 이진 트리: 모든 레벨이 꽉 찬 이진 트리
완전 이진 트리: 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 차곡 채워진 이진 트리
(완전 이진 트리 < 포화 이진 트리)
BST(Binary Search Tree) 이진 탐색 트리
이진 트리 기반의 탐색을 위한 자료 구조
조건 4가지
- 모든 노드의 키는 유일하다. (중복된 데이터를 갖는 노드가 없다)
- 부모의 키가 왼쪽 자식 노드의 키보다 크다.
- 부모의 키가 오른쪽 자식 노드의 키보다 작다.
- 왼쪽, 오른쪽 서브트리도 이진 탐색 트리이다.
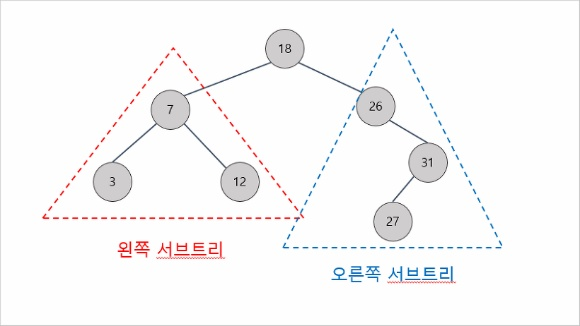
탐색, 삽입, 삭제의 평균 시간복잡도 O(log n)
But, 편향 트리는 O(n)
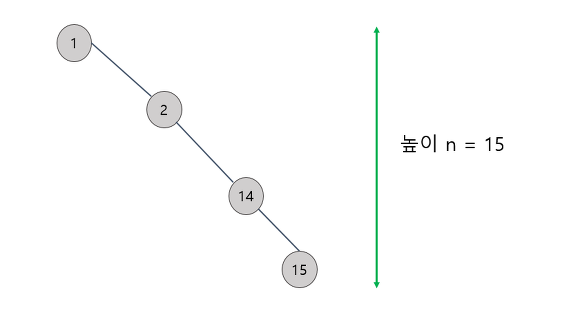
참고
https://mattlee.tistory.com/30
Heap(힙)
최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전 이진 트리를 기본으로 한 자료구조
힙에는 두가지 종류가 있으며, 부모노드의 키값이 자식노드의 키값보다 항상 큰 힙을 '최대 힙', 부모노드의 키값이 자식노드의 키값보다 항상 작은 힙을 '최소 힙'이라고 부른다.
(우선순위 큐는 힙이라는 자료구조를 가지고 구현한다.)
(우선순위 큐(Priority Queue)는 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 것)
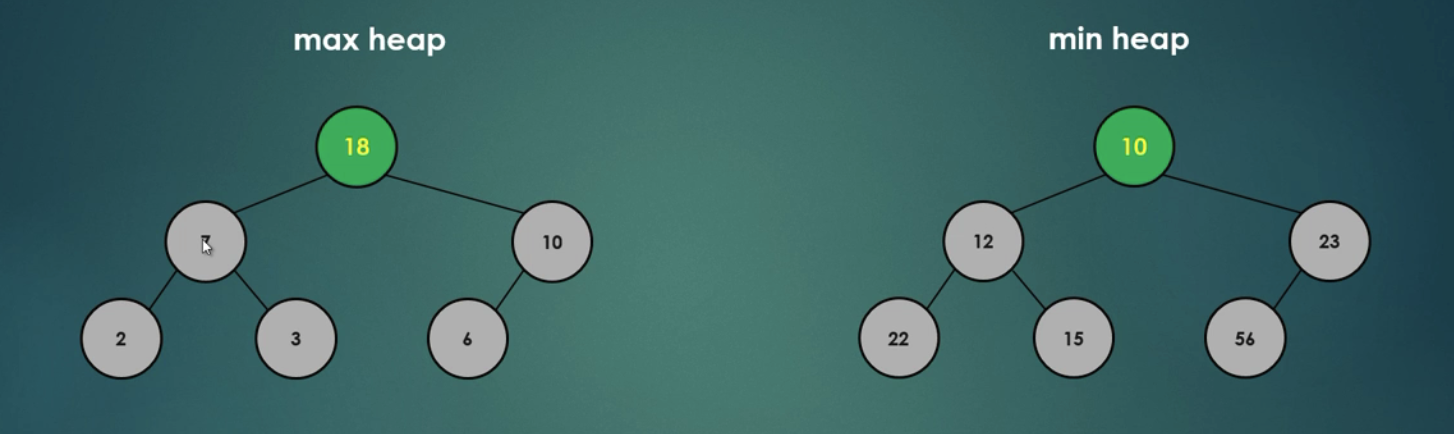
Binary Heap(이진 힙)
힙 중에서 가장 널리 쓰이는 형태 중 하나로 완전 이진 트리 형태인 힙
참고:
https://kayuse88.github.io/binary-heap/
https://doublesprogramming.tistory.com/241
Hash Table(해시테이블)
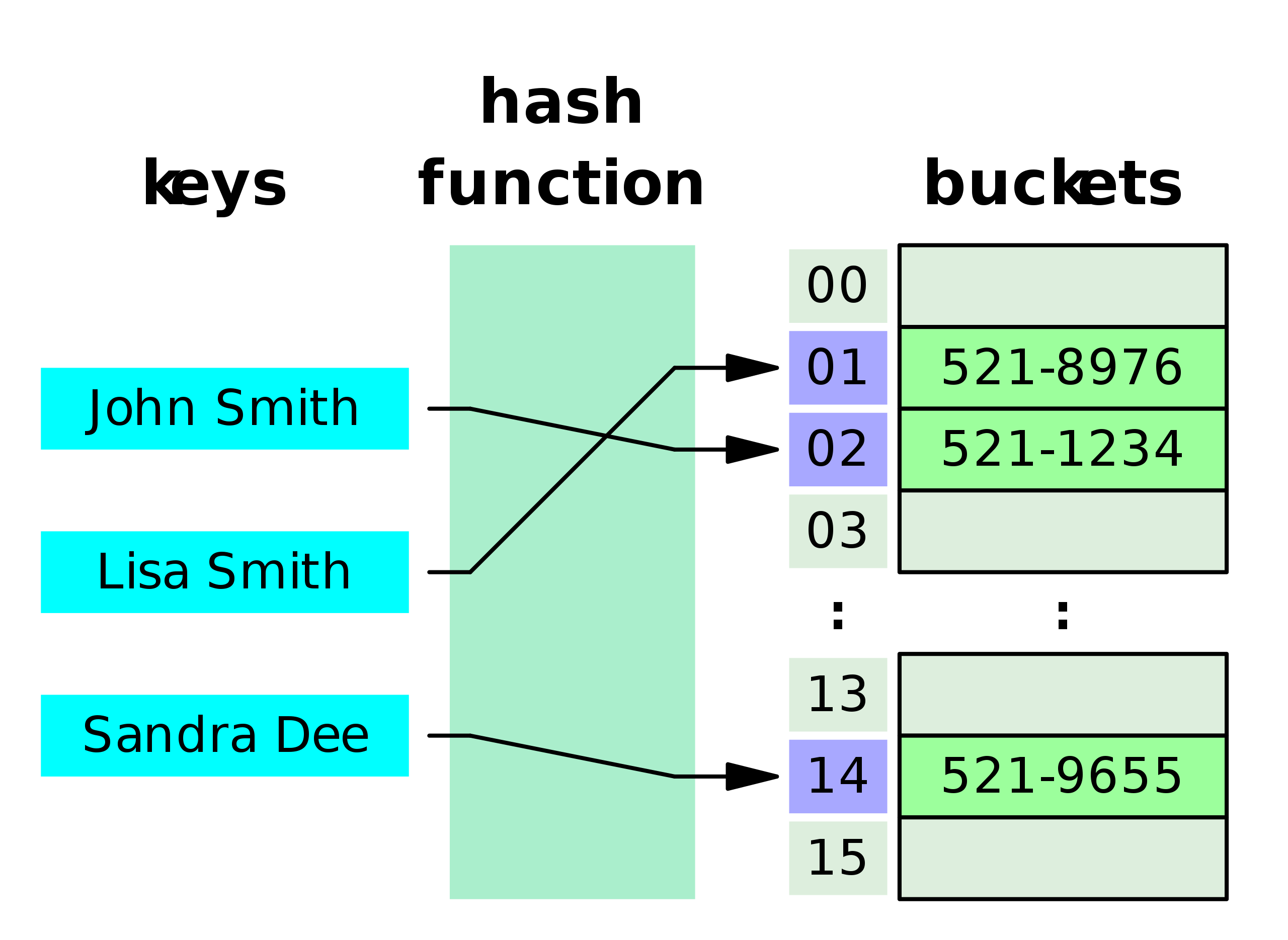
키,값으로 데이터를 저장하는 자료구조 중 하나로 빠르게 데이터를 검색할 수 있는 자료구조
내부적으로 배열을 사용하여 데이터를 저장하기 때문에 빠른 검색 속도를 갖는다.
-> 평균 시간복잡도 O(1)
(해시 테이블은 각각의 Key값에 해시함수를 적용해 배열의 고유한 index를 생성하고, 이 index를 활용해 값을 저장하거나 검색하게 된다. 여기서 실제 값이 저장되는 장소를 버킷 또는 슬롯이라고 한다.)
Hash 함수
저장할 데이터와 연관된 고유한 인덱스 값을 설정하는 것이다.
그렇지 못할 경우 Collision 발생
Resolve Collision
- Open Address 방식 (개방주소법)
- Separate Chaining 방식 (분리연결법)
참고:
https://mangkyu.tistory.com/102
Graph
노드와 간선을 하나로 모아 놓은 구조
- 트리 또한 그래프이다.
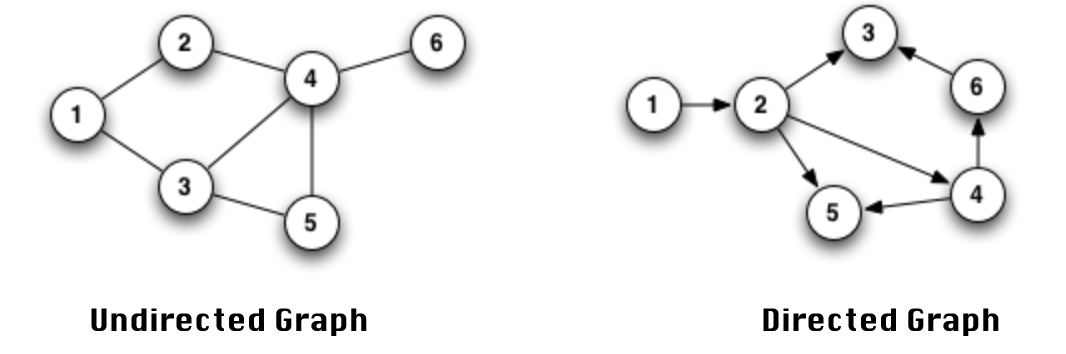
무방향 그래프와 방향 그래프
정점과 간선의 연결관계에 있어서 방향성이 없는 그래프를 Undirected Graph 라 하고, 간선에 방향성이 포함되어 있는 그래프를 Directed Graph 라고 한다.
Degree (차수)
Undirected Graph 에서 각 정점(Vertex)에 연결된 Edge 의 개수를 Degree 라 한다. Directed Graph 에서는 간선에 방향성이 존재하기 때문에 Degree 가 두 개로 나뉘게 된다.
각 정점으로부터 나가는 간선의 개수를 Outdegree 라 하고, 들어오는 간선의 개수를 Indegree 라 한다.
그래프를 구현하는 두 방법
인접 행렬 (adjacent matrix)
- 정점의 개수가 n인 그래프를 인접 행렬로 표현
- 해당하는 위치의 값을 통해 정점 간의 연결 관계를 O(1)로 파악가능
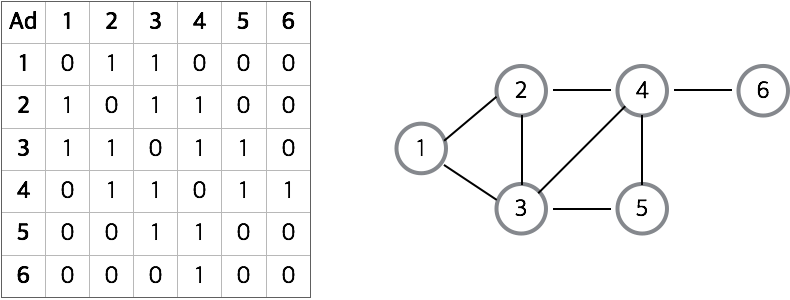
(간선의 수와 무관하게 항상 n^2개의 메모리 공간 필요)
인접 리스트 (adjacent list)
- 정점에 연결되어 있는 다른 정점들을 리스트로 표현

그래프 탐색
-
깊이 우선 탐색 (Depth First Search: DFS)
그래프 상에 존재하는 임의의 한 정점으로부터 연결되어 있는 한 정점으로만 나아간다 -
너비 우선 탐색 (Breadth First Search: BFS)
그래프 상에 존재하는 임의의 한 정점으로부터 연결되어 있는 모든 정점으로 나아간다.
