1. 학습 키워드
단순 선형 회귀, 다중 선형 회귀, 변수형 변수, 다항회귀, 스플라인회귀, 상관계수, 가설검정의 주의점
2. 학습 내용
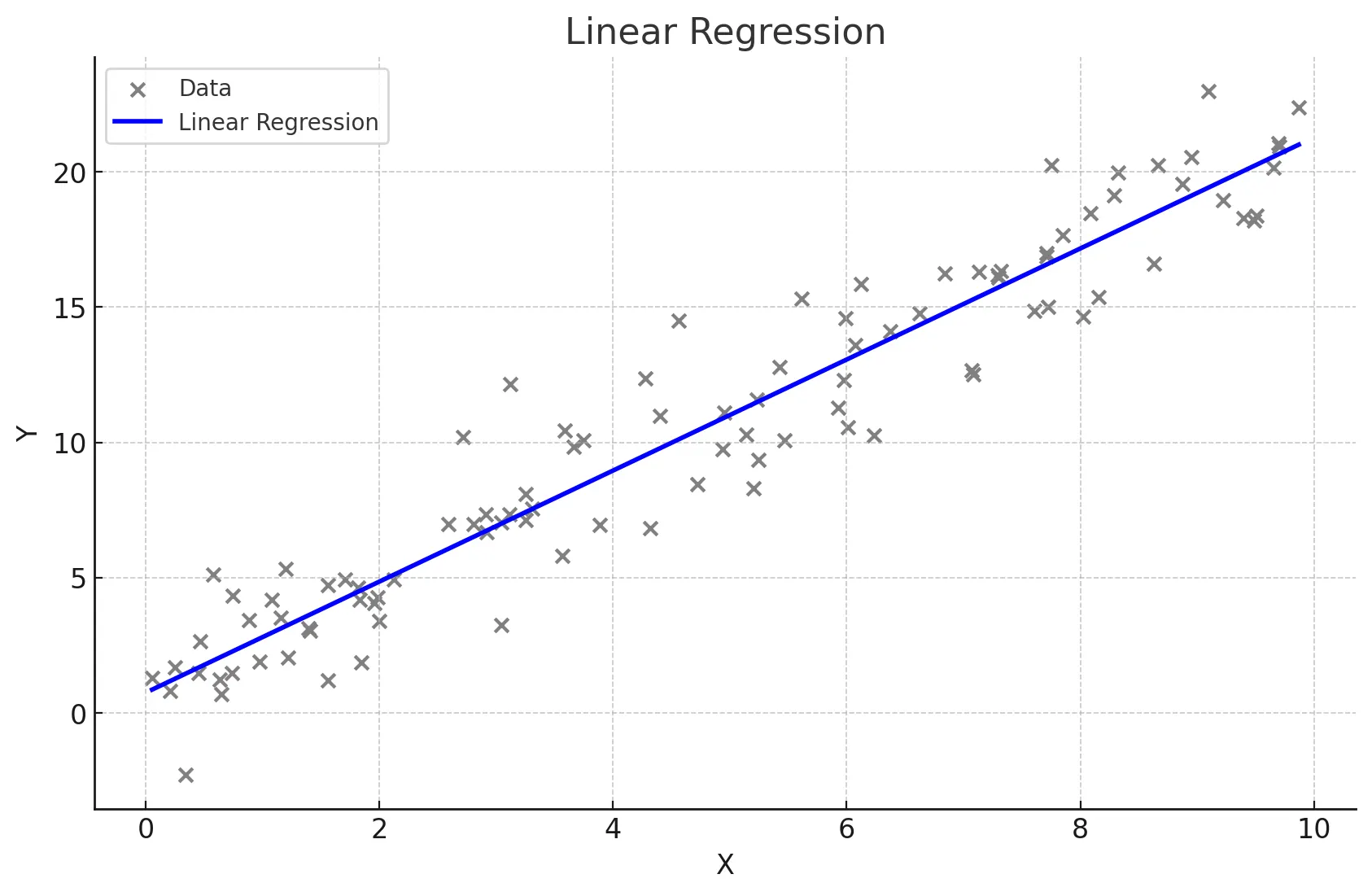
단순 선형 회귀
한개의 변수에 의한 결과 예측(= 1차 함수)
- 하나의 독립 변수(X)와 하나의 종속 변수(Y) 간의 관계를 직선으로 모델링하는 방법
다중 선형 회귀
두개 이상의 변수에 의한 결과 예측
- 두개 이상의 독립변수(X)와 하나의 종속 변수(Y) 간의 관계를 모델링
- 회귀식: Y = β0 + β1X1 + β2X2 + ... + βnXn
- 여러개의 회귀 계수가 나옴.
- 변수들간의 다중공선성 문제가 발생할 수 있다.
다중공선성
독립변수들 간의 상관관계가 높은 현상
- 독립변수들 간의 상관관계가 높으면 각 변수의 개별적 특성을 파악하기 어렵다.
- 실제 중요한 변수가 통계적으로 유의하지 않게 나타날 수 있다.
진단 방법
- 변수간 상관계수가 높은지 확인(기준은 개인 판단)
- VIF (분산 팽창계수)를 계산해 높은지 확인(10)
해결 방법
- 변수 제거
- PCA(주성분 분석)과 같은 방법으로 차원을 줄여 적용.
범주형 변수
수치형 데이터가 아니라 주로 문자형 데이터로 이루어져 있는 변수
ex) (남, 여), (서울, 대전, 대구)
순서가 있는 범주형 변수
문자를 임의의 숫자로 변환해서 사용하면 됨.
ex) 옷 사이즈(XL → 3, L → 2, s → 1)
순서가 없는 범주형 변수
원-핫 인코딩 변화을 해주어야함.
- pandas의 get_dummies를 활용해서 쉽게 구현 가능.
pd.get_dummies(df, drop_first=True)
drop_first=True를 하면 한개의 변수를 제외시킨다. 만약 3개의 변수 중에서 해당 기능으로 2개만 남기면 두개의 변수가 모두 False(=0)인 경우가 제외시킨 변수의 경우에 해당한다고 볼 수 있다. 변수를 줄여줌으로써 다중공선성도 어느정도 예방 가능.
더 쉽게 남자 컬럼만 남기면 남자가 False인 데이터컬럼은 여자인 경우의 데이터 컬럼과 같은것이다.
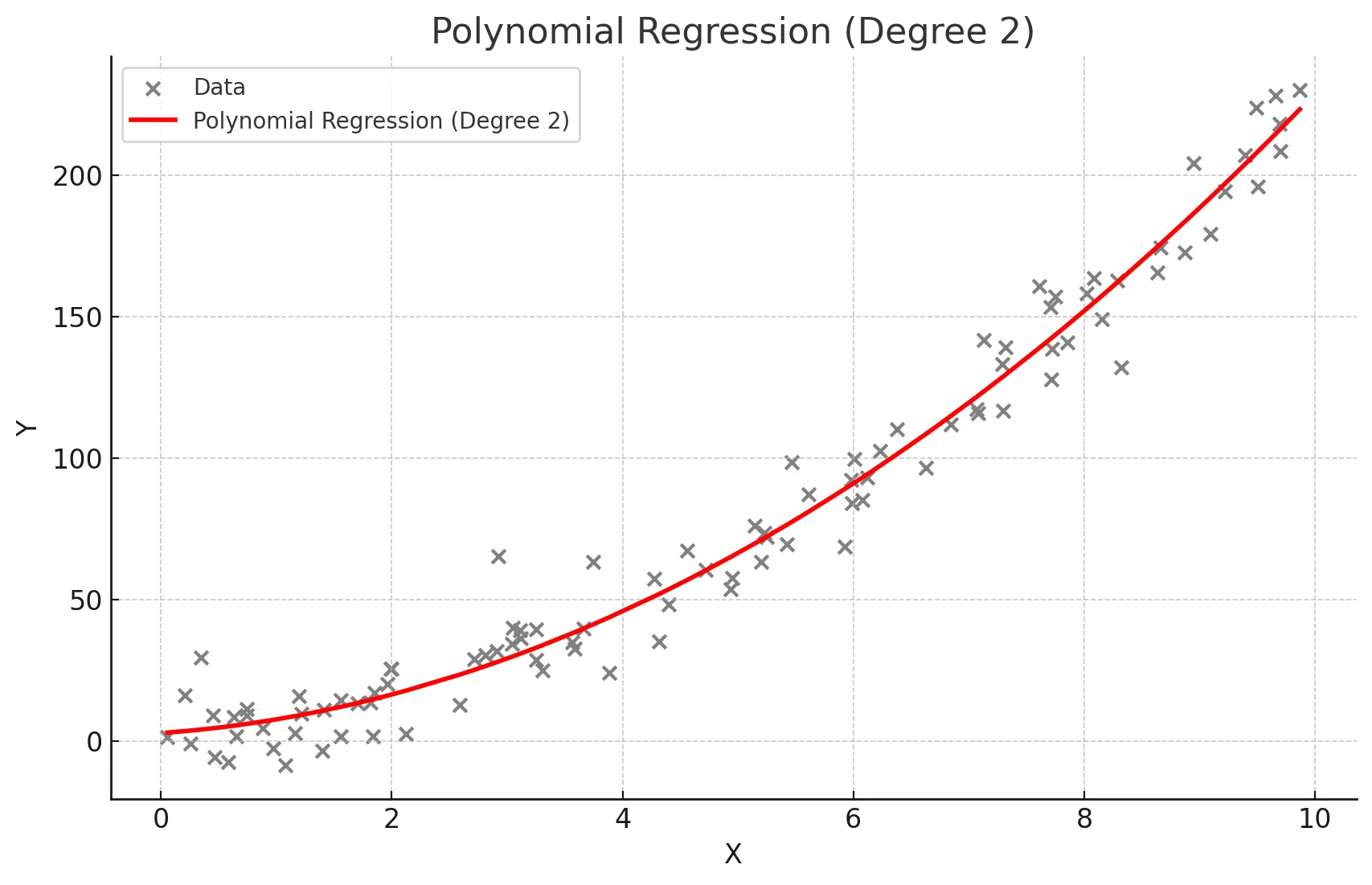
다항회귀
독립 변수와 종속 변수 간의 관계가 선형이 아닐 때 사용 (2차 함수, 3차 함수 등)
- 비선형관계를 모델링함.
- 고차 다항식의 경우 과적합 문제가 발생할 수 있다.
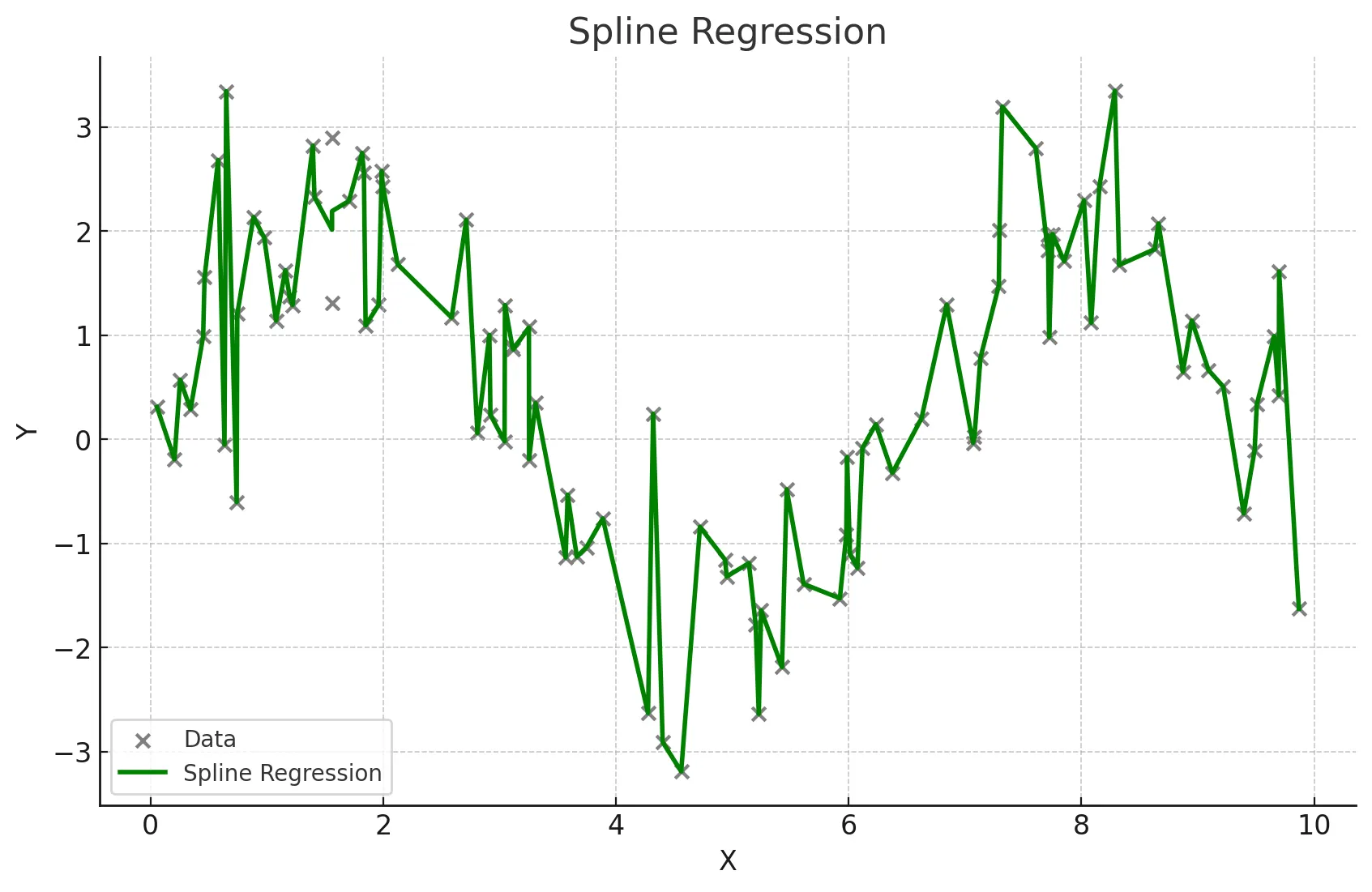
스플라인회귀
독립 변수의 구간별로 다른 회귀식을 적용해 복잡한 관계를 모델링함.
- 구간마다 다른 다항식을 사용함.
- 복잡한 비선형 관계를 유연하게 모델링할 수 있다.
상관관계 - 피어슨 상관계수
- 두 연속형 변수간의 선형관계를 측정하는 지표
- -1에서 1사이의 값을 가진다.
- *비선형 관계에서는 사용할 수 없다!!
ex) 순서형 데이터에서는 사용 못함.
상관관계 - 비모수 상관계수(순서형 데이터!!)
- 데이터가 정규분포를 따르지 않거나 변수들이 순서형 데이터일 때 사용하는 상관계수
- 스피어만 상관계수와 켄달의 타우 상관계수가 있다.
스피어만 상관계수
- 두 변수의 순위간의 상관관계를 측정할 때 사용함.
켄달의 타우 상관계수
- 두 변수간의 순위 일관성을 측정할 때 사용함.
ex) 사람의 키와 몸무게에 대해 상관계수를 알고자 할 때 키가 크고 몸무게도 더 나가면 일치 쌍에 해당, 키가 크지만 몸무게가 더 적으면 불일치 쌍에 해당 이들의 개수 비율로 상관계수를 결정
ex)
from scipy.stats import spearmanr, kendalltau# 스피어만 상관계수 계산 spearman_corr, _ = spearmanr(df['Customer Satisfaction'], df['Repurchase Intent']) # 켄달의 타우 상관계수 계산 kendall_corr, _ = kendalltau(df['Customer Satisfaction'], df['Repurchase Intent'])
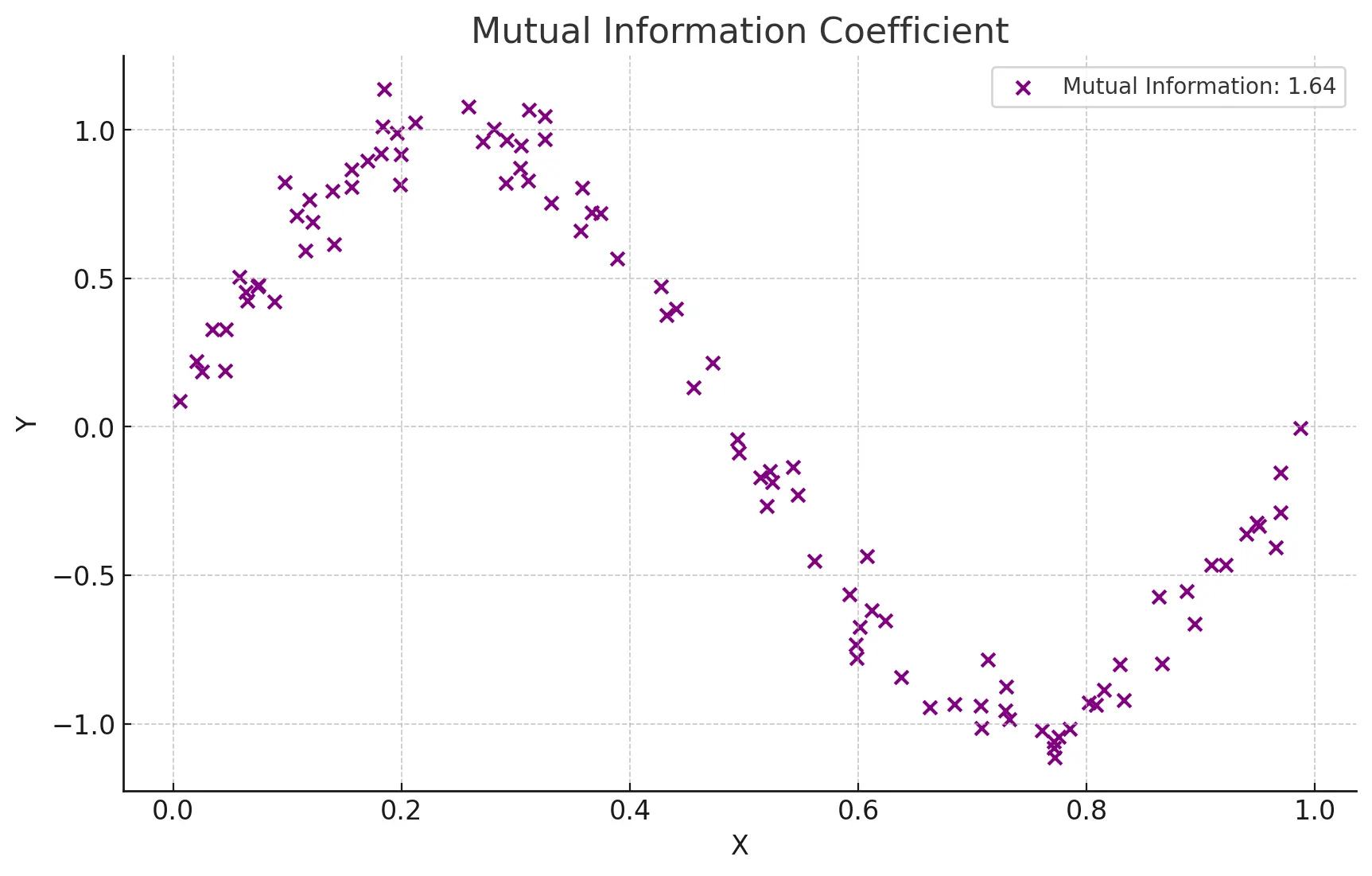
상관관계 - 상호정보 상관계수
- 변수 간의 정보 의존성을 바탕으로 비선형 관계를 탐지
- 범주형 데이터에 대해서도 적용 가능
X와 Y간의 비선형 관계를 나타냄.
언제 사용하는가?
- 두 변수가 범주형 변수일 때
- 비선형적이고 복잡한 관계를 탐지하고자 할 때
import numpy as np
from sklearn.metrics import mutual_info_score
# 범주형 예제 데이터
X = np.array(['cat', 'dog', 'cat', 'cat', 'dog', 'dog', 'cat', 'dog', 'dog', 'cat'])
Y = np.array(['high', 'low', 'high', 'high', 'low', 'low', 'high', 'low', 'low', 'high'])
# 상호 정보량 계산
mi = mutual_info_score(X, Y)
print(f"Mutual Information (categorical): {mi}")가설 검정의 주의점
재현 가능성
- 우연히 결과가 나오는 것이 아닌, 항상 일관된 결과가 나오는지 확인해야 한다.
- 재현이 되지 않는다면 내가 주장한 결과 자체가 틀릴 수 있다.
- 원하는 결과가 나올때까지 반복 실험하는 것은 좋지 않다.
- p값에 대한 논쟁도 두드러지고 있다.
- p값(유의수준)을 0.005로 설정하는 방법을 사용하기도 함.
p-해킹
- p값을 인위적으로 낮추는 행위
- 유의미한 결과를 얻기위해 다양한 변수를 시도하거나 반복 분석하는 행위
- 데이터 분석 결과의 신뢰성을 저하시킴
- 어쩌다 한번 p값이 0.05 이하로 나왔는데 이 결과만 채택하는 행위
- 결과를 보고 가설을 수정하면서 끼워 맞추는 것
선택적 보고
- 선택적응로 보고하는 것
자료수집 중단 시점 결정
- 원하는 결과가 나올 때 까지 자료를 수집하는 것을 조심!
데이터 탐색과 검증 분리
- 머신러닝을 사용할 때 검증(test)할 데이터셋을 미리 분리해놔야함.
3. 배운점
- 원-핫 인코딩 방법을 sklearn 라이브러리의 클래스 사용 방법만 있는줄 알았는데 pandas 라이브러리의 get_dummies() 함수를 사용할수도 있다는 것을 알았다.
- 상관계수를 구할때 연속형 변수가 아닌 범주형, 순서형 변수를 원-핫인코딩 해서 .corr() 함수에 적용해 사용한 경우가 종종 있었다. 그때마다 이 방법이 맞는지에 대한 의문을 했었는데 순서형 변수의 상관계수를 구하는 방법이 따로 있다는 것을 알게됐다.
- 재현 가능성에 대해 다시 한 번 생각해보게 됐다. 이전에 모델의 성능을 확인할 때 내가 원하는 성능이 나올때까지 계속 반복 실험을 한적이 있는데 이 방법이 절대 좋지 않다는 것을 다시 한 번 느꼈다.