


💡 문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.
💭 접근
먼저 이 문제를 해결하기 위해 퀸이 움직일 수 있는 방향을 알아야 한다.
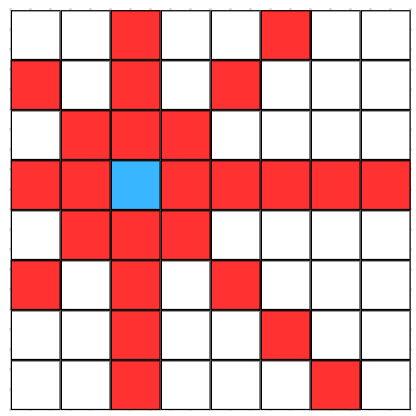
이처럼 파란색 칸에 퀸이 놓여져 있다면, 이 퀸을 기준으로 가로, 세로, 그리고 양 대각선 방향으로 이동할 수 있다.
따라서 이 문제를 해결하기 위해선 이 이동방향이 겹치지 않게 퀸을 놓는 경우의 수를 찾으면 된다.
이 문제를 처음 접했을 때는 이것이 가능한가에 대한 의문점이 먼저 들었고, 직접 예시를 찾아보며 이해할 수 있게 되었다.
아래의 n이 4일 때의 경우의 수 중 한가지를 살펴보자.
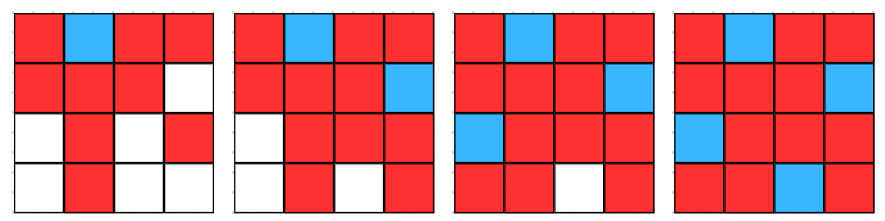
위 그림과 같은 순서로 퀸을 놓을 수 있다는 것을 이해하였고, 다음은 문제 풀이 방법이다.
우선, 퀸을 놓았을 때 퀸을 기준으로 가로, 세로, 양 대각선 방향에는 퀸을 놓지 못한다. 따라서 퀸을 놓은 좌표를 기준으로 row[i] = True, col[j] = True와 같이 간단하게 퀸이 놓여진 행과 열을 저장할 수 있다.
그렇다면 대각선 방향은 어떻게 나타낼 수 있을까?
이는 체스판의 가로 인덱스와 세로 인덱스를 활용하여 간단하게 표기할 수 있는데,
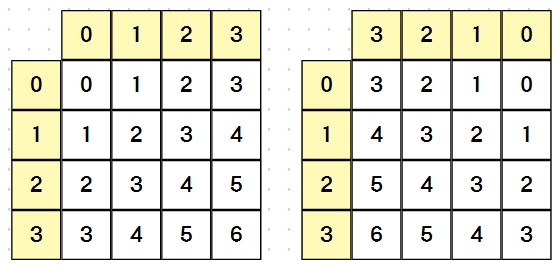
이처럼 왼쪽 대각선 방향(첫번째 그림)은 l_diag[i + j] = True로,
오른쪽 대각선 방향(두번째 그림)은 r_diag[i + (n - j - 1)] = True로 나타낼 수 있다.
이제 dfs 함수를 호출하여 백트래킹 기법을 사용해 퀸을 놓고 그 퀸을 기준으로 가로, 세로, 양 대각선 방향의 상태를 저장하며 n개의 퀸을 놓은 경우 ans에 1을 더해주면 된다.
마지막으로, 최적화를 위해 확인해야 할 것이 있는데 n x n의 체스판에 n개의 퀸을 놓기 위해선 한 행에 반드시 하나의 퀸이 놓여져야 하기 때문에 만약 어떤 행에 퀸을 놓지 않고 다음 열에 퀸을 놓는 경우는 제외해주어야 한다.
📒 코드
def dfs(depth):
global ans
if depth == n:
ans += 1
return
for i in range(n):
if i == depth: # 한 행에 반드시 하나의 퀸을 놓아야한다.
for j in range(n):
if not row[i] and not col[j] and not l_diag[i + j] and not r_diag[i + (n - j - 1)]:
row[i] = True
col[j] = True
l_diag[i + j] = True
r_diag[i + (n - j - 1)] = True
dfs(depth + 1)
row[i] = False
col[j] = False
l_diag[i + j] = False
r_diag[i + (n - j - 1)] = False
n = int(input())
row = [False for _ in range(n)]
col = [False for _ in range(n)]
l_diag = [False for _ in range(n * 2 - 1)]
r_diag = [False for _ in range(n * 2 - 1)]
ans = 0
dfs(0)
print(ans)💭 후기
python3로 제출했을 때 시간초과가 발생하였고, pypy3로 제출하여 성공을 받았다. 찾아본 결과 python3로 제출할 경우 변수 선언 위치같은 사소한 것에 따라서도 성공/시간초과가 갈리는 빡빡한 문제였다.
🔗 문제 출처
https://www.acmicpc.net/problem/9663
