[백준] 11664번 선분과 점 - Python / 알고리즘 중급 1/3 - 이분 탐색

ByungJik_Oh·2025년 7월 14일

Baekjoon Online Judge

[Baekjoon Online Judge]

목록 보기

194/244

💡 문제

3차원 좌표 평면 위에 선분 하나와 점 하나가 있다. 선분의 양 끝점은 A(Ax, Ay, Az)와 B(Bx, By, Bz)로 나타낼 수 있다. 점의 좌표는 C(Cx, Cy, Cz) 이다.

선분과 점 사이의 거리의 최솟값을 구하는 프로그램을 작성하시오.

두 점 (x1, y1, z1)과 (x2, y2, z2) 사이의 거리는 $\sqrt{(x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2}$ 이다.

입력

첫째 줄에 선분과 점의 좌표 Ax, Ay, Az, Bx, By, Bz, Cx, Cy, Cz가 주어진다. 좌표는 0보다 크거나 같고, 10,000보다 작거나 같은 정수이다.

출력

첫째 줄에 선분과 점 사이의 거리의 최솟값을 출력한다. 절대/상대 오차는 10 $^{-6}$ 까지 허용한다.

💭 접근

이 문제는 이분 탐색 문제로 분류되어 있지만 헤론의 공식(Heron's Formula)를 활용하면 더 쉽게 해결할 수 있다.

Heron's\;Formula

S=\sqrt{s(s-a)(s-b)(s-c)},\;s=\frac{a+b+c}{2}

위 공식은 삼각형의 세 변의 길이를 알고 있을 때 삼각형의 넓이를 구하는 공식이다.

그렇다면 이 공식을 어떻게 적용할 수 있을까?

이 문제는 3가지 경우로 나눌 수 있다.

점 A, B, C 가 같은 선분 상에 있고, BC의 길이가 AC와 AB를 더한 길이보다 크거나 같을 때

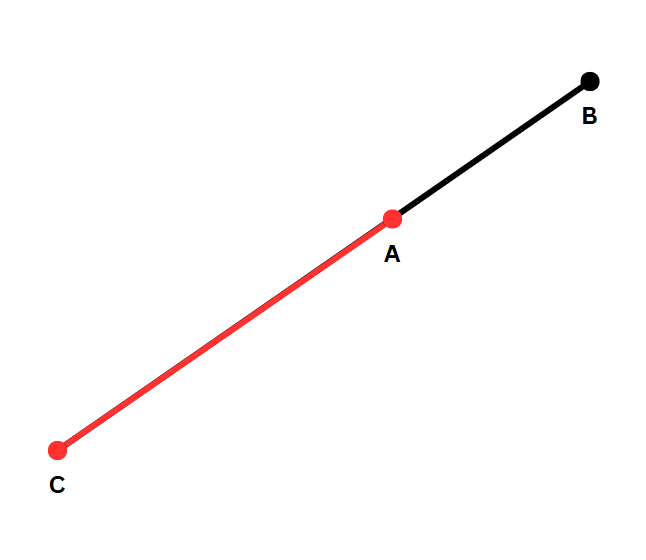
위와 같은 상황으로, 이때는 AC의 길이가 정답이 된다.

점 A, B, C 가 같은 선분 상에 있고, AC의 길이가 AB와 BC를 더한 길이보다 크거나 같을 때

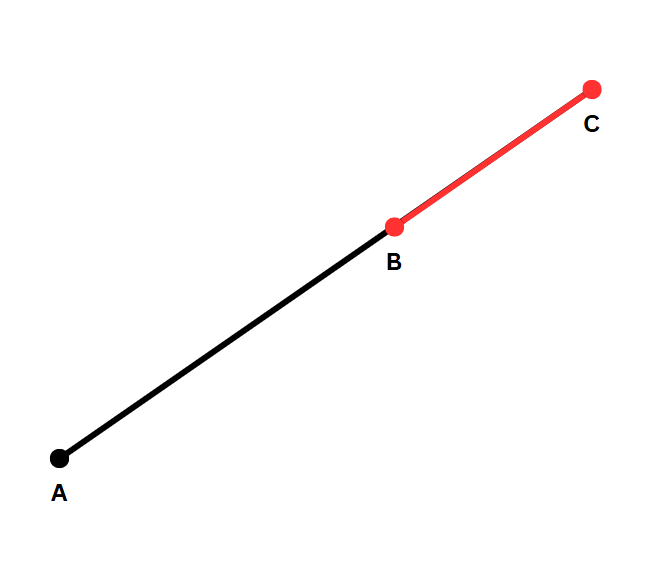
위와 같은 상황으로, 이때는 BC의 길이가 정답이 된다.

점 A, B, C가 같은 선분 상에 존재하지 않고, 삼각형을 이루고 있을 때

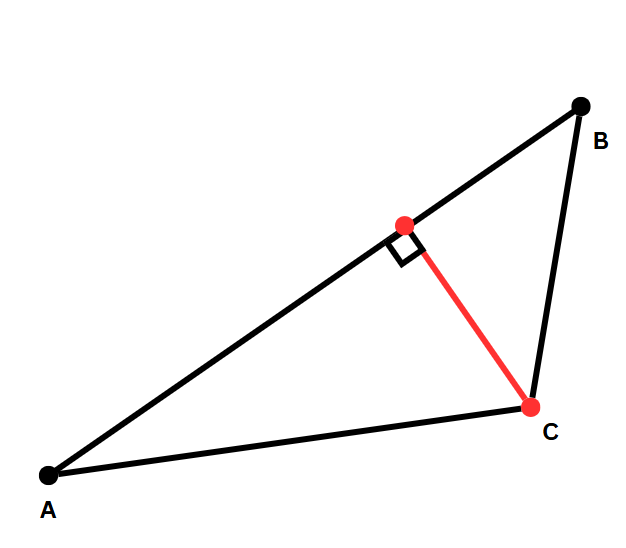
이때 헤론의 공식을 적용할 수 있는데, 각 점이 이루는 세개의 선분의 길이를 이용하여 세 선분이 이루는 삼각형의 넓이를 구한 뒤, 선분 AB를 밑변으로 넓이에서 나눠주면 점 C에서 선분 AB까지 제일 가까운 길이를 구할 수 있다. (삼각형의 높이)

📒 코드

def calculate_len(x1, x2, y1, y2, z1, z2):
    return ((x1 - x2)**2 + (y1 - y2)**2 + (z1 - z2)**2)**0.5

def calculate_area(len1, len2, len3):
    s = (len1 + len2 + len3) / 2
    return (s * (s - len1) * (s - len2) * (s - len3))**0.5

ax, ay, az, bx, by, bz, cx, cy, cz = map(int, input().split())
len_ab = calculate_len(ax, bx, ay, by, az, bz)
len_ac = calculate_len(ax, cx, ay, cy, az, cz)
len_bc = calculate_len(bx, cx, by, cy, bz, cz)

if round(len_bc**2, 6) >= round(len_ab**2, 6) + round(len_ac**2, 6):
    print(f'{len_ac:.10f}')
elif round(len_ac**2, 6) >= round(len_ab**2, 6) + round(len_bc**2, 6):
    print(f'{len_bc:.10f}')
else:
    area = calculate_area(len_ab, len_ac, len_bc)
    print(f'{(2 * area / len_ab):.10f}')