


💡 문제
아래의 그림과 같이 높은 빌딩 사이를 따라 좁은 길이 나있다. 두 개의 사다리가 있는데 길이가 x인 사다리는 오른쪽 빌딩의 아래를 받침대로 하여 왼쪽 빌딩에 기대져 있고 길이가 y인 사다리는 왼쪽 빌딩의 아래를 받침대로 하여 오른쪽 빌딩에 기대져 있다. 그리고 두 사다리는 땅에서부터 정확하게 c인 지점에서 서로 교차한다. 그렇다면 두 빌딩은 얼마나 떨어져 있는 걸까?

입력
첫째 줄에 차례대로 x, y, c에 해당하는 양의 실수 세 개가 입력된다. 수는 소수점 여섯째 자리까지 주어질 수 있으며, 3,000,000,000보다 작거나 같다.
출력
두 빌딩사이에 너비가 되는 수치를 출력한다. 절대/상대 오차는 10까지 허용한다.
💭 접근
이 문제는 구해야하는 밑변의 길이를 임의로 설정하고, 이때 선분이 만나는 지점에서의 높이를 비교하며 해결하는 문제이다.
또한, 이 문제는 닮은 꼴 개념을 알고 활용할 줄 알아야 해결할 수 있다. 아래 그림을 살펴보자.
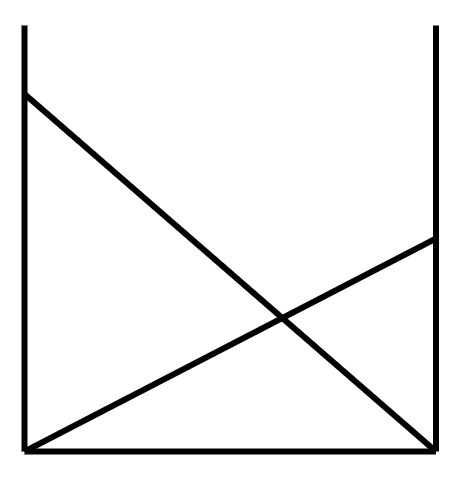
만약 사다리가 위와 같이 놓여있다고 가정했을때,
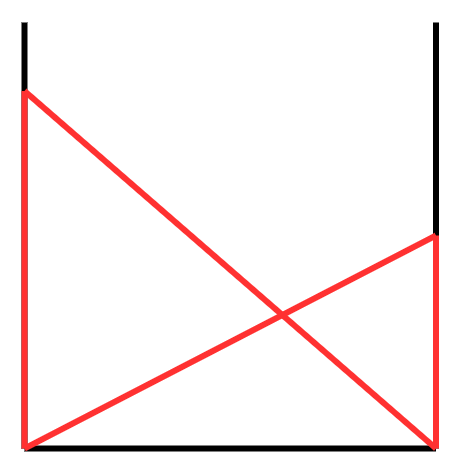
이처럼 빨간선으로 이루어진 두 삼각형은 닮은 꼴이고,
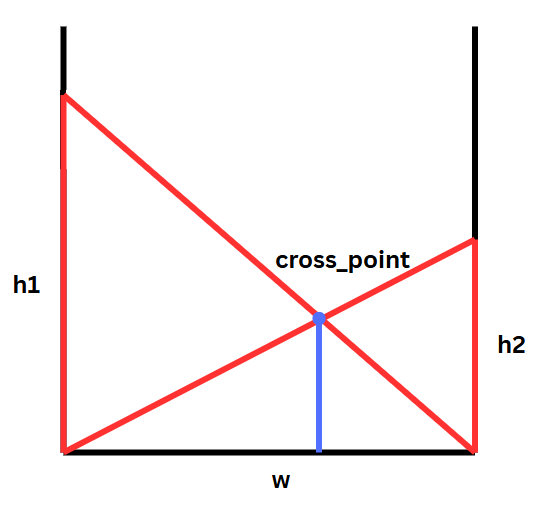
이를 활용하여 접점(cross_point)은 다음과 같이 구할 수 있다.
cross_point = w x h1 / (h1 + h2)
그렇다면 이 개념을 적용하여 문제를 해결해보자.
먼저 밑변의 최대 길이는 아래 그림과 같이 x와 y의 최소값보다 클 수 없다. 또한 최소길이는 0보다는 작아질 수 없다.
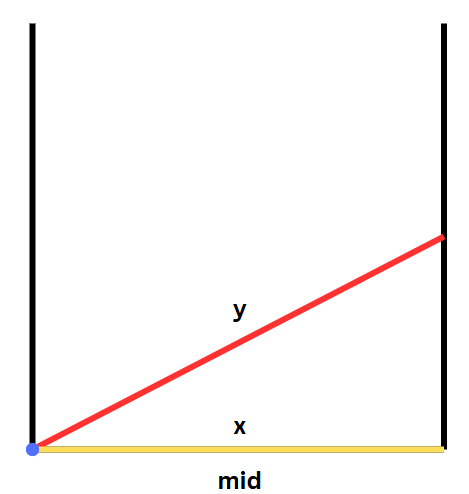
이 상태에서 밑변의 길이를 줄여보자.
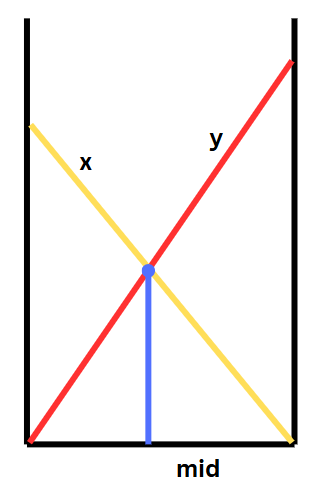
그러면 이처럼 완전히 누워있던 x 사다리가 세워지게되고, 이처럼 y 사다리와의 접점이 생기게 된다. 이때 위에서 말했던 닯은 꼴의 성질을 이용하여 파란색 선의 길이를 구할 수 있다.
그렇다면 방금 구한 파란색 선의 길이가 입력으로 주어진 c보다 크다면 mid를 늘려 파란색 선의 길이를 줄이면 되고,
반대로 파란색 선의 길이가 입력으로 주어진 c보다 작다면 mid를 더 줄여 파란색 선의 길이를 늘리면 된다.
이때 유의할 점으론 이전 문제들과 다르게 정수가 아닌 실수를 구해야 하므로 이전의 mid값을 소수점 넷째자리(오차 허용 범위가 10 이므로)에서 반올림한 값과 현제 mid값을 반올림한 값과 같다면 정답을 출력해주면 된다. 그렇지 않으면 시간초과가 발생할 수 있다.
📒 코드
def binary_search():
start = 0
end = min(x, y)
prev_mid = 0
while start <= end:
mid = (start + end) / 2
xh = (x**2 - mid**2)**0.5
yh = (y**2 - mid**2)**0.5
cross_point = mid * xh / (xh + yh)
h = round(yh * cross_point / mid, 3)
if h == c or prev_mid == round(mid, 3):
return round(mid, 3)
elif h > c:
start = mid
prev_mid = round(mid, 3)
elif h < c:
end = mid
prev_mid = round(mid, 3)
x, y, c = map(float, input().split())
print(f'{binary_search():.3f}')💭 후기
이때까지는 정답이 정수로 딱 떨어지는 문제만 풀다가 실수 값을 찾아야하는 문제라서 마지막 정답을 출력할 때 조금 고민했던 문제였다.
🔗 문제 출처
https://www.acmicpc.net/problem/2022
