[백준] 14500번 테트로미노 - Python / 알고리즘 기초 2/2 - 브루트 포스

ByungJik_Oh·2025년 4월 4일

Baekjoon Online Judge

[Baekjoon Online Judge]

목록 보기

72/244

💡 문제

폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.

정사각형은 서로 겹치면 안 된다.
도형은 모두 연결되어 있어야 한다.
정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.

정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.

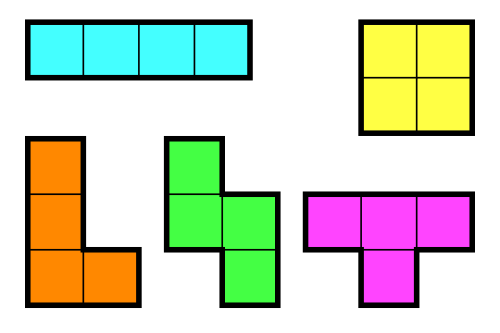
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.

테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.

테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.

입력

첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)

둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.

출력

첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.

💭 접근

우선 각 테트로미노들은 3x2, 2x3, 1x4, 4x1, 2x2 모양으로 이루어져 있고, 이를 숫자 배열 위에 올려서 이동시키면서 그 안에 속한 숫자들의 합을 구한다고 생각하면 쉽다.

각 테트로미노들이 공통적으로 속하는 점을 기준으로 잡고, 그 좌표를 기준으로 도형을 그리면 된다. 그림과 함께 살펴보자. (빨간색 네모가 기준)

2x3, 기준 : (0, 1)

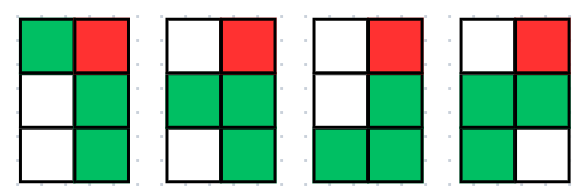
이를 코드로 작성해보면 아래와 같이 작성할 수 있다.

num[i][j - 1] + num[i][j] + num[i + 1][j] + num[i + 2][j]
num[i + 1][j - 1] + num[i][j] + num[i + 1][j] + num[i + 2][j]
num[i + 2][j - 1] + num[i][j] + num[i + 1][j] + num[i + 2][j]
num[i + 1][j - 1] + num[i + 2][j - 1] + num[i][j] + num[i + 1][j]

하지만 이들을 좌우반전시킨 모양도 있는데,

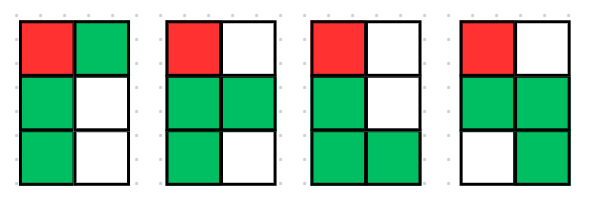
이처럼 그릴 수 있고, 이들은 모양을 따로 그리는 것이 아닌 숫자 배열을 좌우로 반전시켜서 동일한 모양에 대해 값을 구하면 된다.

lrnum[i][j - 1] + lrnum[i][j] + lrnum[i + 1][j] + lrnum[i + 2][j]
lrnum[i + 1][j - 1] + lrnum[i][j] + lrnum[i + 1][j] + lrnum[i + 2][j]
lrnum[i + 2][j - 1] + lrnum[i][j] + lrnum[i + 1][j] + lrnum[i + 2][j]
lrnum[i + 1][j - 1] + lrnum[i + 2][j - 1] + lrnum[i][j] + lrnum[i + 1][j]

3x2, 기준 : (0, 2)

이를 코드로 작성해보면 아래와 같이 작성할 수 있다.

num[i][j - 2] + num[i][j - 1] + num[i][j] + num[i + 1][j]
num[i][j - 2] + num[i][j - 1] + num[i + 1][j - 1] + num[i][j]
num[i][j - 2] + num[i + 1][j - 2] + num[i][j - 1] + num[i][j]
num[i + 1][j - 2] + num[i + 1][j - 1] + num[i][j - 1] + num[i][j]

이 또한 위아래로 반전시킨 모양도 있다.

마찬가지로, 도형을 상하반전시키는 것이 아닌 숫자 배열을 위아래로 반전시켜 동일한 모양에 대해 값을 구한다.

udnum[i][j - 2] + udnum[i][j - 1] + udnum[i][j] + udnum[i + 1][j]
udnum[i][j - 2] + udnum[i][j - 1] + udnum[i + 1][j - 1] + udnum[i][j]
udnum[i][j - 2] + udnum[i + 1][j - 2] + udnum[i][j - 1] + udnum[i][j]
udnum[i + 1][j - 2] + udnum[i + 1][j - 1] + udnum[i][j - 1] + udnum[i][j]

1x4, 기준 : (0, 3) / 4x1, 기준 (0, 0) / 2x2, 기준 (0, 1)

이를 코드로 작성해보면 아래와 같이 작성할 수 있다.

num[i][j - 3] + num[i][j - 2] + num[i][j - 1] + num[i][j] # 1*4
num[i][j] + num[i + 1][j] + num[i + 2][j] + num[i + 3][j] # 4*1
num[i][j - 1] + num[i][j] + num[i + 1][j - 1] + num[i + 1][j] # 2*2

이러한 모양들은 상하좌우 반전을 해도 같은 모양이기 때문에 반전을 시킬 필요가 없다.

📒 코드

n, m = map(int, input().split())
num = [list(map(int, input().split())) for _ in range(n)]
udnum = num[::-1]
lrnum = [num[i][::-1] for i in range(n)]
ans = 0

for i in range(n - 2): # 3*2
    for j in range(1, m):
        temp = []
        temp.append(num[i][j - 1] + num[i][j] + num[i + 1][j] + num[i + 2][j])
        temp.append(lrnum[i][j - 1] + lrnum[i][j] + lrnum[i + 1][j] + lrnum[i + 2][j]) 
        temp.append(num[i + 1][j - 1] + num[i][j] + num[i + 1][j] + num[i + 2][j])
        temp.append(lrnum[i + 1][j - 1] + lrnum[i][j] + lrnum[i + 1][j] + lrnum[i + 2][j]) 
        temp.append(num[i + 2][j - 1] + num[i][j] + num[i + 1][j] + num[i + 2][j])
        temp.append(lrnum[i + 2][j - 1] + lrnum[i][j] + lrnum[i + 1][j] + lrnum[i + 2][j])
        temp.append(num[i + 1][j - 1] + num[i + 2][j - 1] + num[i][j] + num[i + 1][j])
        temp.append(lrnum[i + 1][j - 1] + lrnum[i + 2][j - 1] + lrnum[i][j] + lrnum[i + 1][j])
        ans = max(ans, max(temp))
for i in range(n - 1): # 2*3
    for j in range(2, m):
        temp = []
        temp.append(num[i][j - 2] + num[i][j - 1] + num[i][j] + num[i + 1][j])
        temp.append(udnum[i][j - 2] + udnum[i][j - 1] + udnum[i][j] + udnum[i + 1][j])
        temp.append(num[i][j - 2] + num[i][j - 1] + num[i + 1][j - 1] + num[i][j])
        temp.append(udnum[i][j - 2] + udnum[i][j - 1] + udnum[i + 1][j - 1] + udnum[i][j])
        temp.append(num[i][j - 2] + num[i + 1][j - 2] + num[i][j - 1] + num[i][j])
        temp.append(udnum[i][j - 2] + udnum[i + 1][j - 2] + udnum[i][j - 1] + udnum[i][j])
        temp.append(num[i + 1][j - 2] + num[i + 1][j - 1] + num[i][j - 1] + num[i][j])
        temp.append(udnum[i + 1][j - 2] + udnum[i + 1][j - 1] + udnum[i][j - 1] + udnum[i][j])
        ans = max(ans, max(temp))
for i in range(n): # 1*4
    for j in range(3, m):
        ans = max(ans, num[i][j - 3] + num[i][j - 2] + num[i][j - 1] + num[i][j])
for i in range(n - 3): # 4*1
    for j in range(m):
        ans = max(ans, num[i][j] + num[i + 1][j] + num[i + 2][j] + num[i + 3][j])
for i in range(n - 1): # 2*2
    for j in range(1, m):
        ans = max(ans, num[i][j - 1] + num[i][j] + num[i + 1][j - 1] + num[i + 1][j])

print(ans)