


💡 문제
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선이 같은 위치를 갖는다. 아래 그림은 N = 5, H = 6 인 경우의 그림이고, 가로선은 없다.

초록선은 세로선을 나타내고, 초록선과 점선이 교차하는 점은 가로선을 놓을 수 있는 점이다. 가로선은 인접한 두 세로선을 연결해야 한다. 단, 두 가로선이 연속하거나 서로 접하면 안 된다. 또, 가로선은 점선 위에 있어야 한다.
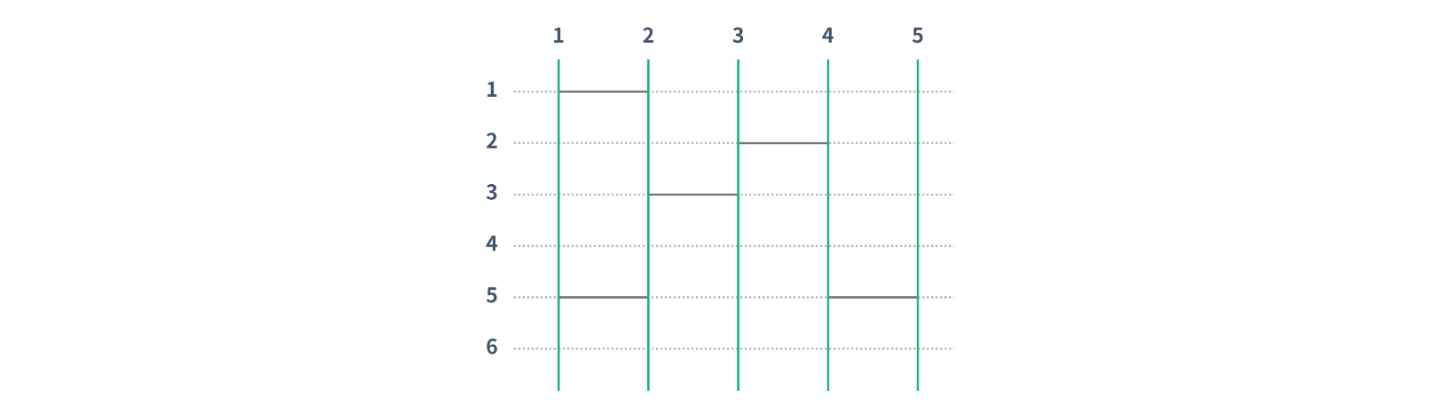
위의 그림에는 가로선이 총 5개 있다. 가로선은 위의 그림과 같이 인접한 두 세로선을 연결해야 하고, 가로선을 놓을 수 있는 위치를 연결해야 한다.
사다리 게임은 각각의 세로선마다 게임을 진행하고, 세로선의 가장 위에서부터 아래 방향으로 내려가야 한다. 이때, 가로선을 만나면 가로선을 이용해 옆 세로선으로 이동한 다음, 이동한 세로선에서 아래 방향으로 이동해야 한다.
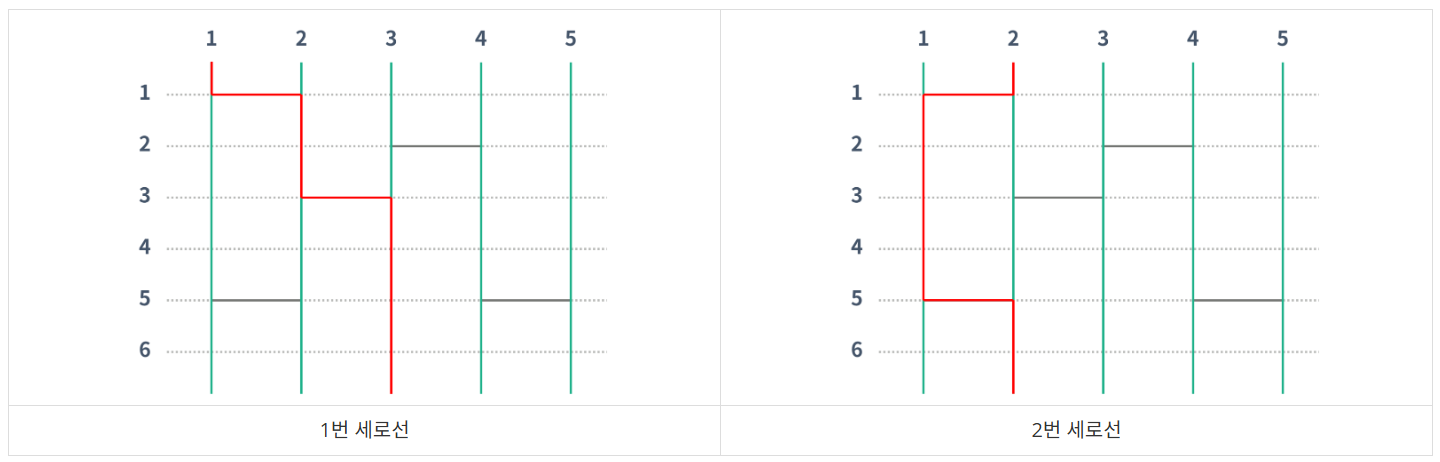
위의 그림에서 1번은 3번으로, 2번은 2번으로, 3번은 5번으로, 4번은 1번으로, 5번은 4번으로 도착하게 된다. 아래 두 그림은 1번과 2번이 어떻게 이동했는지 나타내는 그림이다.
사다리에 가로선을 추가해서, 사다리 게임의 결과를 조작하려고 한다. 이때, i번 세로선의 결과가 i번이 나와야 한다. 그렇게 하기 위해서 추가해야 하는 가로선 개수의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 세로선의 개수 N, 가로선의 개수 M, 세로선마다 가로선을 놓을 수 있는 위치의 개수 H가 주어진다. (2 ≤ N ≤ 10, 1 ≤ H ≤ 30, 0 ≤ M ≤ (N-1)×H)
둘째 줄부터 M개의 줄에는 가로선의 정보가 한 줄에 하나씩 주어진다.
가로선의 정보는 두 정수 a과 b로 나타낸다. (1 ≤ a ≤ H, 1 ≤ b ≤ N-1) b번 세로선과 b+1번 세로선을 a번 점선 위치에서 연결했다는 의미이다.
가장 위에 있는 점선의 번호는 1번이고, 아래로 내려갈 때마다 1이 증가한다. 세로선은 가장 왼쪽에 있는 것의 번호가 1번이고, 오른쪽으로 갈 때마다 1이 증가한다.
입력으로 주어지는 가로선이 서로 연속하는 경우는 없다.
출력
i번 세로선의 결과가 i번이 나오도록 사다리 게임을 조작하려면, 추가해야 하는 가로선 개수의 최솟값을 출력한다. 만약, 정답이 3보다 큰 값이면 -1을 출력한다. 또, 불가능한 경우에도 -1을 출력한다.
💭 접근
이 문제는 추가할 수 있는 가로선을 걸러내고, 백트래킹으로 추가할 수 있는 가로선을 모두 추가해 본 뒤, 각각의 경우 직접 사다리 타기 로직을 구현하여 문제에서 주어진 조건을 만족할 수 있는지 확인해야하는 문제이다.
이 문제를 해결하기 위해 다음과 같은 순서를 따른다.
- 먼저 사다리를 입력 받을 때, 각 가로선은
b번 세로선과b + 1세로선을a가로선에서 연결한다는 의미이므로 상호간의 연결을 나타내기 위해 그래프 형태로 입력받아야 한다.
ladders = [[] for _ in range(n + 2)]
for _ in range(m):
a, b = map(int, input().split())
ladders[b].append([b + 1, a])
ladders[b + 1].append([b, a])위 코드처럼 2차원의 빈 공간에 각 세로선이 어떤 가로선에 의해 이어지는지 저장한다.
이렇게 해야 뒤에 직접 사다리 타기 로직을 구현할 때
b번 세로선에서 a번 가로선을 만났을 때 b + 1번 세로선로 이동시킬 수 있고,
반대로도 저장해 주어야지만 b + 1번 세로선에서 a번 가로선을 만났을 때 b번 세로선으로 이동시켜줄 수 있다.
또한, 사다리의 입력을 저장할 2차원 리스트의 행의 크기가 n이 아닌 n + 2인 것을 볼 수 있는데, 이는 가로선을 추가할 수 있는 위치를 판별하기 쉽게 하기위해 사용하지 않는 임의의 0번 세로선과 n + 1번 세로선을 추가했다고 생각하면 된다.
- 비어있는 가로선의 위치를 저장한다.
blank_h = []
for i in range(1, n):
for j in range(1, h + 1):
if [i, j] in ladders[i - 1] or [i + 1, j] in ladders[i] or [i + 2, j] in ladders[i + 1]:
continue
blank_h.append([i, j])이때도 문제에서 주어진 것과 같이 가로선을 추가할 수 없는 위치가 존재하는데, 이는 추가할 위치에 평행하고 좌우로 인접한 가로선이 존재하는 경우이므로 이 경우를 제외한 가능한 가로선의 위치를 저장해준다.
이는 b번 세로선에서 b + 1번 세로선으로 이동하는 추가 가능한 a번 가로선을 저장한다는 의미와 같다.
- 추가할 가로선의 개수를 정하고, 이 개수에 맞춰 가로선을 추가한다.
ans = -1
for i in range(0 if m % 2 == 0 else 1, (n - 1) * h, 2):
if i <= 3:
cnt = i
tmp = []
dfs(0, 0)
else:
break사다리 타기에대해 생각해 보면 임의의 한 세로선에서 출발하여 같은 세로선으로 출발하기 위해선 사다리에 존재하는 가로선의 총 개수가 짝수여야만 가능하다.
또한 문제에서 주어진 바와 같이 가로선을 3개보다 많이 설치해야 하는 경우에서 정답에서 고려하지 않으므로,
입력으로 주어진 가로선의 개수가 짝수이면 가로선을 0개와 2개를 추가할 수 있고,
입력으로 주어진 가로선의 개수가 홀수이면 가로선을 1개와 3개를 추가할 수 있다.
- 위 3번 단계에서 정한 추가할 가로선의 개수에 따라 가능한 모든 자리에 가로선을 추가한다.
def dfs(start, depth):
global ans
if depth == cnt:
if check():
if ans == -1:
ans = cnt
else:
ans = min(ans, cnt)
return
for i in range(start, len(blank_h)):
tmp.append(blank_h[i])
dfs(i + 1, depth + 1)
tmp.pop()이제 추가할 가로선의 개수까지 정했다면 직접 이전에 blank_h 리스트에 저장했던 가로선을 추가할 수 있는 공간에 개수에 맞춰 가로선을 추가할 차례이다.
이때는 간단한 백트래킹 알고리즘을 사용하였다.
- 가로선을 모두 추가하였다면, 사다리 타기 로직을 실행시켜 모든 세로선이 마지막에 자신과 같은 세로선에 도착하는지 확인한다.
def check():
tmp_ladders = [ladders[i][:] for i in range(n + 1)]
for i in range(len(tmp)):
tmp_ladders[tmp[i][0]].append([tmp[i][0] + 1, tmp[i][1]])
tmp_ladders[tmp[i][0] + 1].append([tmp[i][0], tmp[i][1]])
for i in range(1, n + 1):
tmp_ladders[i].sort(key=lambda x: x[1])
for i in range(1, n + 1):
curr_ladder = i
curr_h = 0
while True:
for j in range(len(tmp_ladders[curr_ladder])):
next, h_pos = tmp_ladders[curr_ladder][j]
if h_pos > curr_h:
curr_ladder = next
curr_h = h_pos
break
else:
break
if curr_ladder == i:
continue
else:
return False
return True이때는 check() 함수를 사용하여 처음 사다리 상태를 그래프 형식으로 입력받았으므로,
각 세로선에서 출발하여 가로선을 만날 경우, 그에 이어진 세로선으로 이동시키며 모든 세로선에서 출발한 세로선과 같은 세로선에 도착하는지 확인하고,
조건에 맞는 사다리 형태가 확인되었다면 True를, 아니면 False를 return하여 정답을 출력한다.
📒 코드
def dfs(start, depth):
global ans
if depth == cnt:
if check():
if ans == -1:
ans = cnt
else:
ans = min(ans, cnt)
return
for i in range(start, len(blank_h)):
tmp.append(blank_h[i])
dfs(i + 1, depth + 1)
tmp.pop()
def check():
tmp_ladders = [ladders[i][:] for i in range(n + 1)]
for i in range(len(tmp)):
tmp_ladders[tmp[i][0]].append([tmp[i][0] + 1, tmp[i][1]])
tmp_ladders[tmp[i][0] + 1].append([tmp[i][0], tmp[i][1]])
for i in range(1, n + 1):
tmp_ladders[i].sort(key=lambda x: x[1])
for i in range(1, n + 1):
curr_ladder = i
curr_h = 0
while True:
for j in range(len(tmp_ladders[curr_ladder])):
next, h_pos = tmp_ladders[curr_ladder][j]
if h_pos > curr_h:
curr_ladder = next
curr_h = h_pos
break
else:
break
if curr_ladder == i:
continue
else:
return False
return True
n, m, h = map(int, input().split())
ladders = [[] for _ in range(n + 2)]
for _ in range(m):
a, b = map(int, input().split())
ladders[b].append([b + 1, a])
ladders[b + 1].append([b, a])
blank_h = []
for i in range(1, n):
for j in range(1, h + 1):
if [i, j] in ladders[i - 1] or [i + 1, j] in ladders[i] or [i + 2, j] in ladders[i + 1]:
continue
blank_h.append([i, j])
ans = -1
for i in range(0 if m % 2 == 0 else 1, (n - 1) * h, 2):
if i <= 3:
cnt = i
tmp = []
dfs(0, 0)
else:
break
print(ans)💭 후기
사다리를 입력받는 단계부터, 추가 가능한 가로선의 자리를 저장하고 마지막엔 직접 사다리 타기 로직을 구현해야 한다는 점에서 굉장히 까다로웠지만 내가 직접 사다리 타기를 구현하고 실행시켜 본다는 점에서 재미있고 뿌듯했던 문제였다.
🔗 문제 출처
https://www.acmicpc.net/problem/15684
