


💡 문제

위쪽 삼각형은 9개의 단위 삼각형이 총 3줄(N=3)로 이루어져 있다. 단위 삼각형은 N=1인 삼각형이다.
이때, 그림에서 서로 다른 부분 삼각형은 총 13개가 있다. (N=1인 삼각형이 9개, N=2인 삼각형이 3개, N=3인 삼각형이 1개)
N = 1인 경우 부분 삼각형은 1개, 2인 경우에는 5개, 3인 경우는 13개, 4인 경우는 27개가 있다.
이때, 단위 삼각형의 값을 삼각형 내부에 쓰여 있는 숫자의 값이라고 하자. 삼각형의 값은 삼각형 안에 있는 단위 삼각형의 값의 합이다.
아래 그림은 가장 큰 값을 갖는 부분 삼각형이다.
삼각형이 주어졌을 때, 가장 큰 값을 갖는 부분 삼각형을 구하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있고, 각 테스트 케이스는 한 줄로 이루어져 있다. 첫 번째 숫자는 줄의 수를 나타내고, 다음 숫자는 단위 삼각형에 적혀있는 값이 위에서 아래, 왼쪽에서 오른쪽 순서대로 주어진다. 마지막 줄에는 0이 주어진다.
줄의 개수는 400을 넘지 않으며, 단위 삼각형에 적혀있는 값의 절댓값은 1000을 넘지 않는다.
출력
각 테스트 케이스에 대해서, 테스트 케이스의 번호와 가장 큰 부분 삼각형의 값을 출력한다.
💭 접근
우선 문제를 풀기 전, 삼각형을 그려보고 문제를 이해해보자.
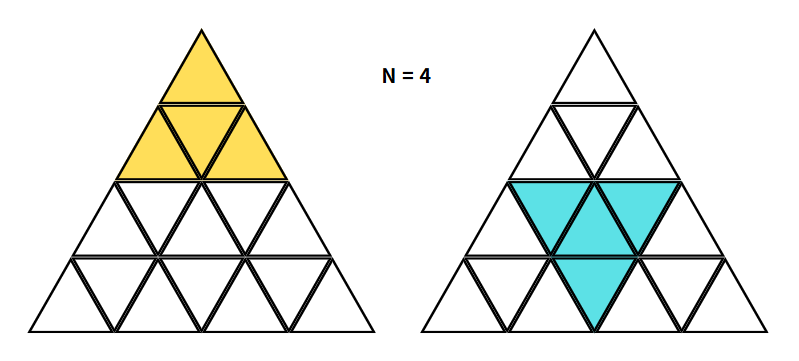
삼각형의 부분 삼각형이라 함은, 위 그림의 주황색 삼각형 영역과 같이 정삼각형과 이를 뒤집은 하늘색 영역의 역삼각형이 그려질 수 있다는 것을 알 수 있다.
또한, 가장 아래줄의 삼각형의 개수는 개가 된다는 것을 알 수 있다.
이를 미루어 보아 먼저 삼각형에 쓰인 값을 저장하기 위한 리스트와 부분 삼각형의 합을 빠르게 구하기 위한 누적합을 저장하기 위한 비어있는 리스트를 생성한다.
tri = [[0 for _ in range(2 * n - 1)] for _ in range(n)]
p_sum = [[0 for _ in range(2 * n)] for _ in range(n)]이후, 삼각형과 누적합을 리스트에 저장할 차례이다.
idx = 0
for i in range(n):
for j in range(2 * i + 1):
tri[i][j] = num[idx]
p_sum[i][j + 1] = tri[i][j] + p_sum[i][j]
idx += 1이렇게 저장을 마치면 다음과 같이 직각 삼각형의 형태로 리스트에 개별 삼각형들의 값이 저장될 것이다.
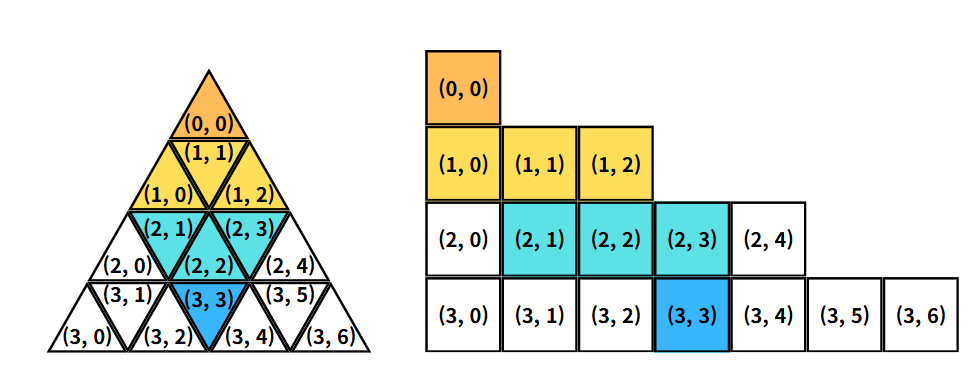
위 그림으로 알 수 있듯이,
정삼각형의 경우 가장 위에 위치하는 삼각형은 짝수 열에 위치하는 것을 볼 수 있고,
역삼각형의 경우 가장 아래에 위치하는 삼각형은 홀수 열에 위치하는 것을 볼 수 있다.
이후 calculate() 함수를 호출하여 정답을 구해주면 된다.
def calculate(i, j):
global ans
tmp = 0
odd = j % 2
r = i
c1, c2 = j, j
while is_valid(r, c1) and is_valid(r, c2):
tmp += get_p_sum(r, c1, c2)
ans = max(ans, tmp)
if odd:
r -= 1
c1 -= 2
else:
r += 1
c2 += 2이때 부분 삼각형의 크기를 구할때도 볼 수 있듯이 odd 변수를 사용하여 기준이 되는 삼각형의 열이 짝수, 홀수인지에 따라 더할 삼각형의 좌표값도 다르게 설정해주는 것을 볼 수 있다.
📒 코드
def get_p_sum(r, c1, c2):
return p_sum[r][c2 + 1] - p_sum[r][c1]
def is_valid(r, c):
return 0 <= r < n and 0 <= c < 2 * r + 1
def calculate(i, j):
global ans
tmp = 0
odd = j % 2
r = i
c1, c2 = j, j
while is_valid(r, c1) and is_valid(r, c2):
tmp += get_p_sum(r, c1, c2)
ans = max(ans, tmp)
if odd:
r -= 1
c1 -= 2
else:
r += 1
c2 += 2
case_num = 1
while True:
tri_info = list(map(int, input().split()))
n = tri_info[0]
if n == 0:
break
num = tri_info[1:]
tri = [[0 for _ in range(2 * n - 1)] for _ in range(n)]
p_sum = [[0 for _ in range(2 * n)] for _ in range(n)]
idx = 0
for i in range(n):
for j in range(2 * i + 1):
tri[i][j] = num[idx]
p_sum[i][j + 1] = tri[i][j] + p_sum[i][j]
idx += 1
ans = -float('inf')
for i in range(n):
for j in range(2 * i + 1):
calculate(i, j)
print(f'{case_num}. {ans}')
case_num += 1💭 후기
정삼각형과 역삼각형의 경우를 따지고 이들의 합을 구하는 방법을 떠올리는 것이 굉장히 까다로웠다.
🔗 문제 출처
https://www.acmicpc.net/problem/4902
