


💡 문제
BOJ에서 정답이 여러가지인 경우에는 스페셜 저지를 사용한다. 스페셜 저지는 유저가 출력한 답을 검증하는 코드를 통해서 정답 유무를 결정하는 방식이다. 오늘은 스페셜 저지 코드를 하나 만들어보려고 한다.
정점의 개수가 N이고, 정점에 1부터 N까지 번호가 매겨져있는 양방향 그래프가 있을 때, BFS 알고리즘은 다음과 같은 형태로 이루어져 있다.
- 큐에 시작 정점을 넣는다. 이 문제에서 시작 정점은 1이다. 1을 방문했다고 처리한다.
- 큐가 비어 있지 않은 동안 다음을 반복한다.
- 큐에 들어있는 첫 정점을 큐에서 꺼낸다. 이 정점을 x라고 하자.
- x와 연결되어 있으면, 아직 방문하지 않은 정점 y를 모두 큐에 넣는다. 모든 y를 방문했다고 처리한다.
2-2 단계에서 방문하지 않은 정점을 방문하는 순서는 중요하지 않다. 따라서, BFS의 결과는 여러가지가 나올 수 있다.
트리가 주어졌을 때, 올바른 BFS 방문 순서인지 구해보자.
입력
첫째 줄에 정점의 수 N(2 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N-1개의 줄에는 트리의 간선 정보가 주어진다. 마지막 줄에는 BFS 방문 순서가 주어진다. BFS 방문 순서는 항상 N개의 정수로 이루어져 있으며, 1부터 N까지 자연수가 한 번씩 등장한다.
출력
입력으로 주어진 BFS 방문 순서가 올바른 순서면 1, 아니면 0을 출력한다.
💭 접근
먼저 예제를 통해 문제를 살펴보자.
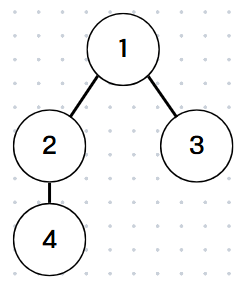
예제 1에서 주어진 그래프를 그려보면 이와 같이 나타낼 수 있고,
1부터 탐색을 시작하면 나올수 있는 탐색 순서는 (1 2 3 4), (1 3 2 4)로 볼 수 있다.
이해를 위해 더 복잡한 그래프를 예로 들어보자,
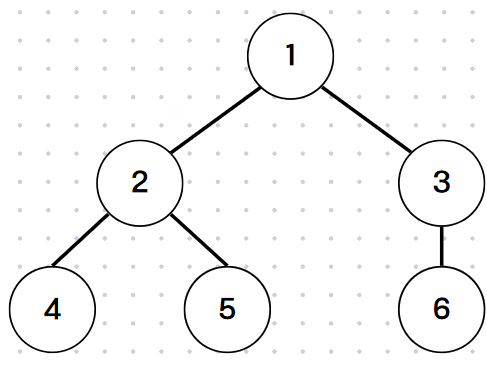
위와 같은 그래프를 1부터 탐색했을 때 올바른 탐색 순서는
(1 2 3 4 5 6), (1 2 3 5 4 6), (1 3 2 6 4 5), (1 3 2 6 5 4)
가 될 수 있는데 이를 보면 부모-자식 관계에 따라 순서가 정해지는 것을 볼 수 있다.
빨간색은 2와 2의 자식 노드, 파란색은 3과 3의 자식노드
(1 {2 3} {4 5 6})
(1 {2 3} {5 4 6})
(1 {3 2} {6 4 5})
(1 {3 2} {6 5 4})
이처럼 중괄호로 묶인 형제 노드들의 자식 노드들은 자신들의 순서와는 상관 없지만 그 위 부모 노드의 순서에 영향을 받는다는 것을 알 수 있다.
따라서, 먼저 각 노드들의 부모-자식 관계를 찾은 뒤, 이들을 집합으로 묶어 비교를 해주면 입력으로 주어진 순서가 올바른 순서인지 알 수 있다.
코드와 함께 살펴보자.
- 우선, Python의 defaultdict 자료형을 사용하여 부모-자식 간의 관계를 저장해준다. 이때 defaultdict란 Pandas의 DataFrame과 비슷한데, 데이터를 저장하는 방식은 Python의 dictionary와 비슷하지만, 미리 키값을 지정하지 않고 저장을 하여도 그 키 값에 따른 데이터를 dictionary의 형태로 저장해준다.
예제 1번을 예시로 bfs() 함수 종료후 children을 출력해보면,
defaultdict(<class 'list'>, {1: [2, 3], 2: [4]})이와같이 출력되는 것을 확인할 수 있다.
def bfs():
q = deque()
q.append(1) # BFS 1부터 시작
visited[1] = True
while q:
x = q.popleft()
for next in graph[x]:
if not visited[next]:
visited[next] = True
children[x].append(next) # 딕셔너리에 부모-자식 관계 저장
q.append(next)- 부모-자식 관계를 저장하였으면, 이를 이용하여 bfs처럼 입력받은 순서가 참인지 검사한다. 이때, 각 부모 노드의 자식 수만큼 입력받은 순서를 슬라이싱하여 집합(set)으로 b에 저장한 뒤, children에 저장되어 있는 부모 노드의 자식 또한 집합(set)으로 저장하여 비교해준다. 이때 슬라이싱 작업을 할 때 주의해야 할 것이 있는데, 집합으로 집합 속에 있는 자식 노드들을 한번에 비교하는 것이기에 그 자식 수 만큼 더해주며 슬라이싱 해야한다.
b = ans[idx:idx + len(a)]
q = deque()
q.append(1) # BFS 1부터 시작
idx = 1 # ans[0] 헀으니까 1부터 시작
while q:
x = q.popleft()
a = set(children[x]) # a에 x의 자식노드 저장
b = ans[idx:idx + len(a)] # 그 depth만큼 슬라이싱 -> x의 자식노드 자르기
q.extend(b) # 다음 탐색할 노드로 저장
b = set(b) # 비교 위해서 set으로 변환
idx += len(a) # 다음 자식노드 탐색하기 위해 idx 늘려주기
if a != b: # 둘의 집합이 다르다면
print(0)
break
else:
print(1)📒 코드
import sys
from collections import deque, defaultdict
# input = sys.stdin.readline
def bfs():
q = deque()
q.append(1) # BFS 1부터 시작
visited[1] = True
while q:
x = q.popleft()
for next in graph[x]:
if not visited[next]:
visited[next] = True
children[x].append(next) # 딕셔너리에 부모-자식 관계 저장
q.append(next)
n = int(input())
graph = [[] for _ in range(n + 1)]
visited = [False for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
ans = list(map(int, input().split()))
children = defaultdict(list)
bfs()
# print(children) # defaultdict(<class 'list'>, {1: [2, 3], 2: [4]})
if ans[0] != 1:
print(0)
else:
q = deque()
q.append(1) # 1 = ans[0]
idx = 1 # ans[0] 헀으니까 1부터 시작
while q:
x = q.popleft()
a = set(children[x]) # a에 x의 자식노드 저장
b = ans[idx:idx + len(a)] # 그 depth만큼 슬라이싱 -> x의 자식노드 자르기
q.extend(b) # 다음 탐색할 노드로 저장
b = set(b) # 비교 위해서 set으로 변환
idx += len(a) # 다음 자식노드 탐색하기 위해 idx 늘려주기
if a != b: # 둘의 집합이 다르다면
print(0)
break
else:
print(1)💭 후기
BFS를 사용하여 탐색만 할 줄 알았지 탐색이 완료된 순서가 참인지 찾아내는 것은 매우 까다로웠다. 또한 Python의 defaultdict 자료형 또한 알게 되었다.
🔗 문제 출처
https://www.acmicpc.net/problem/16940
