


💡 문제
BOJ에서 정답이 여러가지인 경우에는 스페셜 저지를 사용한다. 스페셜 저지는 유저가 출력한 답을 검증하는 코드를 통해서 정답 유무를 결정하는 방식이다. 오늘은 스페셜 저지 코드를 하나 만들어보려고 한다.
정점의 개수가 N이고, 정점에 1부터 N까지 번호가 매겨져있는 양방향 그래프가 있을 때, DFS 알고리즘은 다음과 같은 형태로 이루어져 있다.
void dfs(int x) {
if (check[x] == true) {
return;
}
check[x] = true;
// x를 방문
for (int y : x와 인접한 정점) {
if (check[y] == false) {
dfs(y);
}
}
}이 문제에서 시작 정점은 1이기 때문에 가장 처음에 호출하는 함수는 dfs(1)이다. DFS 방문 순서는 dfs함수에서 // x를 방문 이라고 적힌 곳에 도착한 정점 번호를 순서대로 나열한 것이다.
트리가 주어졌을 때, 올바른 DFS 방문 순서인지 구해보자.
입력
첫째 줄에 정점의 수 N(2 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N-1개의 줄에는 트리의 간선 정보가 주어진다. 마지막 줄에는 DFS 방문 순서가 주어진다. DFS 방문 순서는 항상 N개의 정수로 이루어져 있으며, 1부터 N까지 자연수가 한 번씩 등장한다.
출력
입력으로 주어진 DFS 방문 순서가 올바른 순서면 1, 아니면 0을 출력한다.
💭 접근
먼저 예제를 통해 문제를 살펴보자
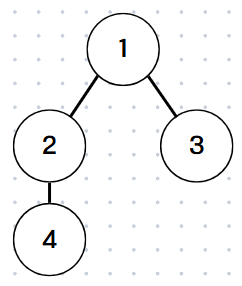
예제 1에서 주어진 그래프를 그려보면 이와 같이 나타낼 수 있고,
1부터 탐색을 시작하면 나올 수 있는 탐색 순서는 (1 2 4 3), (1 3 2 4)가 될 수 있다.
이해를 위해 더 복잡한 그래프를 예로 들어보자.
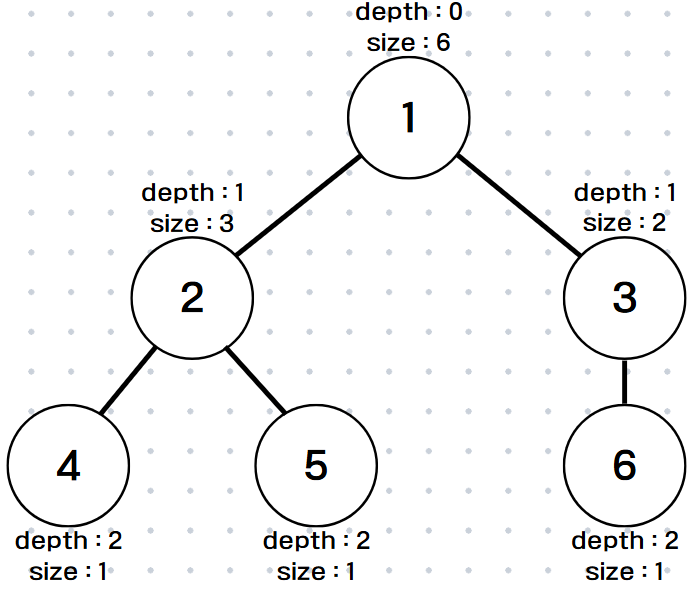
위와 같은 그래프를 1부터 탐색했을 때 올바른 탐색 순서는
(1 2 4 5 3 6), (1 2 5 4 3 6), (1 3 6 2 4 5), (1 3 6 2 5 4)
가 될 수 있는데 이들은 부모-형제-자식 노드의 관계에 따라 순서가 정해지는 것을 볼 수 있다.
이 중 하나를 예로 들어보자.
ans = 1 2 4 5 3 6
1 2 4 5 3 6 -> 1 + size[1] -> 1 + 6 = 7 -> continue (전체 그래프의 크기보다 큼)
1 2 4 5 3 6 -> 2 + size[2] -> 2 + 3 = 5 -> ans[5] = 3 -> 2와 3의 depth가 같음
1 2 4 5 3 6 -> 3 + size[4] -> 3 + 1 = 4 -> ans[4] = 5 -> 4와 5의 depth가 같음
1 2 4 5 3 6 -> 4 + size[5] -> 4 + 1 = 5 -> ans[5] = 3 -> 5보다 3의 depth가 작음
1 2 4 5 3 6 -> 5 + size[3] -> 5 + 2 = 7 -> continue (전체 그래프의 크기보다 큼)
1 2 4 5 3 6 -> 6 + size[6] -> 6 + 1 = 7 -> continue (전체 그래프의 크기보다 큼)
이처럼 입력으로 주어진 방문 순서가 참인지 판별하려면 주어진 입력을 순서대로 반복하며 자신의 위치에서 자신의 size를 더한 위치에 있는 노드가 자신보다 depth가 작거나 같아야하며, 크면 거짓이다.
- 우선, 1부터 DFS를 호출하여 각 노드들의 depth와 size를 저장한다.
def dfs(start, depth):
if visited[start]:
return 0
visited[start] = True
size = 1 # 최소 크기는 1 -> 자기 자신
node_depth[start] = depth # 각 노드의 depth 저장
for next in graph[start]: # 각 노드를 시작으로 하는 트리의 크기 저장
if not visited[next]:
size += dfs(next, depth + 1)
node_size[start] = size
return size- 이후, 입력으로 주어진 방문 순서를 앞에서부터 차례대로 반복하며 (각 노드의 입력에서의 위치 + 각 노드의 size) 위치에 있는 노드와 depth를 비교하여 현재 노드보다 뒤에 있는 노드의 depth가 크다면 break
if ans[1] != 1:
print(0)
else:
dfs(1, 0)
for i in range(1, n):
# 크기가 1이면 가장 마지막에 있는 노드이고, i + node_size[ans[i]]가 n보다 크거나 같아지면 IndexError 발생!
# ex) 1 - 2 - 3 - 4 -> 1 + node_size[ans[1]] -> 1 + 4 = 5 (IndexError)
if i + node_size[ans[i]] > n:
continue
if node_depth[ans[i]] < node_depth[ans[i + node_size[ans[i]]]]:
print(0)
break
else:
print(1)📒 코드
import sys
input = sys.stdin.readline
def dfs(start, depth):
if visited[start]:
return 0
visited[start] = True
size = 1 # 최소 크기는 1 -> 자기 자신
node_depth[start] = depth # 각 노드의 depth 저장
for next in graph[start]: # 각 노드를 시작으로 하는 트리의 크기 저장
if not visited[next]:
size += dfs(next, depth + 1)
node_size[start] = size
return size
n = int(input())
graph = [[] for _ in range(n + 1)]
visited = [False for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
ans = [0] + list(map(int, input().split()))
node_depth = [0 for _ in range(n + 1)]
node_size = [0 for _ in range(n + 1)]
if ans[1] != 1:
print(0)
else:
dfs(1, 0)
for i in range(1, n):
# 크기가 1이면 가장 마지막에 있는 노드이고, i + node_size[ans[i]]가 n보다 크거나 같아지면 IndexError 발생!
# ex) 1 - 2 - 3 - 4 -> 1 + node_size[ans[1]] -> 1 + 4 = 5 (IndexError)
if i + node_size[ans[i]] > n:
continue
if node_depth[ans[i]] < node_depth[ans[i + node_size[ans[i]]]]:
print(0)
break
else:
print(1)💭 후기
16940번 BFS 스페셜 저지 문제와 접근 방식이 비슷해서 풀이를 금방 떠올렸던 것 같다.
🔗 문제 출처
https://www.acmicpc.net/problem/16964
