


💡 문제
N개의 수로 된 수열 A[1], A[2], …, A[N] 이 있다. 이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i+1] + … + A[j-1] + A[j]가 M이 되는 경우의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)이 주어진다. 다음 줄에는 A[1], A[2], …, A[N]이 공백으로 분리되어 주어진다. 각각의 A[x]는 30,000을 넘지 않는 자연수이다.
출력
첫째 줄에 경우의 수를 출력한다.
💭 접근
이 문제는 기본적인 투포인터 알고리즘을 사용하는 문제이다. 예제 2번을 예로 들어 살펴보자.
ex) 예제 2번: n = 10, m = 5, a = [1, 2, 3, 4, 2, 5, 3, 1, 1, 2]
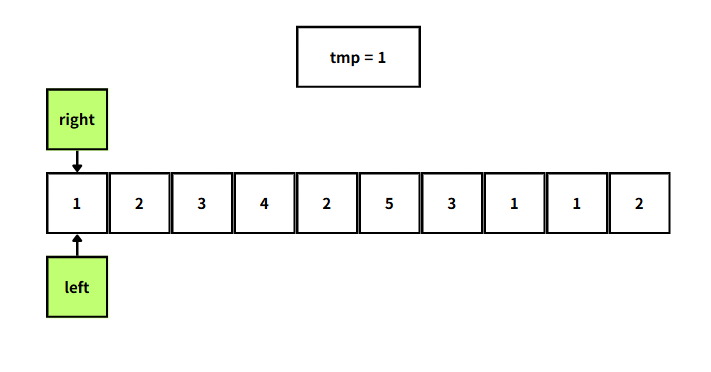
초기에는 이러한 상태로 tmp가 1로 5보다 작으므로 right += 1을 해주고 해당 인덱스의 원소를 더해준다.
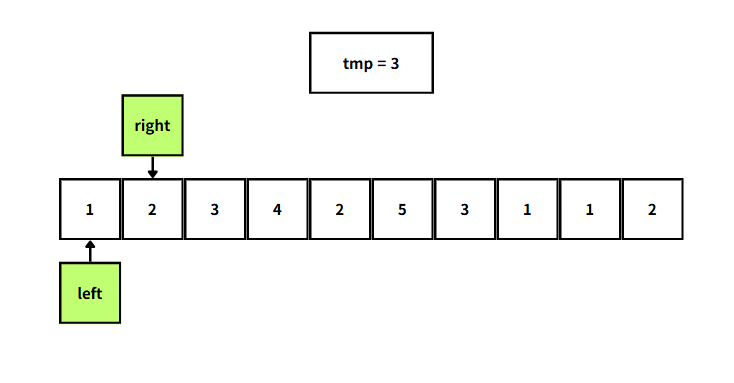
여전히 tmp가 3으로 5보다 작으므로 right를 한칸 더 옮겨준다.
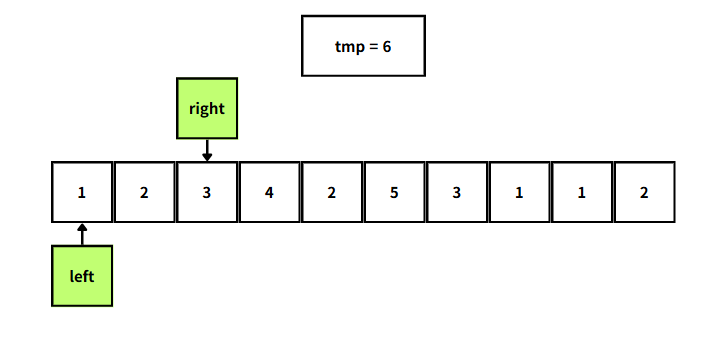
이렇게 되면 tmp가 6으로 5보다 크므로 현재 left가 가리키고 있는 수를 뺀 뒤, left += 1을 해준다.
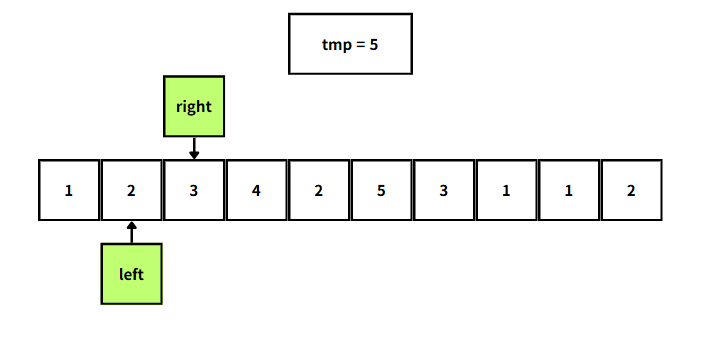
그러면 tmp는 5가 되므로 ans에 1을 더해주고 다시 2를 뺀 뒤, left를 한칸 더 이동시켜준다.
따라서 left와 right를 이동시키면서 tmp가 5가 될수 있는 경우는 다음과 같다.
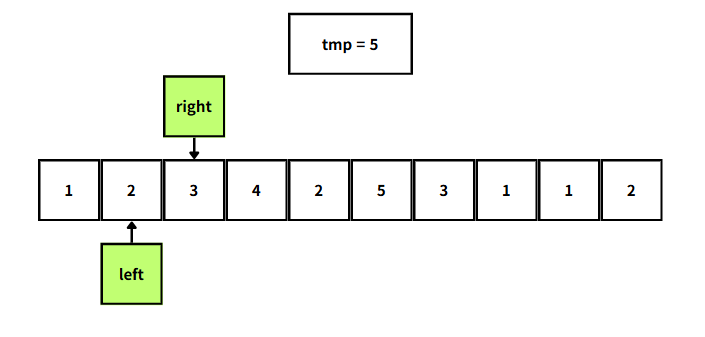
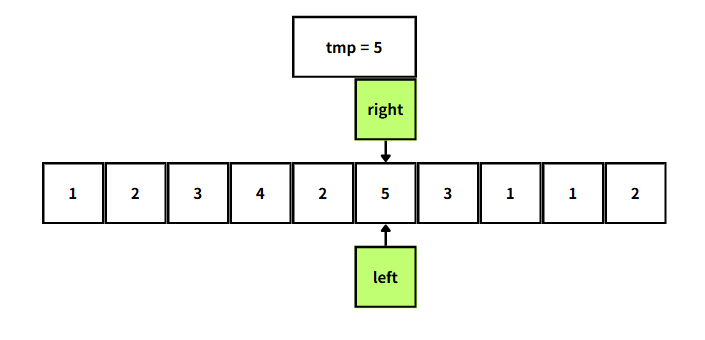
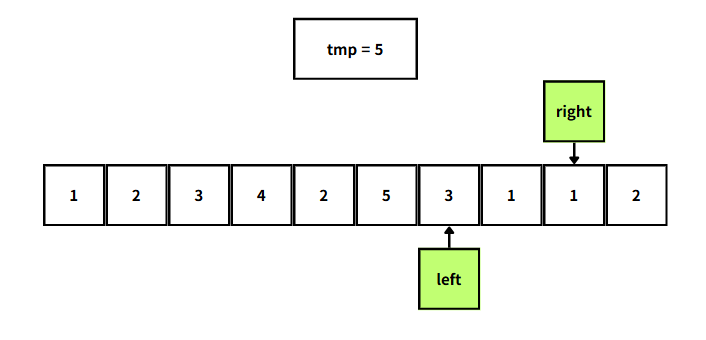
앞서 살펴본 내용을 정리해보면, left와 right를 부분배열의 범위로 보고,
tmp가 목표 숫자보다 크거나 같으면 left를 이동시켜 부분배열의 크기를 줄이고,
tmp가 목표 숫자보다 작으면 right를 이동시켜 부분배열의 크기를 늘려 tmp 값을 조절해나가면 된다.
이렇게 하면 각각의 부분배열의 합을 2중 for문이 아닌 하나의 반복문으로 구현할 수 있어 시간복잡도 측면에서 매우 효율적이다.
그러나 이러한 단순한 로직은 현재 문제에서 (각각의 원소는 "자연수"이다.)라는 조건을 주었기에 가능하고, 만약 음수가 포함된 경우는 이러한 방법으로 풀 수 없다.
📒 코드
n, m = map(int, input().split())
a = list(map(int, input().split()))
tmp = a[0]
left = 0
right = 0
ans = 0
while True:
if tmp < m:
right += 1
if right >= n:
break
tmp += a[right]
else:
if tmp == m:
ans += 1
tmp -= a[left]
left += 1
print(ans)💭 후기
투포인터 알고리즘을 사용하는 간단한 문제였다.
🔗 문제 출처
https://www.acmicpc.net/problem/2003
