


💡 문제
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.
이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북으로 육지가 붙어있는 덩어리를 말한다. 다음은 세 개의 섬으로 이루어진 나라의 지도이다.
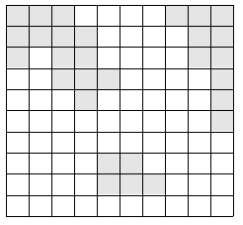
위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다.
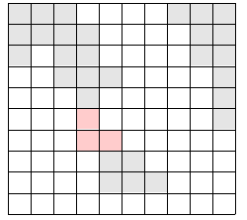
물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).
지도가 주어질 때, 가장 짧은 다리 하나를 놓아 두 대륙을 연결하는 방법을 찾으시오.
입력
첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다. 항상 두 개 이상의 섬이 있는 데이터만 입력으로 주어진다.
출력
첫째 줄에 가장 짧은 다리의 길이를 출력한다.
💭 접근
우선 이 문제에선 2가지의 BFS 함수를 사용하여 해결하였다. 각각의 섬을 구분짓는 numbering_island() 함수와 각각의 섬을 잇는 다리를 건설하는 building_bridge() 함수이다. 함수를 하나씩 살펴보자.
1. numbering_island()
def numbering_island(x, y, num):
q = deque()
q.append((x, y))
while q:
x, y = q.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < n and graph[nx][ny] == 1: # 1-1 바다 말고 섬일때만
graph[nx][ny] = num
q.append((nx, ny))먼저, 각기 다른 섬을 잇는 다리를 건설하려면 먼저 섬을 구분지을 필요가 있다. 그래서 입력으로 주어진 graph에서 모든 원소를 탐색하며 1이면 섬이므로 그때 하나의 섬에대해 -1, -2, -3, ...과 같이 음수로 넘버링을 해주었다. 이를 그림으로 나타내면,
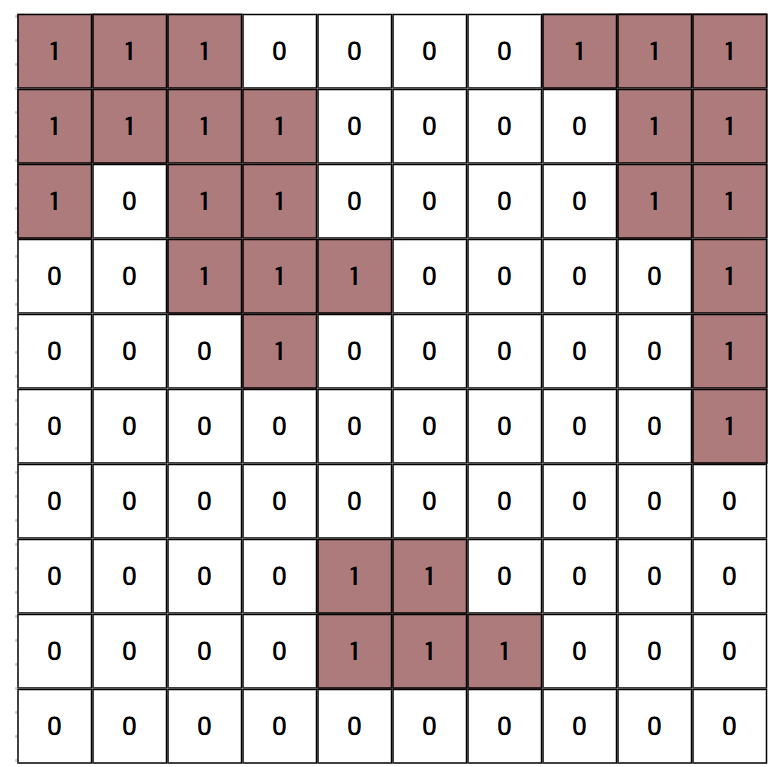
이러한 graph에서 numbering_island() 함수를 적용하면,
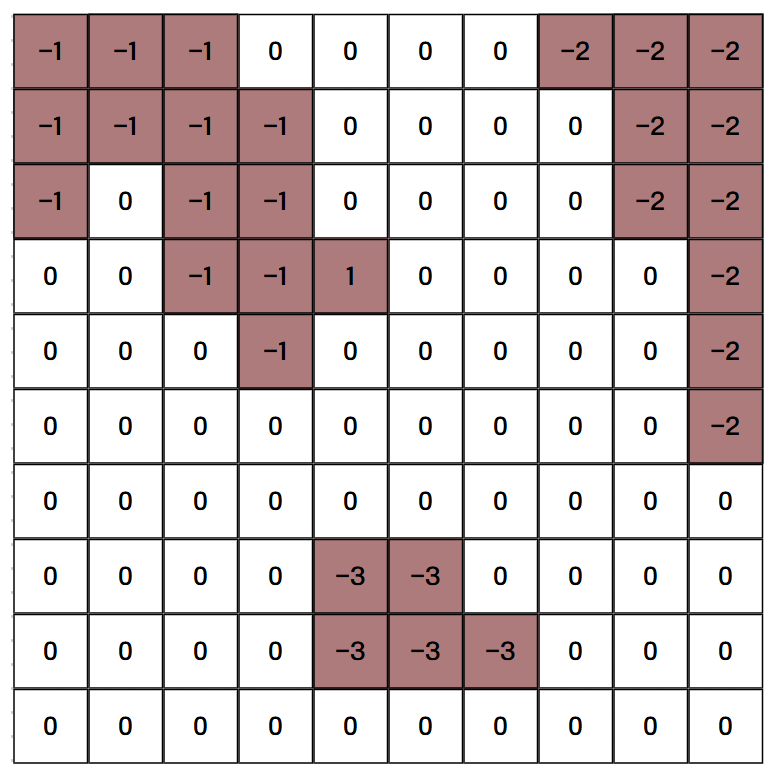
위 그림과 같이 각기 다른 섬마다 번호를 매겨준다. 이제 섬을 구분지었으니 다리를 건설할 차례이다.
2. building_bridge()
def building_bridge(x, y):
global ans
q = deque()
q.append((x, y))
break_flag = False
while q:
x, y = q.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < n:
if tmp[nx][ny] == 0: # 2-1. 0일때만 (바다 일때만)
tmp[nx][ny] = tmp[x][y] + 1
q.append((nx, ny))
# 2-2. 만약 음수를 만났는데 (섬인데) 시작 섬번호가 아니면 break
elif tmp[nx][ny] < 0 and tmp[nx][ny] != origin_num:
ans = min(ans, tmp[x][y])
break_flag = True
break
if break_flag:
break모든 섬의 가장자리에서 출발하여, 바다일 때만 다리를 지으며 나아간다. 이때 종료 조건으로는, 바다가 아닐 때 (tmp[nx][ny] < 0), 그리고 모든 섬은 음수이므로 음수면서 원래 섬의 번호와 다를 때 (tmp[nx][ny] != origin_num) 다른 섬에 도달한 것으로 판단하고 함수를 종료 후, 다리의 최소길이를 갱신한다.
📒 코드
import sys
from collections import deque
def numbering_island(x, y, num):
q = deque()
q.append((x, y))
while q:
x, y = q.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < n and graph[nx][ny] == 1: # 1-1 바다 말고 섬일때만
graph[nx][ny] = num
q.append((nx, ny))
def building_bridge(x, y):
global ans
q = deque()
q.append((x, y))
break_flag = False
while q:
x, y = q.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < n:
if tmp[nx][ny] == 0: # 2-1. 0일때만 (바다 일때만)
tmp[nx][ny] = tmp[x][y] + 1
q.append((nx, ny))
# 2-2. 만약 음수를 만났는데 (섬인데) 시작 섬번호가 아니면 break
elif tmp[nx][ny] < 0 and tmp[nx][ny] != origin_num:
ans = min(ans, tmp[x][y])
break_flag = True
break
if break_flag:
break
n = int(input())
graph = [list(map(int, input().split())) for _ in range(n)]
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
num = -1
for i in range(n): # 모든 섬에 대해서 넘버링
for j in range(n):
if graph[i][j] == 1:
graph[i][j] = num
numbering_island(i, j, num)
# 섬 하나 통째로 넘버링 했으면 다음 섬 번호 -- 해주기
num -= 1
ans = sys.maxsize
for i in range(n):
for j in range(n):
if graph[i][j] < 0: # 섬에 대해서만 실행 (섬 번호는 음수니까)
# 현재 섬 번호 저장 (다른 섬이랑 안헷갈리게 <- 종료조건이므로)
origin_num = graph[i][j]
tmp = [graph[i][:] for i in range(n)] # 다리 그렸던던거 초기화
tmp[i][j] = 0
building_bridge(i, j)
print(ans)💭 후기
어떻게하면 어떤 섬에서 다른 섬까지 잇는 다리를 건설할 수 있을까를 충분히 구상 후 문제를 해결하였다.
🔗 문제 출처
https://www.acmicpc.net/problem/2146
