


💡 문제
스도쿠가 세계적으로 유행이 된 이후에, 비슷한 퍼즐이 매우 많이 나왔다. 게임 매거진 2009년 7월호에는 스도쿠와 도미노를 혼합한 게임인 스도미노쿠가 소개되었다.
이 퍼즐은 스도쿠 규칙을 따른다. 스도쿠는 9×9 크기의 그리드를 1부터 9까지 숫자를 이용해서 채워야 한다. 스도쿠는 다음과 같은 조건을 만족하게 숫자를 채워야 한다.
- 각 행에는 1부터 9까지 숫자가 하나씩 있어야 한다.
- 각 열에는 1부터 9까지 숫자가 하나씩 있어야 한다.
- 3×3크기의 정사각형에는 1부터 9가지 숫자가 하나씩 있어야 한다.
스도미노쿠의 그리드에는 1부터 9까지 숫자가 쓰여져 있고, 나머지 72칸은 도미노 타일 36개로 채워야 한다. 도미노 타일은 1부터 9까지 서로 다른 숫자의 가능한 쌍이 모두 포함되어 있다. (1+2, 1+3, 1+4, 1+5, 1+6, 1+7, 1+8, 1+9, 2+3, 2+4, 2+5, ...) 1+2와 2+1은 같은 타일이기 때문에, 따로 구분하지 않는다. 도미노 타일은 회전 시킬 수 있다. 또, 3×3 크기의 정사각형의 경계에 걸쳐서 놓여질 수도 있다.
왼쪽 그림은 퍼즐의 초기 상태를 나타내고, 오른쪽은 퍼즐을 푼 상태이다.
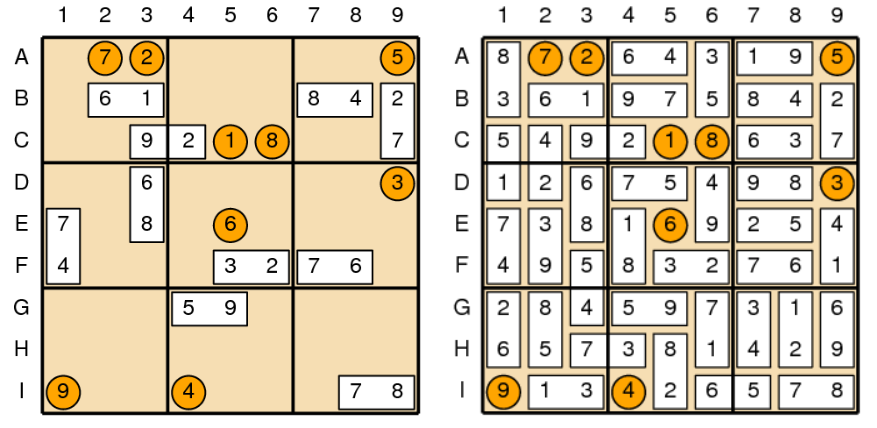
스도미노쿠의 퍼즐의 초기 상태가 주어졌을 때, 퍼즐을 푸는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 채워져 있는 도미노의 개수 N이 주어진다. (10 ≤ N ≤ 35) 다음 N개 줄에는 도미노 하나를 나타내는 U LU V LV가 주어진다. U는 도미노에 쓰여 있는 한 숫자이고, LU는 길이가 2인 문자열로 U의 위치를 나타낸다. V와 LV는 도미노에 쓰여 있는 다른 숫자를 나타낸다. 도미노의 위치는 문제에 나와있는 그림을 참고한다. 입력으로 주어지는 도미노의 각 숫자 위치는 항상 인접해 있다.
N개의 도미노의 정보가 주어진 다음 줄에는 채워져 있는 숫자의 위치가 1부터 9까지 차례대로 주어진다. 위치는 도미노의 위치를 나타낸 방법과 같은 방법으로 주어진다.
모든 도미노와 숫자가 겹치는 경우는 없다.
입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 퍼즐에 대해서, 스도쿠를 푼 결과를 출력한다. 항상 답이 유일한 경우만 입력으로 주어진다.
💭 접근
처음 이 문제를 봤을 땐, 2x1 도미노를 문제에서 주어진 것처럼 하나의 블럭으로 간주하고 2580번 스도쿠 문제와 비슷하게 해결하려 했지만 실패했고, 다른 풀이에서 힌트를 얻은 결과, 2x1 도미노를 한번에 놓는 것이 아닌, 1x1 블럭 하나로 간주하고 놓는 방법을 알게 되었다. 우선 이 문제를 해결하기 위해 많은 함수가 필요한데, 이 함수 먼저 알아보자.
convert: 문자열 좌표를 숫자 좌표로 변환해주는 함수def convert(s): return(ord(s[0]) - ord('A'), ord(s[1]) - ord('1'))put_domino: 도미노를 스도쿠보드 위에 올리는 함수def put_domino(x, y, num, put): row[x][num] = put col[y][num] = put block[get_block_index(x, y)][num] = putget_block_index: 3x3 블럭의 번호를 return 해주는 함수def get_block_index(x, y): return (x//3) * 3 + (y//3)check_range: 도미노가 스도쿠보드를 벗어나지 않는지 확인하는 함수def check_range(x, y): return 0 <= x < 9 and 0 <= y < 9can: 도미노를 스도쿠보드 위에 놓았을 때 스도쿠 규칙을 만족하는지 판단하는 함수def can(x, y, num): return not row[x][num] and not col[y][num] and not block[get_block_index(x, y)][num]
이러한 부수적인 함수들이 존재하고, 마지막으로 DFS 함수를 알아보자.
우선 종료조건이다.
if depth == 81:
for i in range(9):
print(*sudoku[i], sep='')
print()
return True이처럼 보드에 모든 블럭이 놓아진 상태라면 (depth는 보드에 존재하는 블럭의 개수) dfs를 종료하고 완성된 스도쿠보드를 출력한다.
여기서 depth는 스도쿠보드를 탐색하기 위한 x, y좌표를 구하는 데에도 사용된다.
x = depth // 9
y = depth % 9좌표를 구한 후, 백트래킹 기법을 이용하여 조건을 만족하도록 스도쿠보드를 채워나가면 된다.
if sudoku[x][y] != 0: # 이미 도미노가 놓아져 있다면
return dfs(depth + 1)
else: # 반칸인 경우
for k in range(2): # 세로도미노 가로도미노 둘다 확인
nx, ny = x + dx[k], y + dy[k]
if not check_range(nx, ny): # 도미노가 보드 밖으로 나가는지 확인
continue
if sudoku[nx][ny] != 0: # 도미노의 기준의 +1에도 도미노가 없는지 확인
continue
for i in range(1, 10): # 9C2 조합 뽑기
for j in range(1, 10):
if i == j: # 같은 숫자가 쓰여져 있는 도미노는 없으므로
continue
if domino[i][j]: # 이미 사용된 도미노라면 continue
continue
if can(x, y, i) and can(nx, ny, j): # x, y에 도미노를 놓을 수 있다면
put_domino(x, y, i, True) # 여기부턴 백트래킹
put_domino(nx, ny, j, True)
domino[i][j] = True
domino[j][i] = True
sudoku[x][y] = i
sudoku[nx][ny] = j
if dfs(depth + 1):
return True
put_domino(x, y, i, False)
put_domino(nx, ny, j, False)
domino[i][j] = False
domino[j][i] = False
sudoku[x][y] = 0
sudoku[nx][ny] = 0먼저 비어있는 칸에서 check_range 함수를 호출하여 도미노를 놓았을 때 가로 도미노, 세로 도미노에 대해 스도쿠보드를 벗어나지 않는지 확인한다.
도미노가 스도쿠보드를 벗어나지 않는 것이 확인되었다면 도미노를 놓았을 때 다른 수와 겹치지 않는지 확인한다.
이후 위 두 조건이 만족되었다면 조합을 만들면서 이 조합이 이미 사용된 도미노인지 확인한다.
사용되지 않은 도미노인 것이 확인이 되었다면, can 함수를 호출하여 이 도미노를 놓았을 때 스도쿠 규칙에 위배하지 않는지 확인하고, 백트래킹 기법을 이용하여 스도쿠보드를 채워나가면 된다.
📒 코드
import sys
input = sys.stdin.readline
def dfs(depth):
if depth == 81:
for i in range(9):
print(*sudoku[i], sep='')
print()
return True
# 시간을 줄이기 위해 x, y를 depth로 계산 (0,0) ~ (9,9)
x = depth // 9
y = depth % 9
if sudoku[x][y] != 0: # 이미 도미노가 놓아져 있다면
return dfs(depth + 1)
else: # 반칸인 경우
for k in range(2): # 세로도미노 가로도미노 둘다 확인
nx, ny = x + dx[k], y + dy[k]
if not check_range(nx, ny): # 도미노가 보드 밖으로 나가는지 확인
continue
if sudoku[nx][ny] != 0: # 도미노의 기준의 +1에도 도미노가 없는지 확인
continue
for i in range(1, 10): # 9C2 조합 뽑기
for j in range(1, 10):
if i == j: # 같은 숫자가 쓰여져 있는 도미노는 없으므로
continue
if domino[i][j]: # 이미 사용된 도미노라면 continue
continue
if can(x, y, i) and can(nx, ny, j): # x, y에 도미노를 놓을 수 있다면
put_domino(x, y, i, True) # 여기부턴 백트래킹
put_domino(nx, ny, j, True)
domino[i][j] = True
domino[j][i] = True
sudoku[x][y] = i
sudoku[nx][ny] = j
if dfs(depth + 1):
return True
put_domino(x, y, i, False)
put_domino(nx, ny, j, False)
domino[i][j] = False
domino[j][i] = False
sudoku[x][y] = 0
sudoku[nx][ny] = 0
return False
def convert(s): # 문자열 좌표 숫자 좌표로 변환해주는 함수
return(ord(s[0]) - ord('A'), ord(s[1]) - ord('1'))
def put_domino(x, y, num, put): # 도미노를 스도쿠보드 위에 올리는 함수
row[x][num] = put
col[y][num] = put
block[get_block_index(x, y)][num] = put
def get_block_index(x, y): # 3x3 블럭의 번호 return
return (x//3) * 3 + (y//3)
def check_range(x, y): # 0~8까지인 이유 : nx, ny가 x, y 기준으로 +1씩 이기 때문
return 0 <= x < 9 and 0 <= y < 9
def can(x, y, num): # 도미노를 스도쿠보드 위에 놓았을 때 스도쿠 규칙을 만족하는지 판단하는 함수
return not row[x][num] and not col[y][num] and not block[get_block_index(x, y)][num]
cnt = 1
while True:
row = [[False for _ in range(10)] for _ in range(10)]
col = [[False for _ in range(10)] for _ in range(10)]
block = [[False for _ in range(10)] for _ in range(10)]
domino = [[False for _ in range(10)] for _ in range(10)]
sudoku = [[0 for _ in range(9)] for _ in range(9)]
n = int(input())
if n == 0:
break
for i in range(n):
n1, s1, n2, s2 = input().split()
n1 = int(n1)
n2 = int(n2)
x1, y1 = convert(s1)
x2, y2 = convert(s2)
sudoku[x1][y1] = n1
sudoku[x2][y2] = n2
domino[n1][n2] = True
domino[n2][n1] = True
put_domino(x1, y1, n1, True)
put_domino(x2, y2, n2, True)
single_block = list(input().split())
for i in range(1, 10):
s = single_block[i - 1]
x, y = convert(s)
sudoku[x][y] = i
put_domino(x, y, i, True)
print(f'Puzzle {cnt}')
dx = [0, 1]
dy = [1, 0]
dfs(0)
cnt += 1💭 후기
2580번 스도쿠 문제와 비슷해보여 쉽게 생각했지만 생각보다 많이 어려워 시간을 많이 들인 문제였다. 계속 반복적으로 복습해야겠다.
🔗 문제 출처
https://www.acmicpc.net/problem/4574
