⚡ 자바스크립트로 보는 알고리즘 Ⅱ
📌 너비 우선 탐색(BFS)
🔷 그래프 탐색 알고리즘으로 같은 깊이에 해당하는 정점부터 탐색하는 알고리즘
- Queue를 이용하여 구현할 수 있다.
- 시작 지점에서 가까운 정점부터 탐색한다.
- V가 정점의 수, E가 간선의 수일 때 BFS의 시간복잡도는 O(V + E)다.
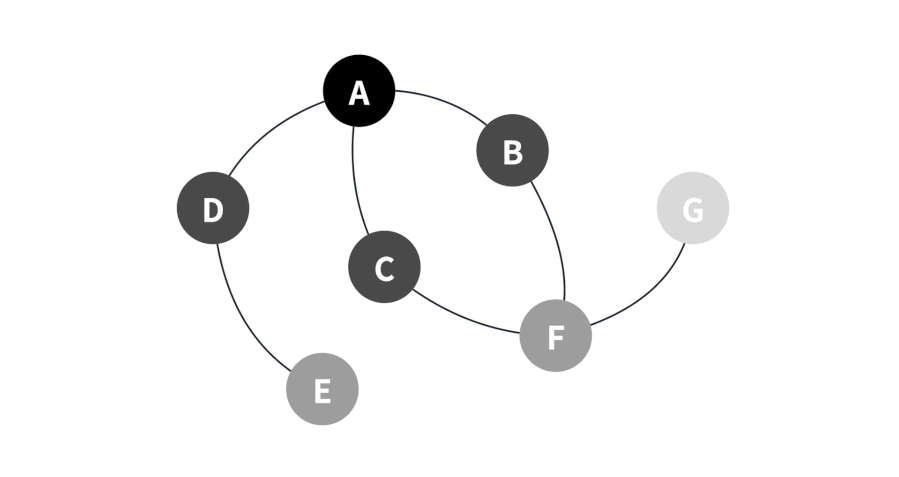
✔ 탐색할 그래프
const graph = {
A: ["B", "C", "D"],
B: ["A", "F"],
C: ["A", "F"],
D: ["A", "E"],
E: ["D"],
F: ["B", "C", "G"],
G: ["F"],
};🖥 BFS 구현 및 테스트 코드
// Queue를 이용한 너비 우선 탐색 알고리즘
const BFS = (graph, firstNode) => {
const visited = []; // 탐색을 마친 노드들을 저장할 queue
let nextNode = []; // 탐색해야할 노드들을 저장할 queue
nextNode.push(firstNode); // 노드 탐색 시작
while (nextNode.length !== 0) { // 모든 노드 탐색 완료 전까지
const node = nextNode.shift();
if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없을 때
visited.push(node);
nextNode = [...nextNode, ...graph[node]];
}
}
return visited;
};
console.log(BFS(graph, "A"));🖨 출력 결과
🤷♂️ 'nextNode = [...nextNode, ...graph[node]];' 에서 '...'은 대체 뭐죠...?
- 비구조화 할당 문법 중 하나인 [...] 혹은 {...}은 배열이나 객체의 속성을 해체하여 그 값을 개별 변수에 담을 수 있게 하는 자바스크립트 표현식(expression)이다. 배열 [], 혹은 객체 {} 안의 값을 편하게 꺼내 쓸 수 있는 문법이며 비구조화(구조분해) 할당에 대해서는 추후에 자세히 알아보도록 한다.
📌 깊이 우선 탐색(DFS)
🔷 그래프 탐색 알고리즘으로 최대한 깊은 정점부터 탐색하는 알고리즘
- Queue와 Stack을 이용하여 구현할 수 있다.
- 시작 정점에서 깊은 것 부터 찾는다.
- V가 정점의 수, E가 간선의 수일 때 DFS의 시간복잡도는 O(V + E)다.
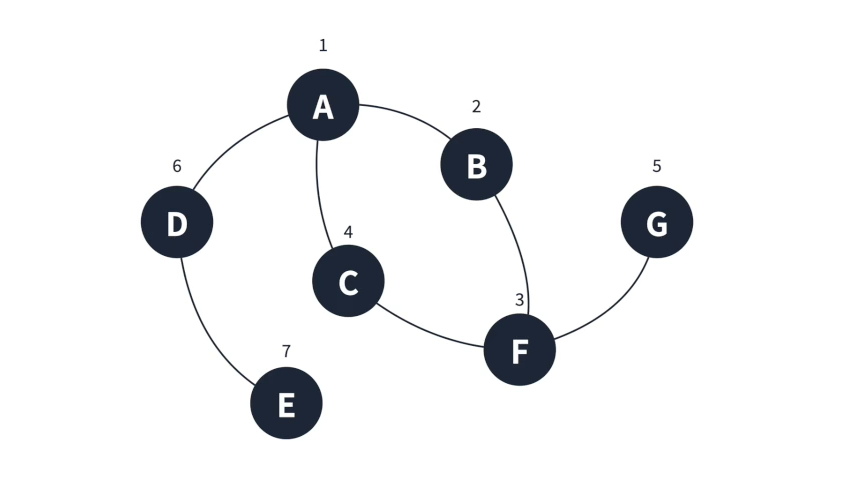
✔ 탐색할 그래프
const graph = {
A: ["B", "C", "D"],
B: ["A", "F"],
C: ["A", "F"],
D: ["A", "E"],
E: ["D"],
F: ["B", "C", "G"],
G: ["F"],
};🖥 DFS 구현 및 테스트 코드
// Queue와 Stack을 이용한 깊이 우선 탐색 알고리즘
const DFS = (graph, firstNode) => {
const visited = []; // 탐색을 마친 노드들을 저장할 queue
let nextNode = []; // 탐색해야할 노드들을 저장할 Stack
nextNode.push(firstNode); // 노드 탐색 시작
while (nextNode.length !== 0) { // 모든 노드 탐색 완료 전까지
const node = nextNode.pop();
if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없을 때
visited.push(node);
nextNode = [...nextNode, ...graph[node]];
}
}
return visited;
};
console.log(DFS(graph, "A"));🖨 출력 결과
❗ 그림의 출력 순서랑 다른 것 같은데요...?
그림이 잘못된 것으로 보입니다. 알고리즘에는 문제가 없습니다. 저게 올바른 출력입니다.
📌 그리디 알고리즘
🔷 매 선택에서 지금 이 순간 가장 최적인 답을 선택하는 알고리즘
- 특징
1) 보통 최적해를 구하는 알고리즘보다 빠른 경우가 많다.
2) 크루스칼, 다익스트라 알고리즘 등에 사용된다.
3) 직관적인 문제 풀이에 적합하다.❗ 그렇다고 해서 최적해를 보장해주지는 않는다.
- 사용하기 적합한 문제의 대표로 거스름돈 반환 문제가 있다.
- "동전 개수를 최소화하면서 거스름돈을 줄 수 있는 방법은?"
// 거스름돈 그리디 알고리즘
function change(n) {
let count = 0;
const arr = [500,100,50,10];
for(let item of arr){
count = count + Math.floor(n/item); //동전의 개수
n = n - item * Math.floor(n/item); // 남은 돈 계산
}
return count;
}📌 백트래킹 알고리즘
🔷 모든 경우의 수를 탐색하는 알고리즘
- DFS나 BFS를 이용할 수 있다.
- 효율을 위해 탐색하지 않아도 되는 곳을 미리 막는 것을 가지치기(Pruning)라고 한다.
- 탐색에서 순환(Cycle)이 발생할 수 있다면 BFS를 이용하는 것이 편하다.
- 자바스크립트는 재귀 효율이 나쁘기 때문에 DFS를 구현할 경우 스택을 이용하는 것이 좋다.
💡 코딩 테스트에선 이를 고려하여 재귀로 작성해도 풀 수 있도록 문제를 제출하는 경우도 있다.
🔷 작성 시
1) 모든 경우의 수를 찾을 수 있도록 코딩한다.
2) 이후 문제에서 특정한 조건을 만족하는 것만 탐색하도록 조건문을 작성한다.
3) 절대로 답이 될 수 없는 것은 탐색을 종료한다.
- 사용하기 적합한 문제의 대표로 N-Queen 문제가 있다.
- "길이가 N인 체스판 위에 N개의 퀸이 서로를 공격할 수 없도록 배치할 수 있는 경우의 수는?"

// N-queen 백트래킹 알고리즘
function check(queen, row) {
// 이전까지 두었던 퀸의 위치를 확인한다.
for (let i = 0; i < row; i += 1) {
// 행의 위치와 대각선의 위치를 체크한다.
if (queen[i] === queen[row] || Math.abs(queen[i] - queen[row]) === row - i) {
return false; // 둘 수 없다면 false
}
}
return true; // 모두 통과되면 true
}
function search(queen, row) {
const n = queen.length;
let count = 0;
if (n === row) { // 재귀의 탈출 조건(체스판의 끝)
return 1;
}
for (let col = 0; col < n; col += 1) { // 0부터 n까지 열을 돌면 둘 수 있게 만든다.
queen[row] = col; // 우선 퀸을 둔다
if (check(queen, row)) { // 퀸을 둘 수 있다면
count += search(queen, row + 1); // 다음 행으로 이동
}
}
return count;
}
function solution(n) {
// 미리 n개 만큼의 배열을 초기화한다. 0번 행부터 시작한다.
return search(Array.from({ length: n }, () => 0), 0);
}음... 중간중간 어려운 문법의 벽에 부딪히는 빈도가 늘고 있다.
한번 전체적으로 짚고 넘어갈 필요성이 느껴진다.
그림 제공: https://programmers.co.kr/