딥러닝 기본

1. Introduction

• 딥러닝에서 중요한 것은 구현, 수학, 논문-트렌드이다.

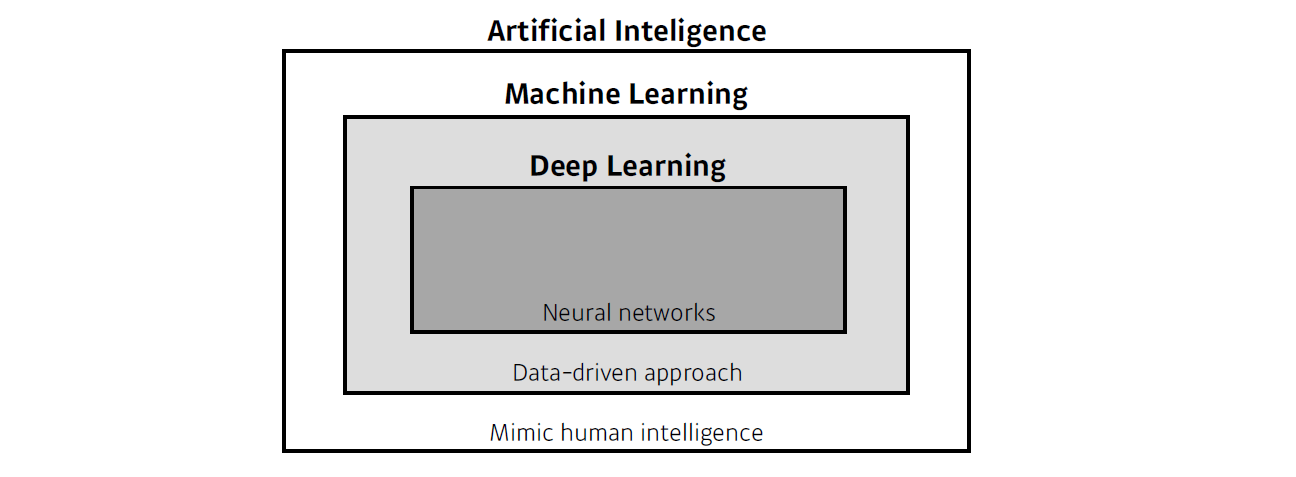
• AI의 방법론 중 하나가 ML, ML의 방법론 중 하나가 DL이다.

• DL의 중요한 요소는 data, model, loss, optimizer 이다.

• 위의 4가지 관점으로 논문을 바라보면, 기존 연구에 비해 어떤 장점이 있는지 알 수 있다.

1.1. Data

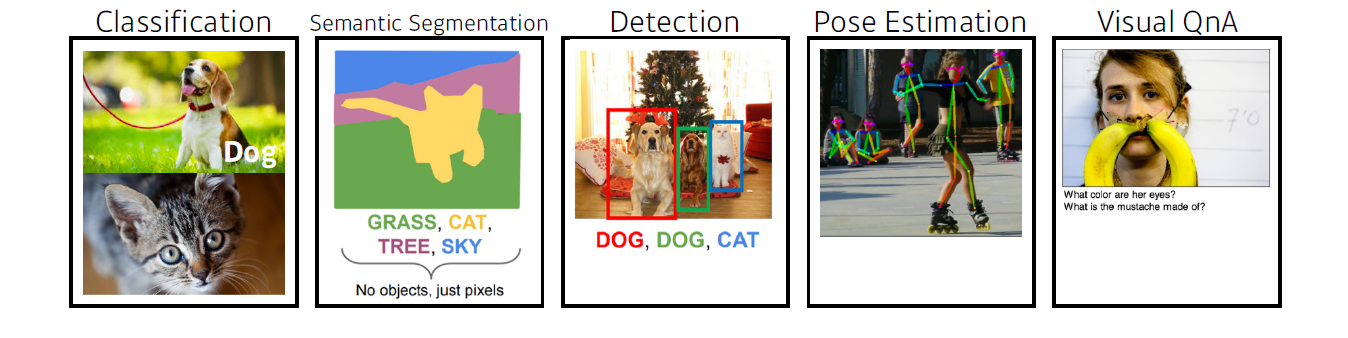
• 데이터는 해결하고자 하는 문제의 유형에 의존한다. 예를 들어 강아지와 고양이를 분류하기 위해선 이미지 데이터가 필요할 것이다.

• 문제의 유형으로는 Classification, Semantic Segmentation, Detection, Pose Estimation, Visual QnA 등이 있다.

1.2. Model

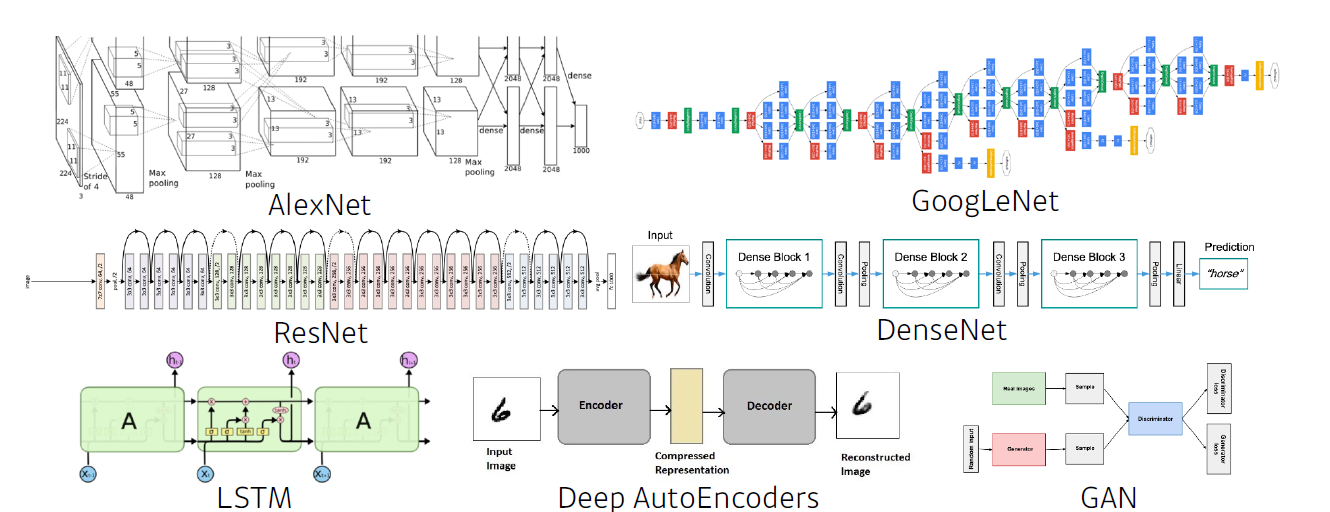
• 같은 데이터라도 모델의 성질에 다라 결과가 달라진다.

1.3. Loss

• Loss function은 이루고자 하는 것의 근사값이다.

• 데이터에 noise가 있을 수 있고 loss function은 근사치이기 때문에, 단순히 loss 값을 줄이는 것을 목표로 하면 안된다.

• Loss function에는 MSE, CE, MLE 등이 있는데 해당 함수들의 성질을 잘 이해해 목적에 맞게 선택해야 한다.

• 예로들어, MSE는 이상치에 민감하게 반응하므로 robust한 모델을 위한 loss function으로는 적합하지 않다.

1.4. Optimization Algorithm

• Optimizer algorithm의 종류로는 SGD, Momentum, NAG, Adagrad, Adadelta, Rmsprop 등이 있다.

• Optimizer algorithm의 특성을 잘 이해해서 목적에 맞게 잘 사용 해야 한다.

• 이외에도 Dropout, Early stopping, k-fold validation, weight decay, batch normalization, mixup, ensenble, bayesian optimization 등의 기법을 통해 최적화를 할 수 있다.

2. Histrocial Review

• 기계학습에 큰 변화를 준 모델들을 소개하겠다.

• 2012 - AlexNet
  

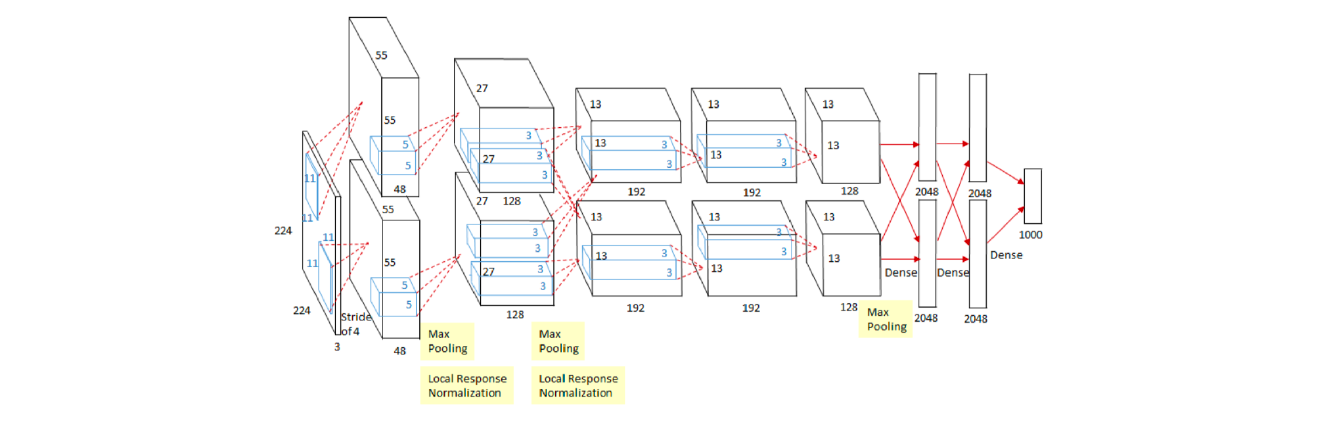
  • 해당 모델은 CNN으로 224 X 224 이미지를 분류하는 것이 목적이다.
  • 처음으로 딥러닝이 이미지 분류 대회에서 1등을 한 사건으로, 이후 계속 딥러닝이 1등을 차지했다.
  • 기계학습 판도가 바뀐 것이다.

• 2013 - DQN
  

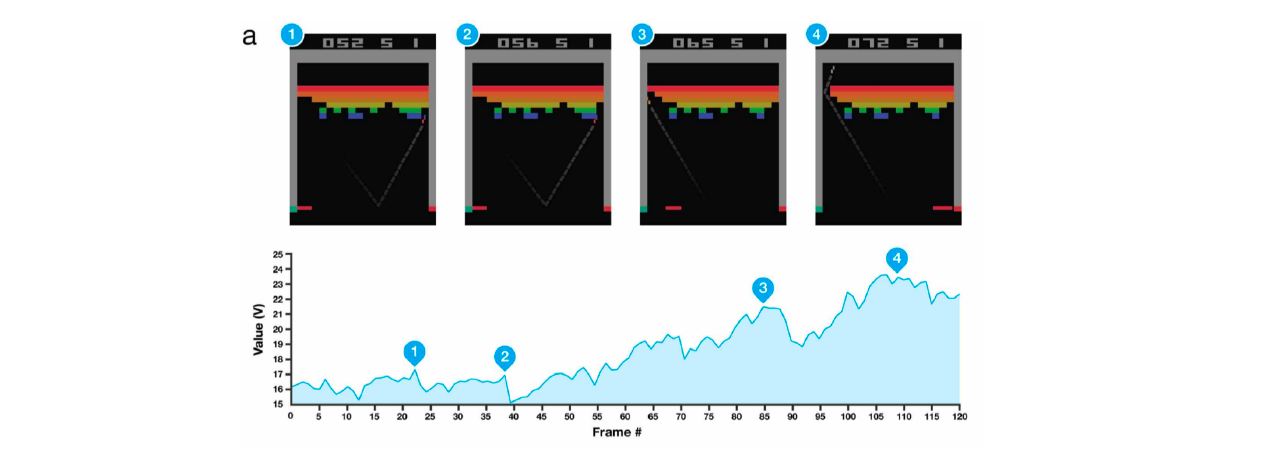
  • 딥마인드 회사에서 알파고에 사용한 알고리즘이다.
  • Q learning이라고 불리는 강화학습 방법론을 딥러닝에 접목했다.

• 2014 - Encoder / Decoder
  

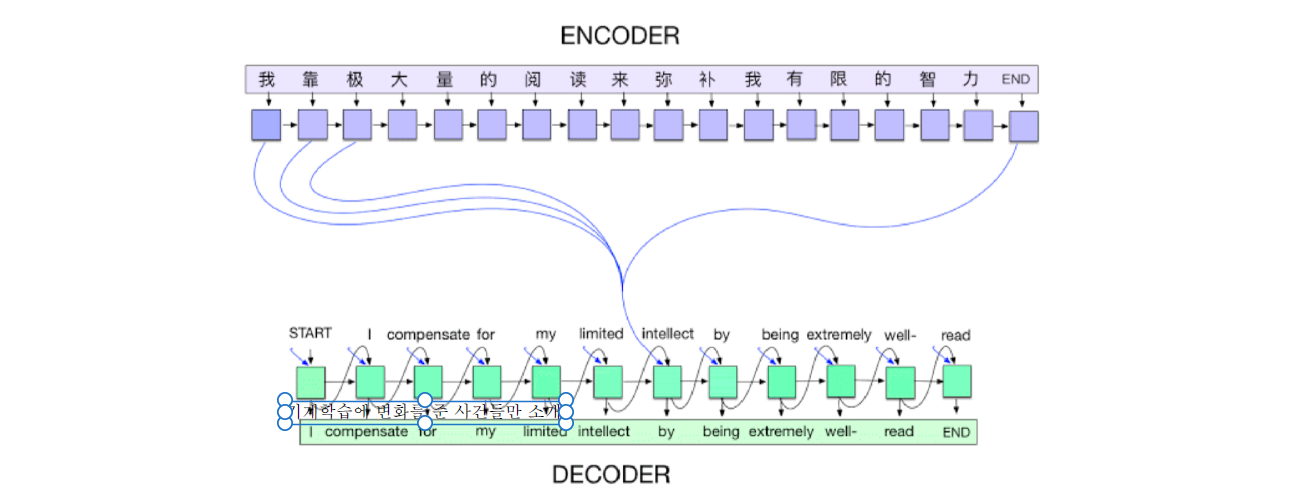
  • NLT(neural network translation)을 풀기위한 알고리즘이다.
  • Seq to seq 모델로, 단어의 연속이 주어졌을 때 다른 언어의 단어의 연속으로 표현한다.

• 2014 - Adam Optimizer
  

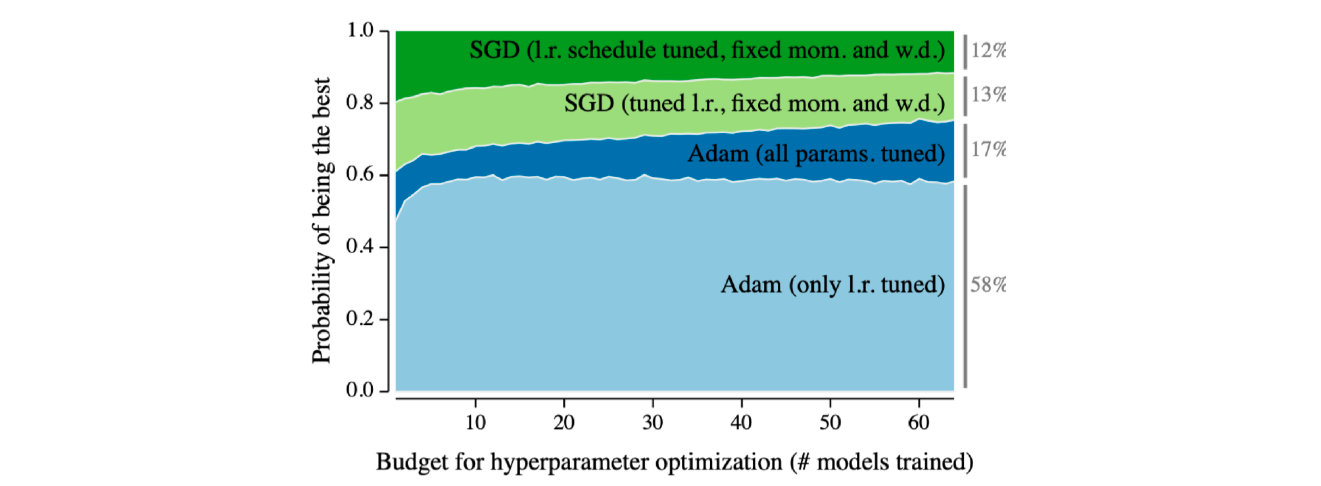
  • 실험적인 결과로 Adam이 많은 딥러닝 모델에서 사용되고, 그 성능이 제일 좋은 것으로 나온다.

• 2015 - GNN(Generative Adversarial Network)

  • GNN은 굉장히 중요하다.
  • 나중에 자세히 다루겠다.

• 2015 - Residual Networks
  

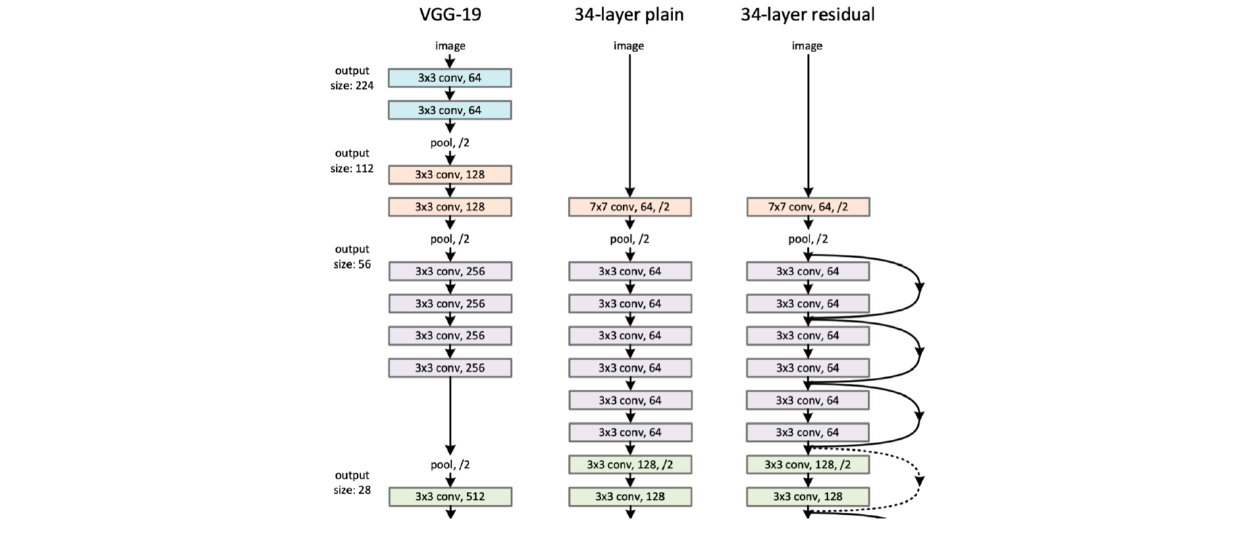
  • ResNet는 neural network를 쌓는 방법론으로 딥러닝의 딥러닝이 가능하도록 만들었다.
  • 이전에는 층이 깊어지면 overfitting이 된다는 고정관념이 있었지만, ResNet으로 overfitting을 극복했다.

• 2017 - Transformer

  • 오늘날 RNN의 대부분을 transformer 대체할 수 있다.
  • 이제 비전까지 넘보고 있다.

• 2018 - BERT(Bidirectional Encoder Representations from Transformers)

  • bidirectional 구조를 이용한 transformer이다.
  • fine-tuned NLP model로 이용된다.
  • fine-tuned란 transfer learning으로 미리 학습된 모델에 원하는 데이터를 학습시키는 것이다.
  • 예로들어, 위키백과의 말 뭉치를 통해 사전에 학습하고, 별로 없는 뉴스 기사 데이터를 학습시켜 기사를 작성하는데 좋은 성능을 내겠다.

• 2019 - BIG Language Models

  • BERT의 끝판왕으로, GPT-3는 1750억 개의 parameter를 가진다.

• 2020 - Self Supervised Learning
  

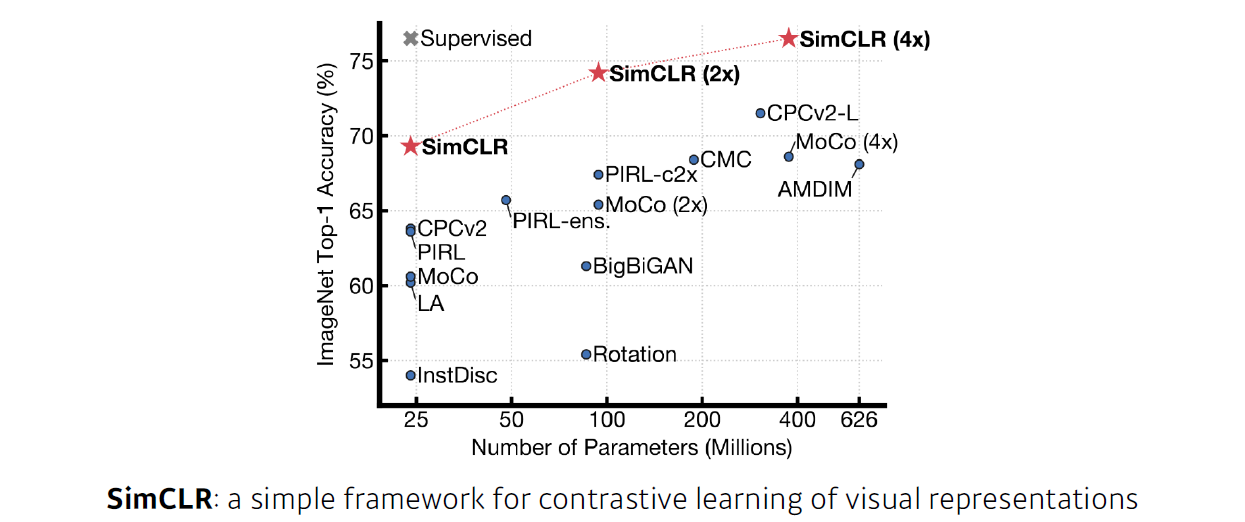
  • SimCLR은 구글에서 발표한 논문으로, 이미지 분류에서 한전된 학습 데이터 외에 label을 모르는 새로운 데이터를 학습에 같이 활용한다.
  • SimCLR은 visual representation(이미지를 컴퓨터가 잘 이해할 수 있는 벡터로 바꾸는 방법)이 목적이다. 이로 인해 원하는 목표를 더 잘 수행한다.(개, 고양이 분류 등)
  • Self supervised learning은 2가지 방법(visual representation, self superviesd data sampling)으로 활용된다.
  • Self superviesd data sampling는 풀고자 하는 문제를 굉장히 잘 알고 있을 때(고도화된 도메인 지식이 있을 때), 데이터를 만들어내는 것이다.

3. NN and MLP

• 처음에는 날기 위해 새를 모방했지만, 결국 비행기는 새를 닮지 않았다. 딥러닝도 시작은 사람의 뇌였지만, 현재는 그렇지 않다.

• Neural networks are function approximators that stack affine transformations followed by nonlinear transformations.

• 즉, NN은 affine 변환에 비선형 변환이 쌓인 function approximators이다.

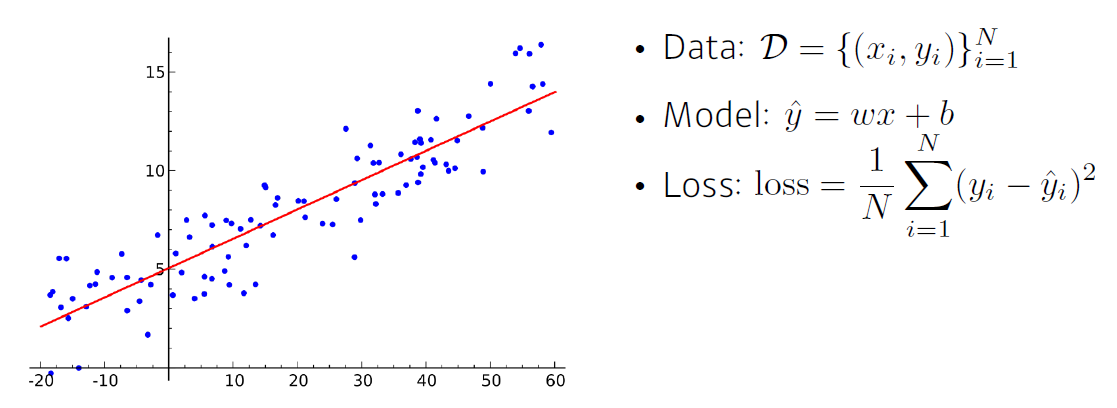
3.1. Linear Neural Networks

• loss가 최소가 되는 w, b를 바로 찾을 수 있다. ex) 역행렬 곱하기

• 그렇지만, 데이터가 적고 loss가 convex하고 모델이 linear해야 한다는 등 많은 제약 조건이 붙는다.

• 역전파를 사용하자.

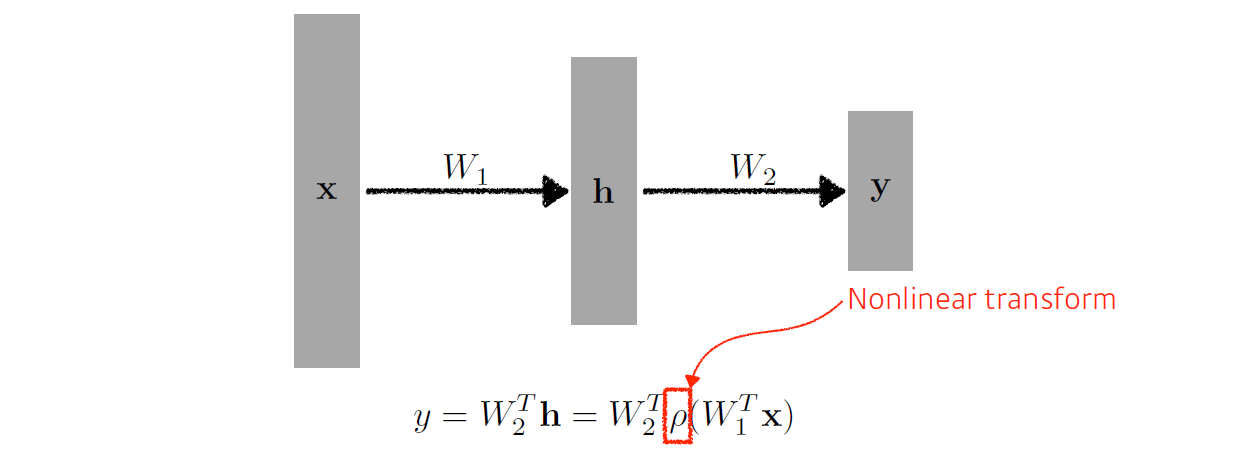
• 층을 쌓을 때 nonlinear transform(활성함수)를 사용하지 않으면, $W_2^TW_1^T$는 또다른 행렬이 되므로 층을 쌓는 의미가 없어진다.

• Hidden layer가 1개 있는 NN의 표현력은 일반적인 continuous function을 다 포함한다. 즉 원하는 function을 표현하는 NN은 어딘가에는 존재하는데 그것을 찾아야한다.

• 그만큼 NN의 표현력이 크고, 그렇기 때문에 잘 된다.