최적화

c0natus·2022년 2월 7일
DL Basic
0

DL Basic

목록 보기
2/2

  • 최적화에서 사용하는 용어를 제대로 알고 있지 않으면 나중에 잘못된 이해를 할 수 있으므로, 용어의 정의를 명확히 알아야 한다.

  • Gradient Descent의 정의는 다음과 같다.

First-order iterative optimization algorithm for finding a local minimum of a differentiable function.

1. 최적화에서 중요한 개념

1.1. Generalization

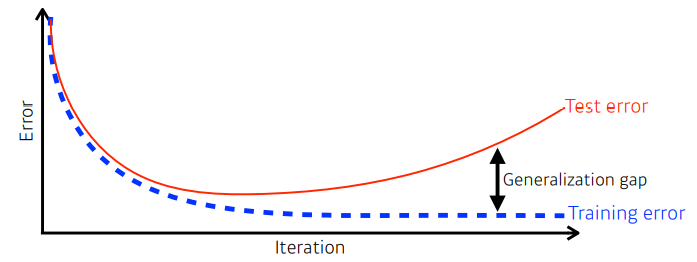
  • 일반화(generalization)은 학습하지 않은 데이터에 대해 얼마나 잘 작동하는 가를 말한다.

1.2. overfitting vs underfitting

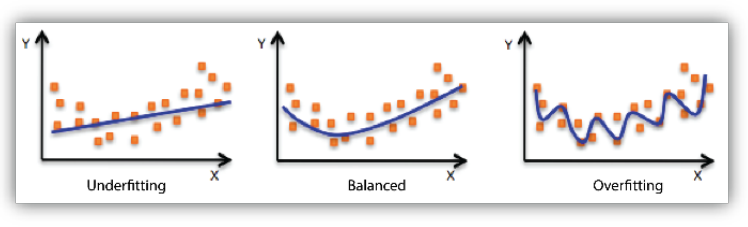
  • Target이 어떻게 생겼는지 모른다. overfitting 된 것이 궁극적으로 target을 표현할 수도 있다. 즉, overfitting, underfitting은 이론적인 얘기이다.

  • Overfitting은 학습된 데이터는 잘 맞추지만, test data에 대해서는 잘 작동하지 않는 것을 말한다.

1.3. Cross-validation

  • Cross-validation은 test data set에 대해 얼마나 일반화가 잘 되었는지를 평가하는 방법론이다.

  • Cross-validation으로 최적의 hyperparameter를 찾고, 학습 시킬 때는 모든 데이터를 활용한다.

1.4.Bias and Variance

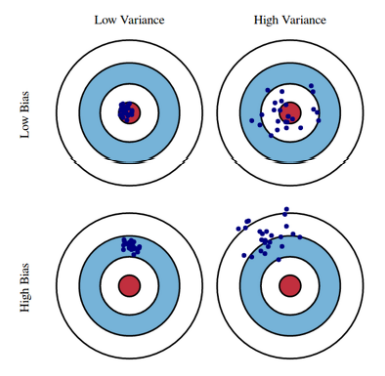
  • Variance은 비슷한 입력을 넣었을 때 얼마나 일관되게 출력이 나오는 지를 나타낸다.

  • 보통 간단한 모델이 variance가 낮다.

  • Bias는 평균적으로 봤을 때 예측 값들이 target 근처면, bias가 낮다고 한다.

  • Bias와 variance은 tradeoff 관계이다.

  • 학습 데이터에 noise가 있다고 가정 했을 때, 해당 데이터의 loss 값을 최소화 하는 것은 3가지 부분으로 나뉜다.

  • Cost를 최소화 할 때, 실제로 cost는 3부분으로 이뤄져 있다. 이때, 한 부분을 최소화하면 다른 부분이 증가한다.

  • t는 noise가 있는 데이터이다. 위의 수식은 데이터에 noise가 있을 때, bias와 variance를 둘 다 줄이는 것은 힘들다는 것을 말한다.

1.5. Bootstrapping

  • Bootstrapping은 통계학에서 자주 사용되는 용어이다.

Bootstrapping is any test or metric that uses random sampling with replacement.

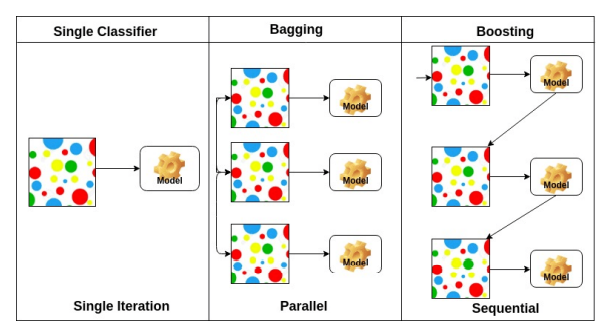
Bagging(Bootstrapping aggregating)

  • 학습 데이터를 일부만 사용해 여러개의 sub 학습 데이터로 여러 개의 모델을 만든다.

  • 입력에 대한 모델들의 출력의 평균을 사용하거나 voting을 하겠다.

  • 기본적인 앙상블 기법, 캐글에서 많이 사용한다.

Boosting

  • 간단한 모델들을 여러개 만든다. 이때, 현재 모델에서 잘 예측하지 못한 데이터에 대해서만 잘 동작하는 모델을 다음 순서에 만든다.

  • 이처럼 weak leaners를 여러개 만들어 sequencital하게 합쳐서 하나의 strong learner를 만든다.

2. Gradient Descent 방법론들

2.1. Batch Size로 구분

Stochastic gradient descent

  • Update with the gradient computed from a single sample.

Mini-batch gradient descent

  • Update with the gradient computed from a subset of data.

  • 대부분 사용하는 방법론이다.

Batch gradient descent

  • Update with the gradient computed from the whole data.

Batch-size Matter

  • On Large-batch Training for Deep Learning: Generalization Gap and Sharp Minima, 2017 논문에 따르면, 큰 batch 방법론들은 sharp minimizers에 수렴하는 경향이 있고 작은 batch 방법론들은 flat minimizers에 수렴하는 경향이 있다는 것을 실험을 통해서 발견 되었다.

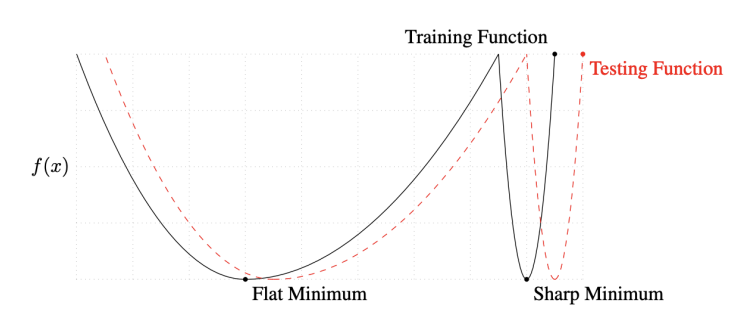
  • 논문에서는 flat minimizer가 더 좋다고 말하고 있다.

  • training function의 flat minimum 지점은 test function에서도 적당한 낮은 값이 나온다.

  • sharp minimum은 train에서는 낮을 지라도 test function에서 높은 값이 나온다.

  • 즉 generalization performance가 떨어진다.

  • 해당 논문에서는 이러한 점을 해결하기 위해, 큰 batch size를 활용하는 기법들을 소개해준다.

2.2. Update 하는 방법(algorithm)으로 구분

Stochastic gradient descent

Wt+1←Wt−ηgtW_{t+1} \leftarrow W_{t} - \eta g_t

  • η\eta는 learning rate(=step size), gtg_t는 gradient이다.

  • 해당 방법은 learning rate를 결정하기 어렵다는 단점이 있다.

Momentum

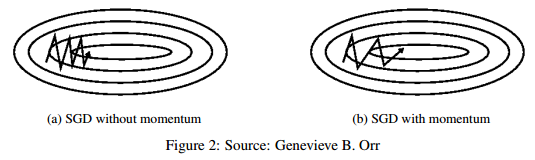
  • SGD는 기울기가 높은 평면에서 최적값을 향해 잘 찾아가지 못한다. 위 그림처럼 경사도의 기울기를 따라 왔다갔다 하는 것을 확인할 수 있다.

  • Momentum은 최적값의 방향으로 SGD가 가속하도록 도와주고 위 그림에서 보이는 진동을 완화시키는 방법이다.

at+1←βat+gta_{t+1} \leftarrow \beta a_t + g_t
Wt+1←Wt−ηat+1W_{t+1} \leftarrow W_t - \eta a_{t+1}

  • momentum은 관성이라는 뜻이다.

  • at+1a_{t+1}은 accumulation, β\beta는 momentum, ata_t는 바로 이전 gradient, gtg_t는 현재 gradient이다.

  • 이전 gradient를 참고해 gradient가 흐르던 방향을 유지시켜 준다.

  • SGD의 수식과 비교하면, momentum 항인 βat\beta a_t을 추가적으로 빼준 것을 확인할 수 있다. 이 변수가 내리막길에서는 가속하도록 도와주고, 방향이 바뀌었을 때 파라미터가 갱신하는 양을 감소시킨다.

Nesterov Accelerated Gradient

  • NAG는 멈춰야할 시기에 더 나아가지 않고 제동을 거는 방법이다.

at+1←βat+▽L(Wt−ηβat)a_{t+1} \leftarrow \beta a_t + \triangledown \mathcal{L}(W_t - \eta \beta a_t)
Wt+1←Wt−ηat+1W_{t+1} \leftarrow W_t - \eta a_{t+1}

  • ▽L(Wt−ηβat)\triangledown \mathcal{L}(W_t - \eta \beta a_t)를 Lookahead gradient라고 한다.

  • momentum은 현재의 gradient를 가지고 momentum을 accumulation 했다.

  • 하지만, NAG는 현재의 gradient를 가지고 그곳으로 한번 가보고, 간 곳에서의 gradient(lookahead gradient)를 가지고 accumulation 한다.

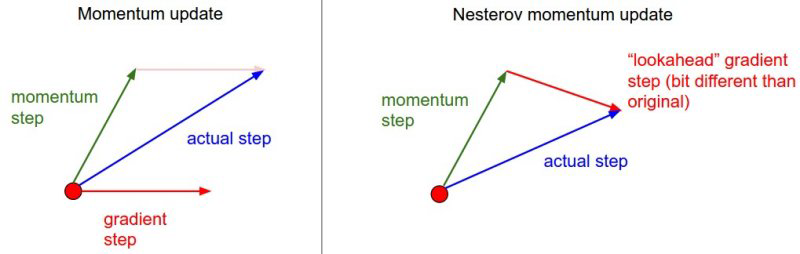
  • Momentum은 현재 기울기를 계산하고 모멘텀을 적용시켜 그 방향으로 크게 이동한다.

  • NAG는 Momentum 위치에서 다음 위치를 예측하여 파라미터를 갱신한다.

  • 그림에서 보듯이 NAG는 Momentum과 비교하여 보면 상대적으로 느린 속도로 값이 갱신된다는 것을 확인할 수 있고, 너무 빠르게 기울기가 수정되는 것을 방지할 수 있다.

  • 그리고 NAG는 RNN의 성능을 크게 증가시켰다고 말한다.

지금까지 알아본 알고리즘은 손실 함수의 기울기로 갱신을 하였고, SGD의 속도를 향상시켰다.
이제 매개변수의 중요성에 따라 각각의 매개변수에 가중치를 두어 갱신을 하는 알고리즘에 대해 알아보자.

Adagrad

Adagrad adapts the learning rate, performing larger updates for infrequent and smaller updates for frequent parameters.

  • Adagrad는 많이 변한 파라미터는 적게 변화시키고, 적게 변한 파라미터는 많이 변화시킨다.

Wt+1=Wt−ηGt+ϵgtW_{t+1} = W_t - \frac{\eta}{\sqrt{G_t + \epsilon}}g_t

  • GtG_t는 Sum of gradients squares로 지금까지 얼마나 변했는지를 제곱해서 더한 값이다.

  • GtG_t는 계속해서 커지는데 분모에 있으므로, 파라미터가 많이 변해 값이 커지면 점점 더 적게 변화시킨다.

  • ϵ\epsilon은 0으로 나눠지는 것을 방지한다.

  • Adagrad는 학습이 길어지면, GtG_t가 무한대로 가서 학습이 일어나지 않게 된다는 문제가 있다.

  • 이것을 해결하기 위해 Adam이 등장했다.

Adadelta

Adadelta extends Adagrad to reduce its monotonically decreasing the learning rate by restricting the accumulation window.

  • EMA(exponential moving averate)로 GtG_t를 업데이터 하는 방법론이다.

  • GtG_t가 계속 커지는 것을 막기 위한 방법론으로, 특정 사이즈(window size)만큼의 과거 기록만 가지고 있는 것이 있다.

  • 하지만 GPT-3 처럼 파라미터 수가 많으면, 파라미터 수 * window size 만큼 GPU가 필요해진다.

  • 이것을 그나마 막을 수 있는 방법이 EMA(exponential moving average)이다.

Gt=γGt−1+(1−γ)gt2G_t = \gamma G_{t-1} + (1-\gamma)g_t^2
Wt+1=Wt−Ht−1+ϵGt+ϵgtW_{t+1} = W_t - \frac{\sqrt{H_{t-1} + \epsilon}}{\sqrt{G_t + \epsilon}}g_t
Ht=γHt−1+(1−γ)(△Wt)2H_t = \gamma H_{t-1} + (1-\gamma)(\triangle W_t)^2

  • GtG_t는 gradient squares의 EMA이다.

  • HtH_t는 difference squares의 EMA이다.

  • Adadelta는 learning rate가 없다. 즉, 바꿀 수 있는 요소가 없다 → 잘 사용되지 않는다.

RMSprop

  • Geoff Hinto이 논문이 아니라 강의에서 자신의 경험을 살려 해당 방법론을 소개했다.

Gt=γGt−1+(1−γ)gt2G_t = \gamma G_{t-1} + (1-\gamma)g_t^2
Wt+1=Wt−ηGt+ϵgtW_{t+1} = W_t - \frac{\eta}{\sqrt{G_t + \epsilon}}g_t

Adam

Adaptive Moment Estimation (Adam) leverages both past gradients and squared gradients.

  • 가장 많이 쓰이는 알고리즘이다.

mt=β1mt−1+(1−β1)gtm_t = \beta_1m_{t-1} + (1-\beta_1)g_t
vt=β2vt−1+(1−β2)gt2v_t = \beta_2v_{t-1} + (1-\beta_2)g_t^2
Wt+1=Wt−ηvt+ϵ1−βs2t1−β1tmtW_{t+1} = W_t - \frac{\eta}{\sqrt{v_t + \epsilon}}\frac{\sqrt{1-\beta s_2^t}}{1-\beta_1^t}m_t

  • mtm_t는 momentum이고, vtv_t는 EMA of gradient squares, η\eta는 learning rate이다.

  • 1−βs2t1−β1t\frac{\sqrt{1-\beta s_2^t}}{1-\beta_1^t}는 전체 gradient descent가 unbiased estimator가 되기 위해 팔요한 것으로, 중요한 값은 아니다.

  • Hyperparameter는 총 4개로, β1,β2,η,ϵ\beta_1, \beta_2, \eta, \epsilon이 있다.

  • Adam은 momentum과 adpative learning rate 방법론을 효과적으로 결합한 것이다.

3. Regularization 방법론

  • Regularization은 overfitting을 방지해 generalization performance를 높여준다.

  • 모델에 넣어서 사용해보고 잘 되면 쓰고, 안 되면 쓰지 말자. → 실험적으로 사용하자.

3.1. Early stopping

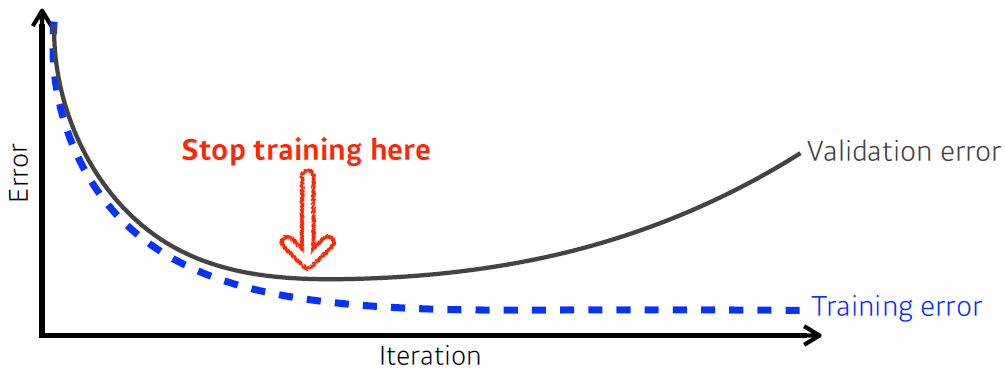
  • Early stopping을 하기 위해선, validation data가 필요하다.

  • 해당 기법은 validation error와 training error의 차이가 많이 벌어지는 부분에서 학습을 멈춘다.

3.2. Parameter Norm Penalty

  • weight decay와 같은 말로, nerual network의 parameter가 너무 커지지 않게 규제를 가해서 nerual network가 만들어내는 function space에서 최대한 부드러운 loss function을 만든다.

total cost=loss(D∣W)+α2∣∣W∣∣22\text{total cost} = \text{loss}(\mathcal{D}|W) + \frac{\alpha}{2}||W||^2_2

  • α2∣∣W∣∣22\frac{\alpha}{2}||W||^2_2가 parameter norm penalty이다.

  • 네트워크 파라미터를 전부 제곱 한다음 더하면 큰 수가 나오는데, 이 값을 줄이는 것이다.

  • 부드러운 함수일수록 generalization performance가 높을 것이라고 예측한다.

References

profile
c0natus
Done is Better Than Perfect
이전 포스트

딥러닝 기본

0개의 댓글