RNN 첫 걸음

c0natus·2022년 1월 29일
ai math
0

AI Math

목록 보기
9/9

1. 시퀀스(sequence) 데이터

  • 시계열 데이터, 시퀀스 데이터는 i.i.d(독립 동등 분포)가 아니라 서로 종속된 데이터이다.

  • 이러한 데이터를 분석하는 데 사용하는 것이 RNN이다.

  • 소리, 문자열, 주가 등의 데이터를 시퀀스 데이터로 분류한다.

  • 시퀀스 데이터는 순서를 바꾸거나 과거 정보에 손실이 발생하면, 데이터의 확률분포도 바뀌게 된다.

  • 과거 정보 또는 앞뒤 맥락 없이 미래를 예측하거나, 문장을 완성하는 건 불가능하다.

  • 이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해 조건부확률을 이용할 수 있다.


P(X1,⋯ ,Xt)=∏s=1tP(Xs∣X1,⋯ ,Xs−1)P(X_1,\cdots,X_t) = \prod\limits_{s=1}^tP(X_s|X_1,\cdots,X_{s-1})

  • 결국, X1,⋯ ,Xt−1X_1,\cdots,X_{t-1} 데이터가 있을 때, Xt∼P(Xt∣X1,⋯ ,Xt−1)X_t \sim P(X_t|X_1,\cdots,X_{t-1})인 XtX_t를 모델링해야 한다.

2. Autoregressive Model

  • 조건부확률은 과거의 모든 정보를 사용해, 가변적인 데이터를 다룰 수 있는 모델이 필요하다.
  • 하지만, 시퀀스 데이터를 분석할 때 과거의 모든 정보들이 필요한 것은 아니다.

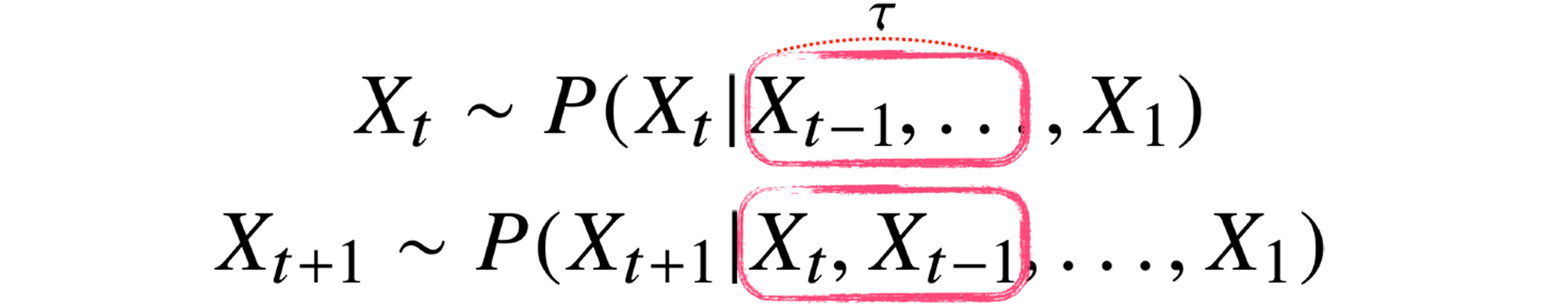
  • 고정된 길이 τ\tau만큼의 시퀀스만 사용하는 경우 AR(τ\tau) 자기회귀모델(Auto Regressive Model)이라고 부른다.

  • τ\tau 는 hyperparameter이기 때문에 문제에 따라 그 값이 다르고, τ\tau 를 결정할 때 사전지식이 필요하다.

3. Latent Auto Regressive Model

  • 만약 시퀀스 데이터를 분석할 때 먼 과거의 정보까지 필요하면 어떻게 할까?

  • 위의 경우 해당 포스트에서 배우게 될, RNN의 기본형인 잠재자기회귀모델(Latent Auto Regressive Model)을 사용한다.

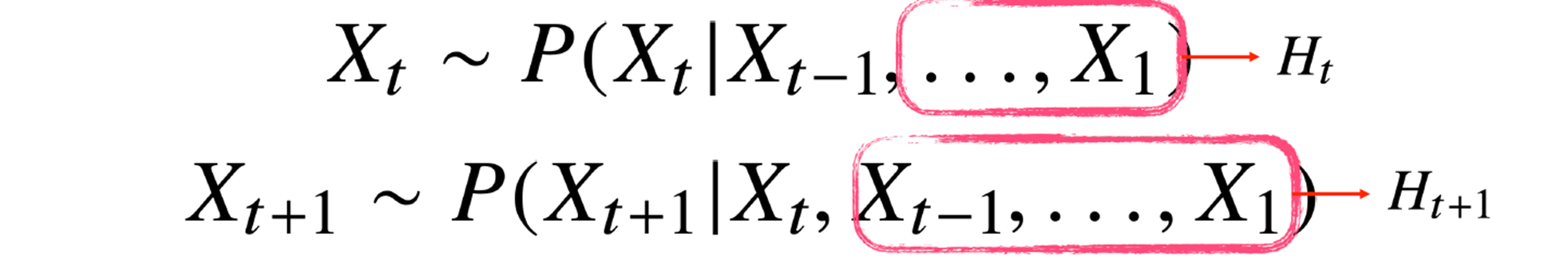
  • 잠재AR모델은 바로 이전 정보를 제외한 나머지 정보들을 HtH_t라는 잠재변수로 인코딩해서 활용한다.

  • 해당 모델은 과거의 모든 데이터를 활용할 수 있고, 고정된 길이의 데이터를 가진고 모델링할 수 있다는 장점이 있다.

  • 해당 모델은 잠재변수 HtH_t를 어떻게 인코딩 해야할 지 정해야 한다.

  • 잠재변수 HtH_t를 신경망을 통해 반복해서 사용하여 시퀀스 데이터의 패턴을 학습하는 모델이 RNN이다.

Ht=Netθ(Ht−1,Xt−1)H_t = Net_{\theta}(H_{t-1}, X_{t-1})

4. RNN(Recurrent Neural Network)

  • 가장 기본적인 RNN 모형은 MLP와 유사하다.
O=HW(2)+b(2)H=σ(XW(1)+b(1))\boldsymbol{O} = \boldsymbol{HW}^{(2)} + \boldsymbol{b}^{(2)} \\ \boldsymbol{H} = \sigma(\boldsymbol{XW}^{(1)} + \boldsymbol{b}^{(1)})

  • W(1)\boldsymbol{W}^{(1)}과 W(2)\boldsymbol{W}^{(2)}은 시퀀스와 상관없이 불변인 행렬이다.

  • RNN은 이전 순서의 잠재변수와 현재의 입력을 활용해 모델링한다.

4.1. Forward Propagation

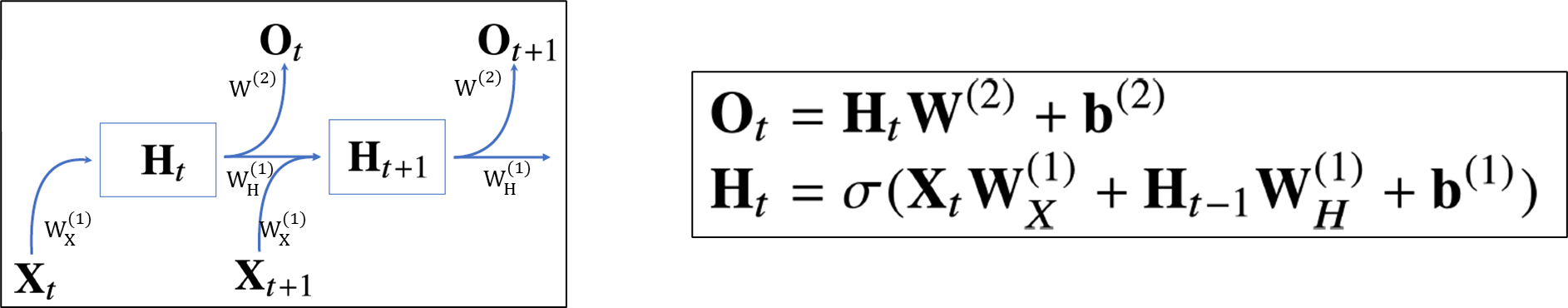
  • 잠재변수인 HtH_t를 복제해 다음 순서의 잠재변수를 인코딩하는데 사용한다.

  • 3개의 가중치 행렬 WX(1)W_X^{(1)}, WH(1)W_H^{(1)}, W(2)W^{(2)}는 tt 에 따라 변하지 않는다.

4.2. BPTT(Back Propagation Through Time)

  • RNN의 역전파는 잠재변수의 연결그래프에 따라 순차적으로 계산한다.

  • 마지막 예측까지 모두 이뤄지고 마지막 시점에서의 gradient가 과거까지 전달되는데, 이를 BPTT라 하며 RNN의 역전파 방법이다.

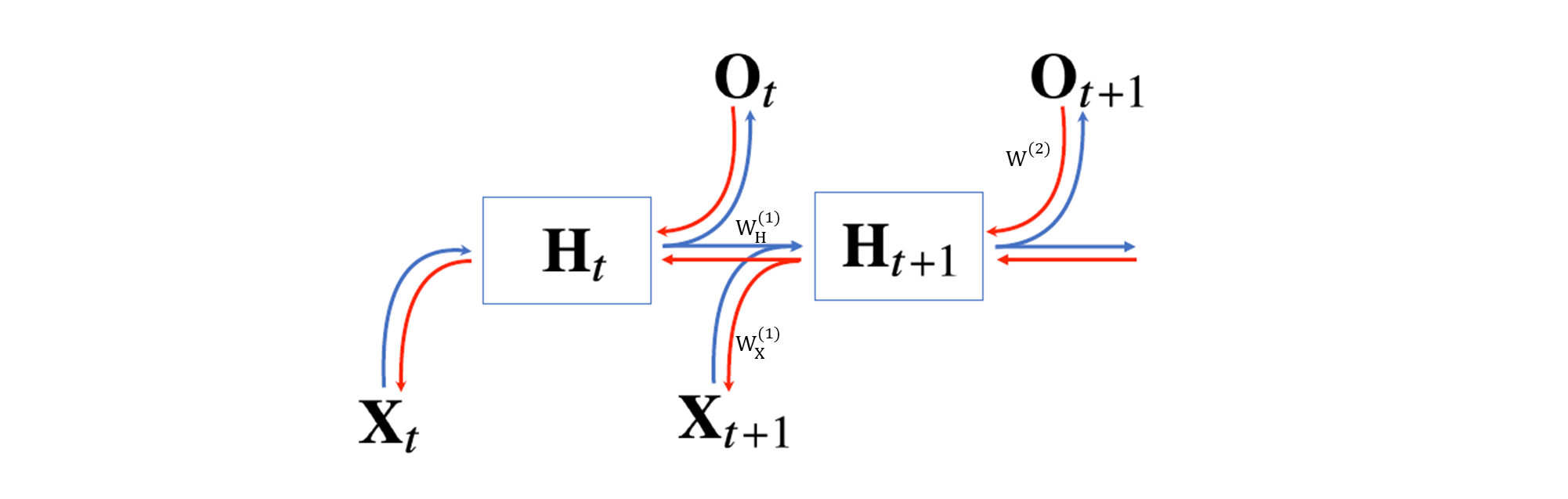
  • 잠재변수에는 총 2개의 gradient vector가 들어온다.
    1. 다음 시점의 잠재변수에 들어오는 gradient vector
    2. 출력에서 들어오는 gradient vector
  • BPTT를 통해 RNN의 WH(1)W_H^{(1)}에 대해 미분을 계산하면 아래와 같다.

L(x,y,WH(1),W(2))=∑t=1Tl(yt,ot)L(x,y,W_H^{(1)}, W^{(2)}) = \sum\limits_{t=1}^T\mathcal{l}(y_t, o_t)

  • RNN의 손실함수는 모든 시점에서의 손실함수를 구한 뒤, 더한다.

  • ht=f(xt,ht−1,WH(1))h_t = f(x_t, h_{t-1}, W_H^{(1)}),   ot=g(ht,W(2))\ \ o_t = g(h_t, W^{(2)})이다.


∂L(x,y,WH(1),W(2))∂WH(1)=∑t=1T∂l(yt,ot)∂WH(1)\frac{\partial L(x,y,W_H^{(1)}, W^{(2)})}{\partial W_H^{(1)}} = \sum\limits_{t=1}^T\frac{\partial \mathcal{l}(y_t, o_t)}{\partial W_H^{(1)}}

∂l(yt,ot)∂WH(1)=∂l(yt,ot)∂ot∂ot∂WH(1)=∂l(yt,ot)∂ot∂g(ht,W(2))∂WH(1)\frac{\partial \mathcal{l}(y_t, o_t)}{\partial W_H^{(1)}} = \frac{\partial \mathcal{l}(y_t, o_t)}{\partial o_t} \frac{\partial o_t}{\partial W_H^{(1)}} = \frac{\partial \mathcal{l}(y_t, o_t)}{\partial o_t} \frac{\partial g(h_t, W^{(2)})}{\partial W_H^{(1)}}

  • HtH_t는 WH(1)W_H^{(1)}에 영향을 받지만, W(2)W^{(2)}는 WH(1)W_H^{(1)}와 관련이 없다.

∂g(ht,W(2))∂WH(1)=∂g(ht,W(2))∂ht∂ht∂WH(1)\frac{\partial g(h_t, W^{(2)})}{\partial W_H^{(1)}} = \frac{\partial g(h_t, W^{(2)})}{\partial h_t} \frac{\partial h_t}{\partial W_H^{(1)}}

∴∂L(x,y,WH(1),W(2))∂WH(1)=∑t=1T∂l(yt,ot)∂ot∂g(ht,W(2))∂ht∂ht∂WH(1)\therefore \frac{\partial L(x,y,W_H^{(1)}, W^{(2)})}{\partial W_H^{(1)}} = \sum\limits_{t=1}^T\frac{\partial \mathcal{l}(y_t, o_t)}{\partial o_t} \frac{\partial g(h_t, W^{(2)})}{\partial h_t} \frac{\partial h_t}{\partial W_H^{(1)}}

  • 이제 ∂ht∂WH(1)\frac{\partial h_t}{\partial W_H^{(1)}}의 값을 구해보자.

  • ht=f(xt,ht−1,WH(1))h_t = f(x_t, h_{t-1}, W_H^{(1)})이고, 단순히 ht−1h_{t-1}를 상수 취급한다면, ∂ht∂WH(1)=∂f(xt,ht−1,WH(1))∂WH(1)\frac{\partial h_t}{\partial W_H^{(1)}} =\frac{\partial f(x_t, h_{t-1}, W_H^{(1)})}{\partial W_H^{(1)}}일 것이다.

  • 하지만, ht−1h_{t-1}에도 WH(1)W_H^{(1)}가 영향을 끼치므로 무시하면 안된다.


∂ht∂WH(1)=∂f(xt,ht−1,WH(1))∂WH(1)+∂ht∂ht−1⋅∂ht−1∂WH(1)\frac{\partial h_t}{\partial W_H^{(1)}} = \frac{\partial f(x_t, h_{t-1}, W_H^{(1)})}{\partial W_H^{(1)}} + \frac{\partial h_t}{\partial h_{t-1}} \cdot \frac{\partial h_{t-1}}{\partial W_H^{(1)}}

∵ f(xt,ht−1,WH(1))=∂ht∂ht−1×ht−1+⋯\because \ f(x_t, h_{t-1}, W_H^{(1)}) = \frac{\partial h_t}{\partial h_{t-1}} \times h_{t-1} + \cdots

  • ∂ht∂ht−1\frac{\partial h_t}{\partial h_{t-1}}은 ht−1h_{t-1}의 계수로 생각할 수 있다.

  • ht−1WH(1)\frac{h_{t-1}}{W_H^{(1)}}도 이전과 같은 방법으로 전개가 될 것이다


∴∂ht∂WH(1)=∂f(xt,ht−1,WH(1))∂WH(1)+∑i=1t−1(∏j=i+1t∂f(xj,hj−1,wh)∂hj−1)∂f(xi,hi−1,wh)∂WH(1)\therefore \frac{\partial h_t}{\partial W_H^{(1)}} = \frac{\partial f(x_t, h_{t-1}, W_H^{(1)})}{\partial W_H^{(1)}} + \sum\limits_{i=1}^{t-1}\Bigg(\prod\limits_{j=i+1}^t\frac{\partial f(x_j, h_{j-1}, w_h)}{\partial h_{j-1}}\Bigg)\frac{\partial f(x_i, h_{i-1}, w_h)}{\partial W_H^{(1)}}

  • 하지만, 시퀀스 길이가 길어질수록 ∏j=i+1t∂f(xj,hj−1,wh)∂hj−1\prod\limits_{j=i+1}^t\frac{\partial f(x_j, h_{j-1}, w_h)}{\partial h_{j-1}}은 불안정해지기 쉽다.

  • 만약 ∂f(xj,hj−1,wh)∂hj−1\frac{\partial f(x_j, h_{j-1}, w_h)}{\partial h_{j-1}}의 값들이 1보다 크면 크기가 매우 커지고, 1보다 작으면 크기가 매우 작아지기 때문이다.

  • 이것은 기울기 소실(Gradient Vanishing)과 폭주(Exploding)라고 한다.

  • 특히 기울기 소실이 일어나면, 미래의 결과를 과거에 반영하기 쉽지 않기 때문에 과거 정보를 유지할 확률이 높다.

  • 시퀀스 길이가 길어지는 경우 BPTT를 통한 역전파 알고리즘의 계산이 불안정 해지므로 길이를 끊는 것이 필요하다. 즉, 특정 시점부터 미래의 gradient를 전달받지 않는 것이다.

  • 이를 truncated BPTT라고 한다.

  • 하지만 이것은 기울기 소실을 완전히 해결할 수 없다.

  • 길이가 긴 시퀀스 데이터의 기울기 소실 문제를 해결하기 위해 등장한 RNN이 LSTM과 GRU이다.

profile
c0natus
Done is Better Than Perfect
이전 포스트

CNN 첫 걸음

0개의 댓글