1. Convolution 연산
-
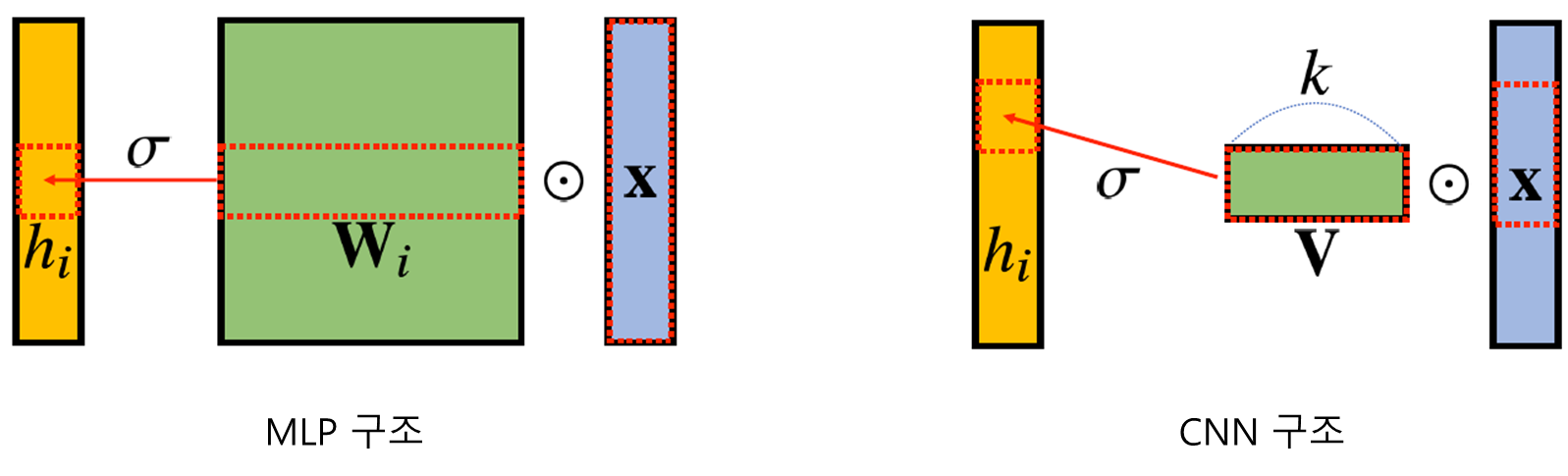
MLP는 각 뉴런들이 선형모델과 활성함수로 모두 연결된(fully connected) 구조이다.
-
MLP는 각 성분 에 대응하는 가중치 행 가 필요하다.
-
Convolution 연산은 이와 달리 커널(kernel)을 입력벡터 상에서 움직여가면서, 선형모델과 활성함수가 적용되는 구조이다.
-
Convolution 연산은 모든 에 대해 적용되는 커널은 로 같고, 커널의 사이즈 만큼 상에서 이동하면서 적용한다.
-
Convolution 연산의
수학적인 의미는 신호(signal)를 커널을 이용해 국소적으로증폭 또는 감소시켜서 정보를추출또는필터링하는 것이다.
신호에 해당하는 것이 이고,커널에 해당하는 것이 이다.
CNN에서 사용하는 연산은 사실 convolution이 아니고,
cross-correlation이라 부른다.
전체 공간에서는 부호에 따라 차이가 없지만, 컴퓨터에서는 차이가 있다. 하지만, 관용적으로 > convolution 연산이라고 부른다.
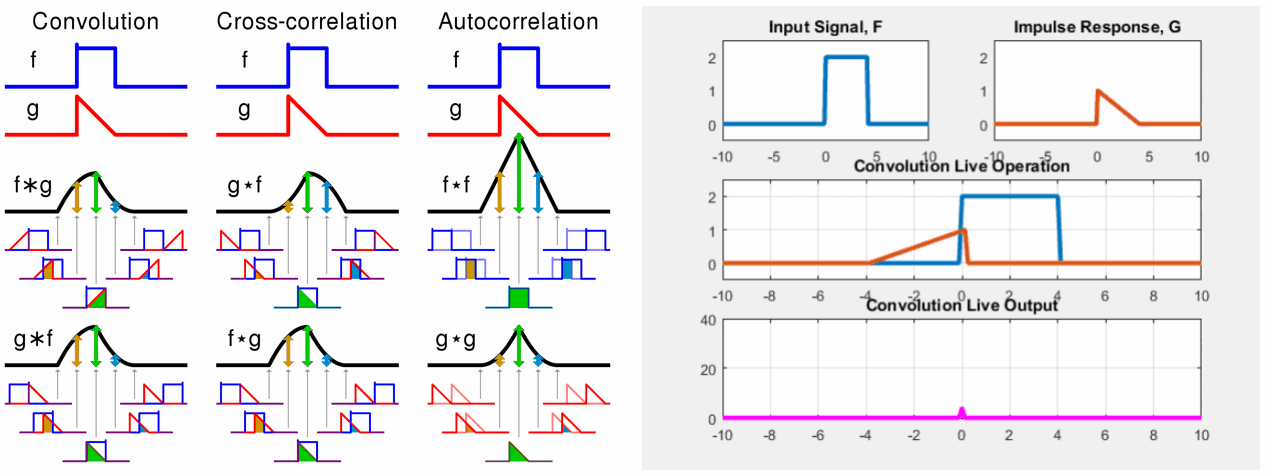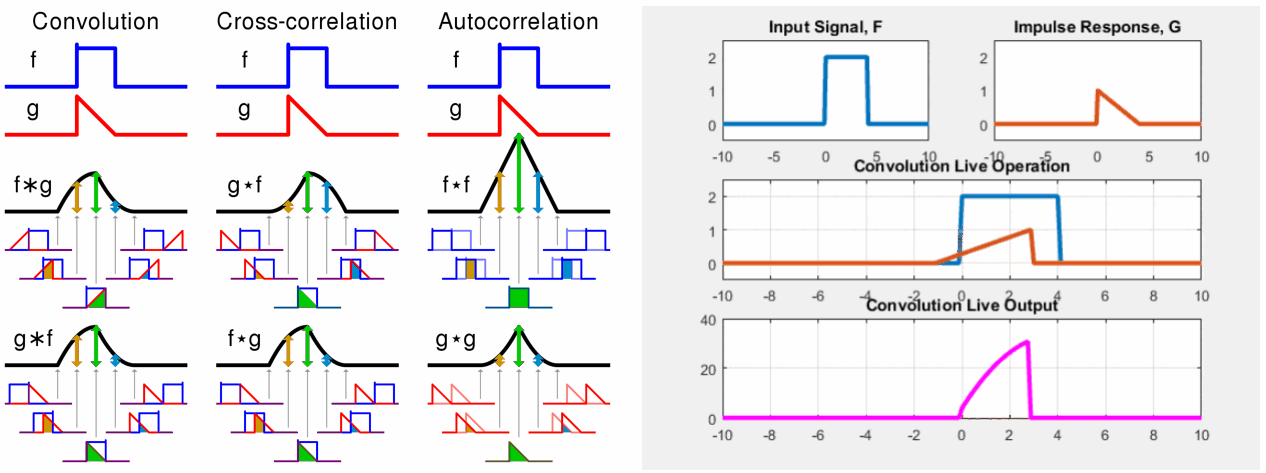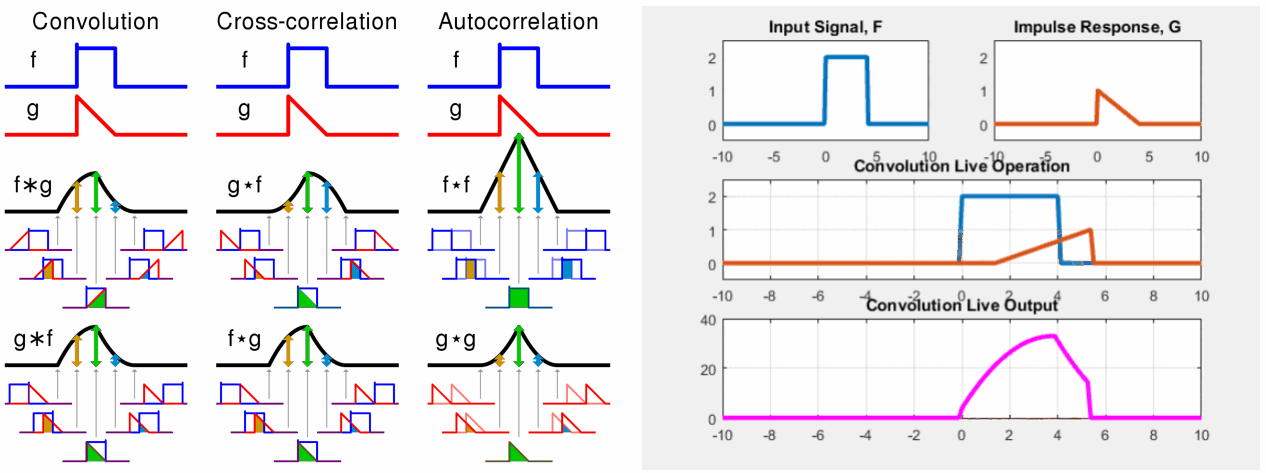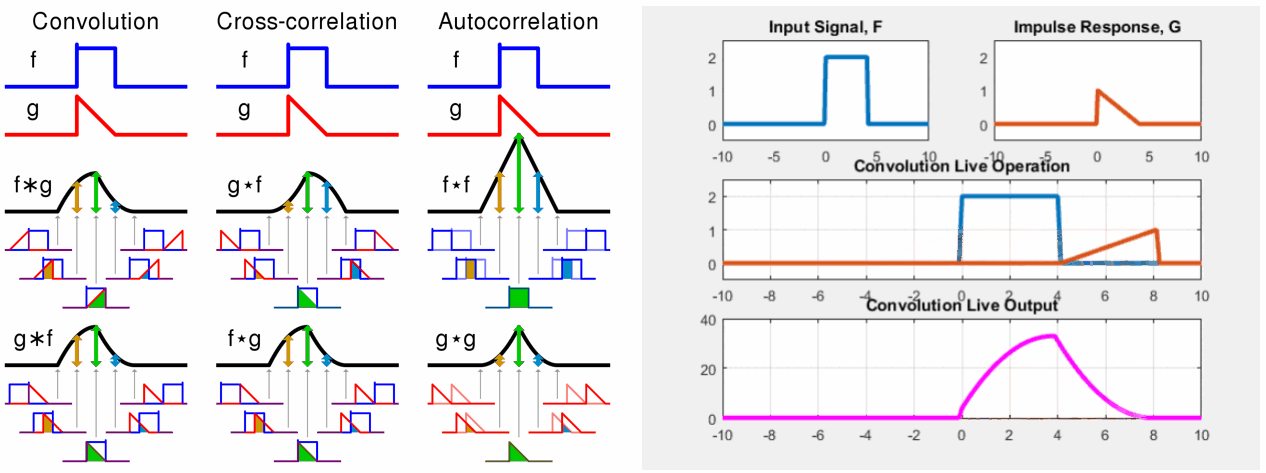
먼저 임의의 변수(dummy variable)를 정의한다. (이 경우에는 를 정의함) 이제 정의한 변수를 축으로 두 함수의 파형을 그린다. 그 다음으로 두 함수 중 하나를 선택해 축에 대해 반전(time-invert)하고 t를 더한다. (어떤 함수를 선택하든지 관계 없다.) 방금 선택한 함수는 -축에 대해 앞뒤로 움직일 수 있다. 이때 t 변수의 값이 변화하지만 위 그림에서 파형의 뾰족한 부분은 항상 t-1에 위치해 있다. 이제는 음의 무한대에서부터 양의 무한대까지 선택한 함수를 이동시키면서 두 함수의 곱의 적분 값을 찾는다. 이 결과를 파형으로 표시한 것이 바로 두 함수의 합성곱이다.
- 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용한다.
2. 다차원 convolution
1D-conv:
2D-conv:
3D-conv:
-
데이터의 성격에 따라 사용하는 커널의 차원이 달라진다.
-
음성인 경우 1D-conv, 흑백 사진인 경우 2D-conv, 컬러 사진인 경우 3D-conv를 사용한다.
-
가 바뀌어도 커널 의 값은 바뀌지 않는다.
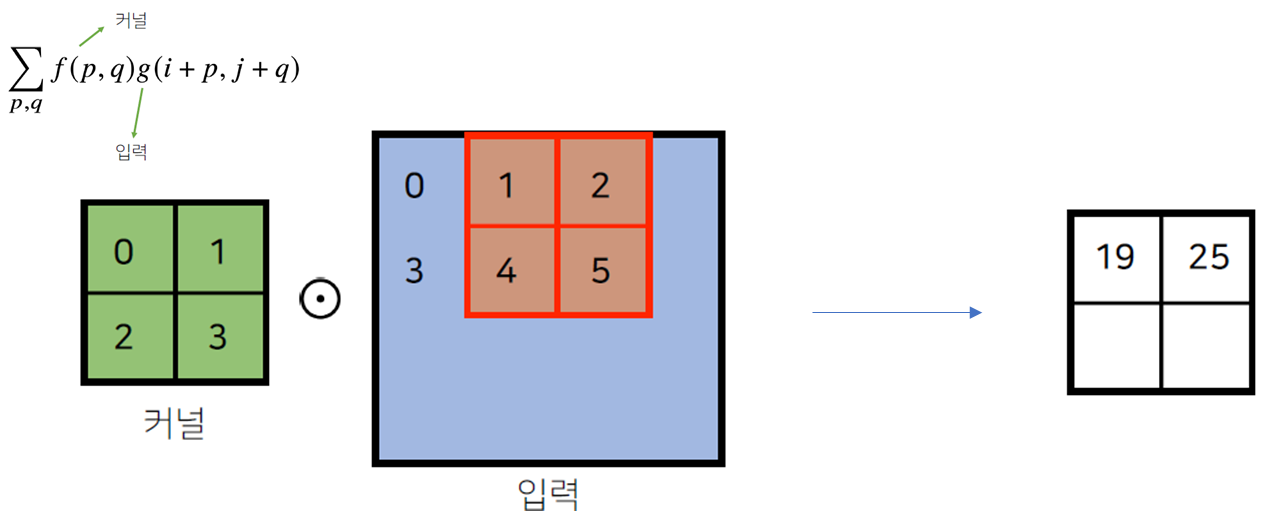
2.1. 2D-Conv
-
2D-Conv 연산은 커널을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다.
-
입력 크기를 , 커널 크기를 , 출력 크기를 라고 하면, 출력크기는 다음과 같이 계산한다.
- 예를들어 28×28입력을 3×3커널로 2D-conv 연산하면, 출력 사이즈는 26×26이 된다.
import numpy as np
def conv2D(arr, kernel):
arr_row, arr_col = len(arr), len(arr[0])
kernel_row, kernel_col = len(kernel), len(kernel[0])
ret_row = arr_row - kernel_row + 1
ret_col = arr_col - kernel_col + 1
ret = np.zeros([ret_row, ret_col], dtype = int)
for r in range(ret_row):
for c in range(ret_col):
hadamard_product = kernel * arr[r:r+kernel_row, c:c+kernel_col]
sum_ = np.sum(a=hadamard_product)
ret[r][c] = sum_
return ret
X = np.array([
[1, 0, 1, -1],
[0, 1, 0, 0],
[1, 1, 0, -1],
[-1, -1, 1, 1],
])
K = np.array([
[1, 2],
[3, 4],
])
Y = conv2D(X, K)
print(Y)
2.2. 3D-Conv
-
3D-Conv는 채널이 여러 개인 2D-Conv 연산이다.
-
채널이 여러 개인 2차원 입력의 경우 2차원 convolution을 채널 개수만큼 커널을 만들고, 각 채널에 적용한다고 생각하면 된다.
-
3차원부터는 행렬이 아닌 텐서라 부른다.

-
텐서를 직육면체 블록으로 이해하면 좀 더 이해하기 쉽다.
-
커널을 개 사용하면, 출력도 텐서가 된다.
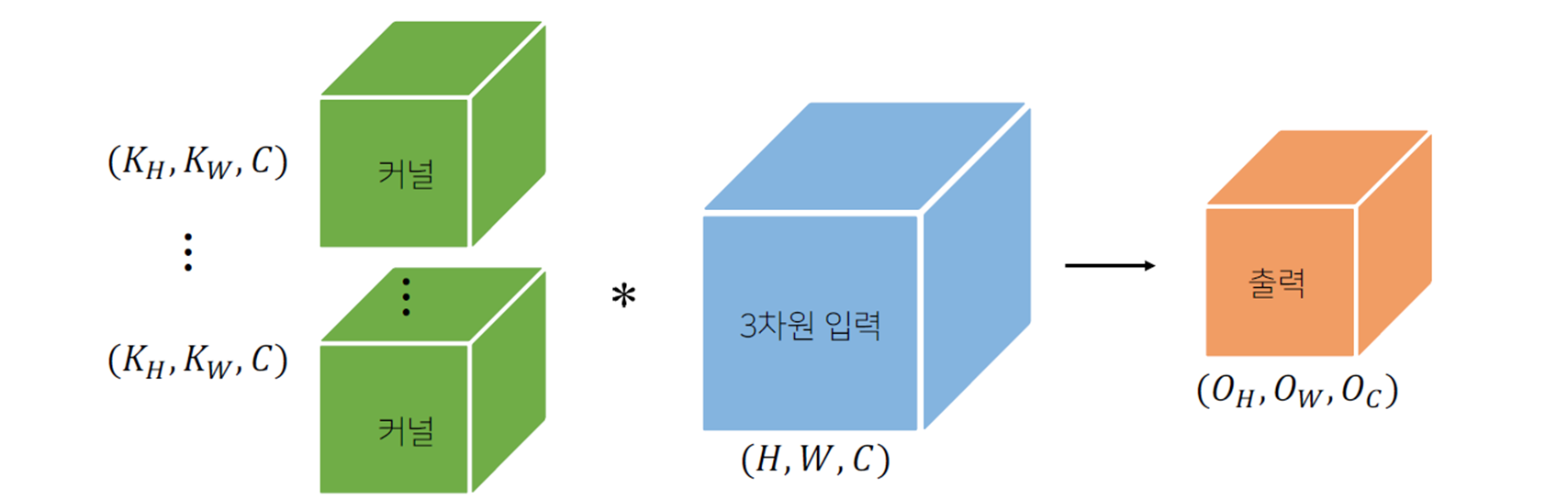
- 위의 기본적인 convolution을 바탕으로, 다양한 변형된 convolution이 존재한다.
3. Convolution 연산의 역전파
- Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에, 역전파를 계산할 때 convolution 연산이 나오게 된다. 즉, 미분을 해도 convolution 연산이 나온다.
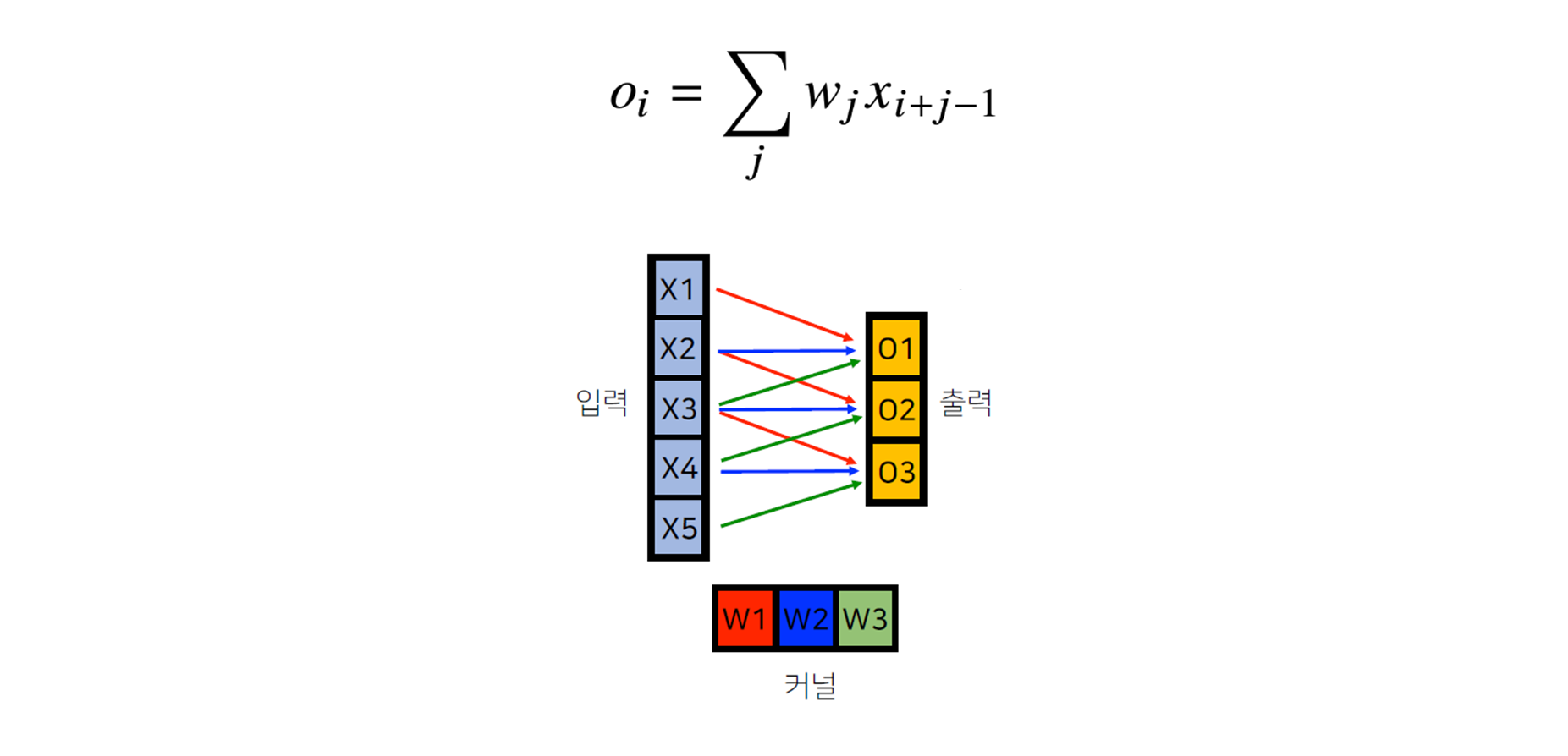
- 그림으로 이해하면 더 쉽다.
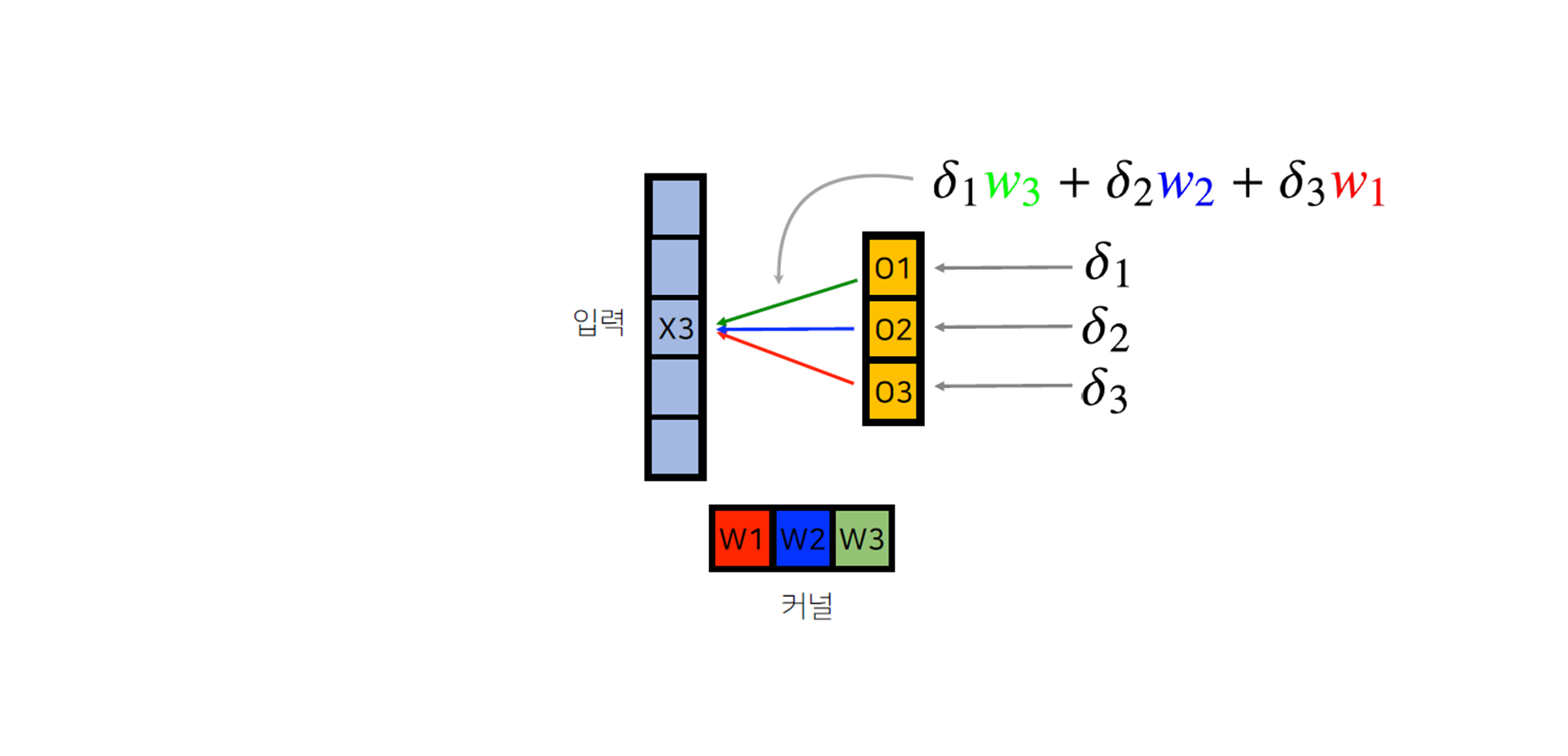
-
각 는 loss의 미분값을 의미한다.
-
역전파 단계에서 다시 커널을 통해 그레디언트가 전달된다.
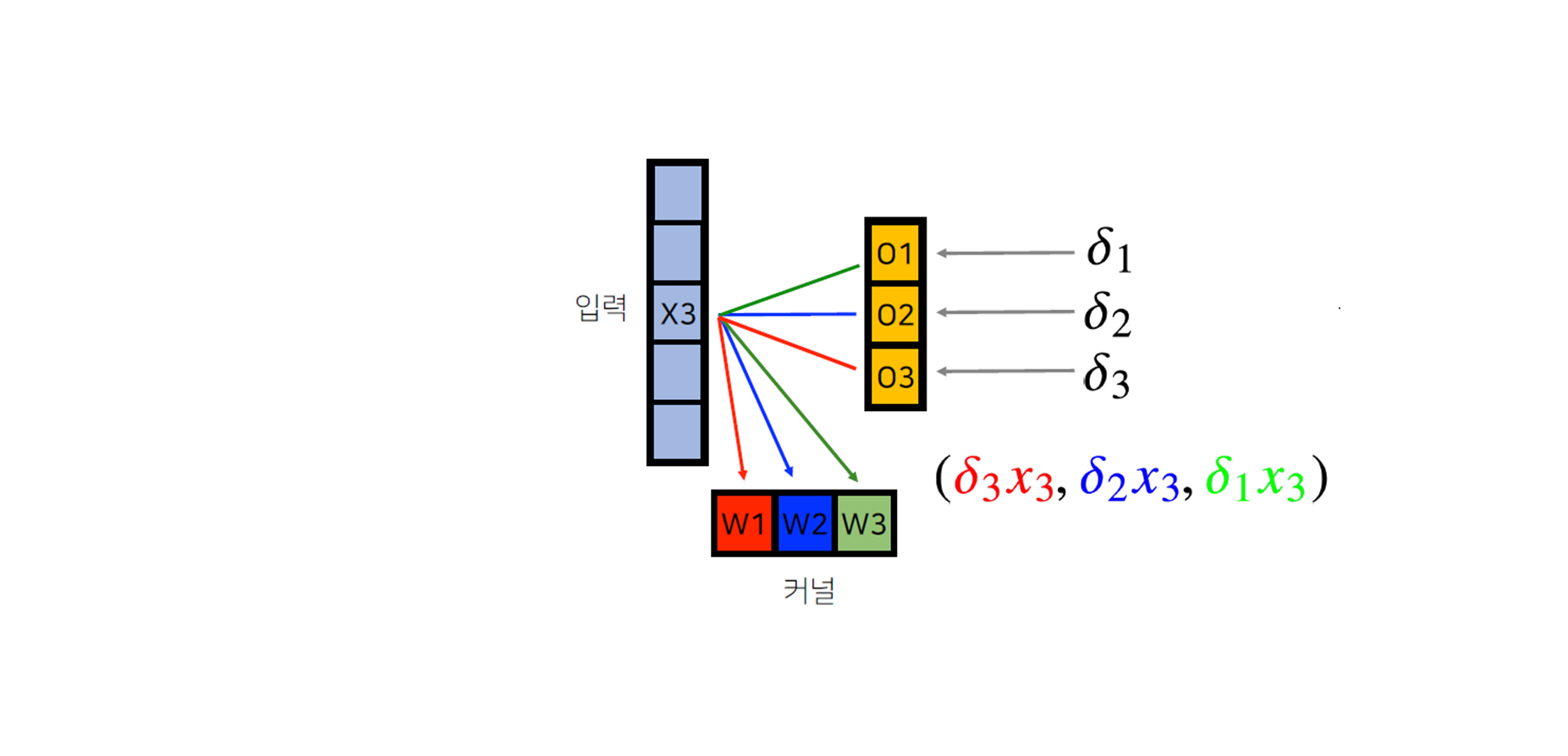
- 커널에는 에 입력값 을 곱해서 전달한다.
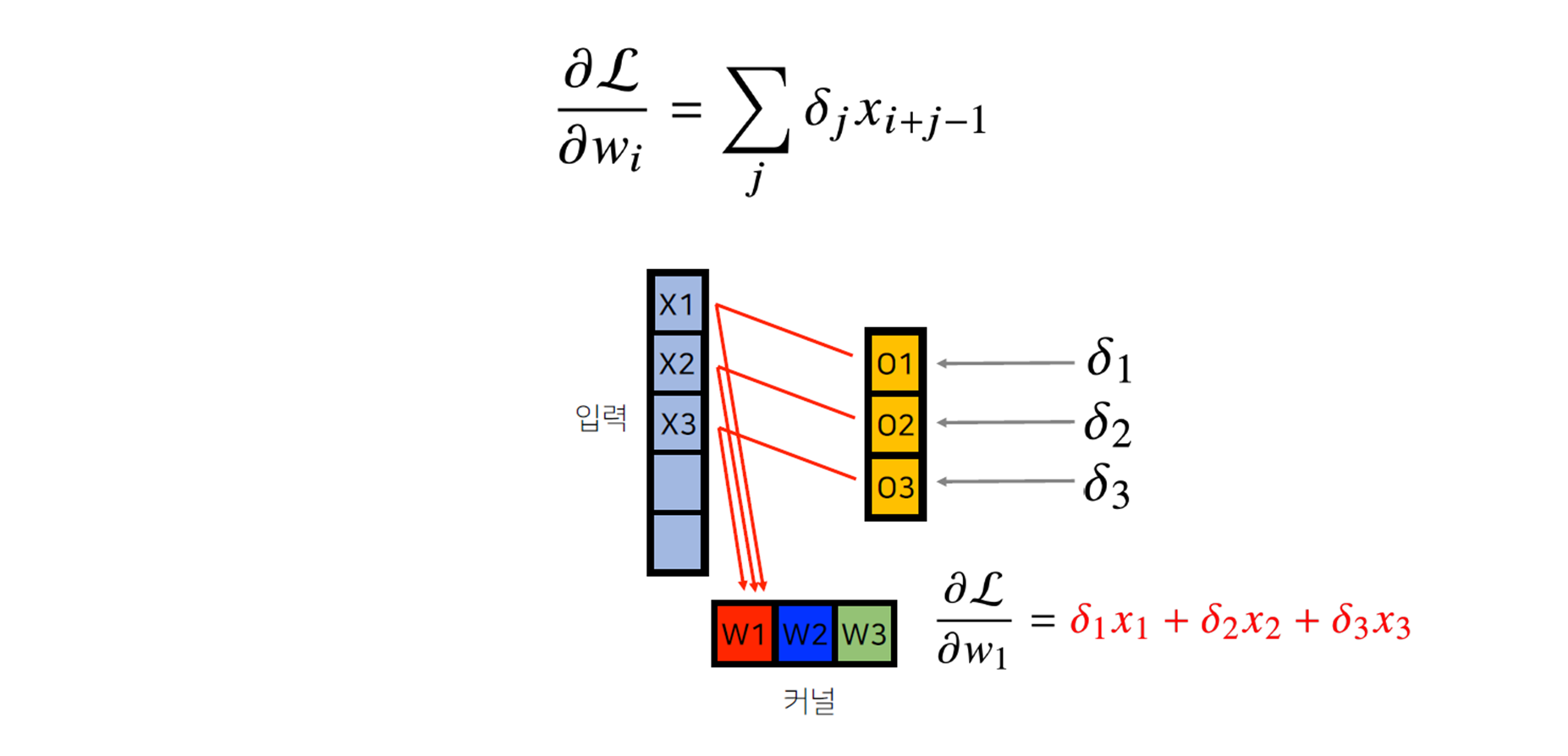
- 각 커널에 들어오는 모든 그레디언트를 더하면, 결국 convolution 연산과 같다.