노름(norm)과 행렬

1. 노름(norm)

---

• 벡터의 노름은 원점에서부터의 거리를 말한다. 기호는 $||vector||$이다.

• 노름의 중류는 $L_0, L_1, L_2, \cdots, L_{\infin}$ 등 다양한 종류가 있다.

• 노름은 임의의 차원 d에 대해 성립하고, 차원에 따라 기하학적 성질이 달리진다.

• 머신러닝에선 목적에 따라 각 성질들이 필요할 때가 있으므로 둘 다 사용한다.

• $L_p$는 다음과 같이 정의한다. $||x||_p = \sqrt[p]{\sum\limits_i|x_i|^p}$ where $p \in R$

1.1. $L_1$ 노름

• Taxical norm, 다른 이름은 맨해튼 노름(Manhattan norm)으로, 다음과 같이 정의한다.

• $L_1$ 노름은 각 성분의 변화량의 절대값을 모두 더한다.

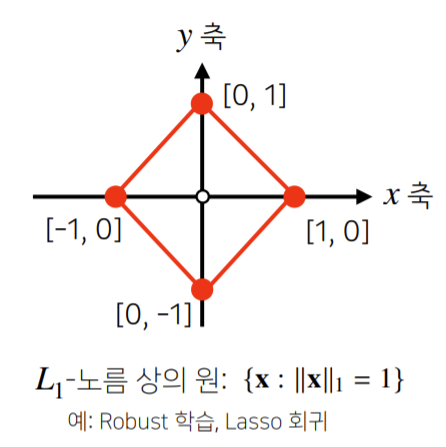
1.2. $L_2$ 노름

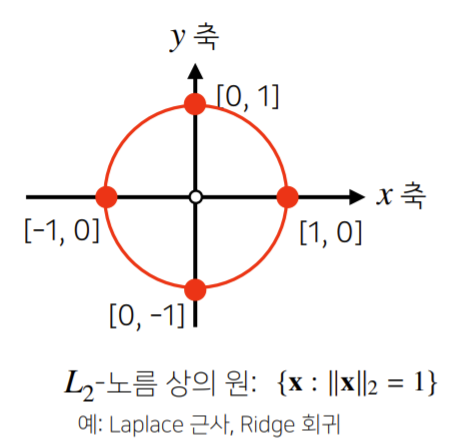
• 유클리드 노름(Euclidean norm)이라고 부르고 다음과 같이 정의한다.

• $L_2$ 노름은 피타고라스 정리를 이용해 유클리드 거리를 계산한다.

1.3. 두 벡터 사이의 거리, 각도

• 벡터에서 거리를 구하는 방법으로는 L1 노름, L2 노름 등이 있다. 각 노름에 따라 값이 달라진다.

• ex) $||x-y||_p$

• 두 벡터 사이의 거리(L2 노름만 사용)를 이용해 각도를 사용한다. 각도를 내적(inner product)과 제2 코사인법칙을 활용한다.

• 내적은 정사영(orthogonal projection)된 벡터의 길이와 관련 있다.

• 정사영된 길이는 제2 코사인법칙에 의해 $||x||cos(θ)$가 된다.

• 내적은 정사영의 길이를 벡터 y의 길이 ||y||만큼 조정한 값이다. - $Proj_y(x)$

• 내적은 두 벡터의 유사도(similarity)를 측정하는데 사용 가능하다.

#!/usr/bin/python
import numpy as np
x = np.array([1, 7, 2])
y = np.array([5, 2, 1])
# 덧셈
print(x + y) # [6 9 3]
# 뺄셈
print(x - y) # [-4  5  1]
# 성분곱
print(x * y) # [ 5 14  2]

# 노름1
def l1_norm(x):
    x_norm = np.abs(x)
    x_norm = np.sum(x_norm)
    return x_norm
    
# 노름2
def l2_norm(x):
    # L2 노름은 np.linalg.norm을 이용해도 구현 가능.
    x_norm = x*x
    x_norm = np.sum(x_norm)
    x_norm = np.sqrt(x_norm)
    return x_norm

# 각도
def angle(x, y):
    v = np.inner(x, y) / (l2_norm(x) * l2_norm(y))
    theta = np.arccos(v)
    return theta

2. 행렬과 역행렬

---

2.1. 행렬(matrix)이란?

• 행렬은 벡터를 원소로 가지는 2차원 배열이다.

• 행렬은 주로 대문자 볼드체, 벡터는 소문자 볼드체로 표기한다.

• 벡터는 index가 하나였지만, 행렬은 행과 열이라는 index를 가진다.

• 행렬끼리 같은 모양을 가지면 덧셈, 뺄셈, 성분곱 연산을 할 수 있다. 벡터에서의 덧셈, 뺄셈, 성분곱 연산과 똑같다.

• 두 행렬의 곱셈은 i 번째 행벡터와 j 번째 열벡터 사이의 내적을 성분으로 가지는 행렬이다.

• 넘파이의 np.inner는 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다. → 수학에서 말하는 내적과 다르다.

#!/usr/bin/python
import numpy as np
X = np.array([[1, -2, 3],
              [7, 5, 0],
              [-2, -1, 2]])


Y = np.array([[0, 1, 2],
              [1, -1, 0],
              [-2, 1, -3]])
              
print(X + Y) # 덧셈
print(X - Y) # 뺄셈
print(X * Y) # 성분곱
print(X @ Y) # 곱셈
print(np.inner(X,Y))

# 결과
# [[ 1 -1  5]
#  [ 8  4  0]
#  [-4  0 -1]]
#
# [[ 1 -3  1]
#  [ 6  6  0]
#  [ 0 -2  5]]
#
# [[ 0 -2  6]
#  [ 7 -5  0]
#  [ 4 -1 -6]]
#
# [[ -8   6  -7]
#  [  5   2  14]
#  [ -5   1 -10]]
#
# [[  4   3 -13]
#  [  5   2  -9]
#  [  3  -1  -3]]

2.2. 전치행렬(transpose matrix)이란?

• 행과 열의 인텍스가 바뀐 행렬.

2.3. 행렬을 이해하는 방법

2.3.1. 데이터

• 벡터가 공간에서 한 점을 의미한다면, 행렬은 여러 점들을 나타낸다.
• 행렬의 행벡터 xi는 i번째 데이터를 의미한다.

2.3.2. 연산자

• 행렬을 이용한 연산자를 linear transform이라고 부른다.
• 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.
• 행렬곱을 통해 패턴을 추출할 수 있고, 데이터를 압축할 수도 있다.

2.4. 역행렬이란?

• 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)라고 부른다.

• 역행렬이 존재하려면 square matrix이면서, 행렬식(determinant)이 0이 아니어야 한다. 즉, full rank이어야 한다.

• 어떤 행렬과 그 행렬의 역행렬을 곱하면 항등행렬이 된다.

• 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬을 이용한다.

• 행(m)과 열(n)의 크기에 따라 유사역행렬을 구하는 방법이 2가지로 나뉜다.

• 행이 열보다 많을 경우(m >= n), 유사역행렬은 행렬보다 먼저 곱해져야 항등행렬이 된다.

$m \ge n$ 인 경우 $\boldsymbol{A}^+ = (\boldsymbol{A}^T\boldsymbol{A})^{-1}\boldsymbol{A}^T$
$n \ge m$ 인 경우 $\boldsymbol{A}^+ = \boldsymbol{A}^T(\boldsymbol{A}^T\boldsymbol{A})^{-1}$

$m \ge n$이면 $\boldsymbol{A}^+ \boldsymbol{A}= \boldsymbol{I}$가 성립.
$n \ge m$이면 $\boldsymbol{A} \boldsymbol{A}^+= \boldsymbol{I}$만 성립.

#!/usr/bin/python
import numpy as np
X = np.array([[1, -2, 3],
              [7, 5, 0],
              [-2, -1, 2]])


# 역행렬은 numpy.linalg.inv로 구할 수 있다.
inv_X = np.linalg.inv(X)
print(inv_X)
print(X@inv_X)

# 결과
# [[ 0.21276596  0.0212766  -0.31914894]
#  [-0.29787234  0.17021277  0.44680851]
#  [ 0.06382979  0.10638298  0.40425532]]
#
# [[ 1.00000000e+00  0.00000000e+00  0.00000000e+00]
#  [-2.22044605e-16  1.00000000e+00  0.00000000e+00]
#  [-2.77555756e-17  0.00000000e+00  1.00000000e+00]]


Y = np.array([[0, 1],
              [1, -1],
              [-2, 1]])
              
# 유사역행렬은 numpy.linalg.pinv로 구할 수 있다.              
pinv_Y = np.linalg.pinv(Y)
print(pinv_Y)
print(pinv_Y@Y)

# 결과
# [[ 5.00000000e-01  8.32667268e-17 -5.00000000e-01]
#  [ 8.33333333e-01 -3.33333333e-01 -1.66666667e-01]]
#
# [[ 1.00000000e+00 -2.22044605e-16]
#  [ 0.00000000e+00  1.00000000e+00]]

2.5. 응용1: 연립방정식

• n >= m일 때, 즉 해(solution)가 무수히 많을 때, 유사역행렬을 이용해 많은 해 중 하나를 구할 수 있다.

2.6. 응용2: 선형회귀분석

• m >= n일 때, 즉 해가 존재하지 않을 가능성이 많을 때, 유사역행렬을 이용해 최적의 해(best solution)을 구할 수 있다.

• 최적의 해(best solution)란, L2을 최소화 하는 것으로, 많은 데이터를 가장 잘 표현할 수 있는 선형회귀 모델을 구하는 것과 유사하다.

• Moore-Penrose 역행렬을 이용하면 y에 근접하는 y-hat을 찾을 수 있다.

• sklearn의 LinearRegression은 Moore-Penrose를 이용한 것이다.

Reference

---

• 기본 마크다운 문법
• 노름(norm)