SW사관학교 정글7기 개발일지 (08/13)

python

yield로 permutaions, combinations 구현하기

itertools를 사용하다 보니 순열, 조합 관련 알고리즘을 직접 구현할 수 있는 능력의 필요성을 느꼈습니다.

itertools의 permutations, combinations를 공부하면서 알게된 yield를 활용해보기로 했습니다.

재귀형태를 뛰고있어서 어떻게 generate()의 결과값을 permutation()밖으로 끄집어낼지 찾아보다가 yield from 을 알게되어 활용했습니다.

import time


def permutation(arr, r):
    arr = sorted(arr)
    used = [False for _ in range(len(arr))]

    def generate(chosen):
        if len(chosen) == r:
            time.sleep(1)
            yield chosen

        for i in range(len(arr)):
            if not used[i]:
                used[i] = True
                chosen.append(arr[i])
                yield from generate(chosen)
                used[i] = False
                chosen.pop()

    yield from generate([])


def combination(arr, r):
    arr = sorted(arr)

    def generate(chosen, start):
        if len(chosen) == r:
            time.sleep(1)
            yield chosen

        for i in range(start, len(arr)):
            if arr[i] not in chosen:
                chosen.append(arr[i])
                yield from generate(chosen, i+1)
                chosen.pop()

    yield from generate([], 0)


test = ['A','B','C']

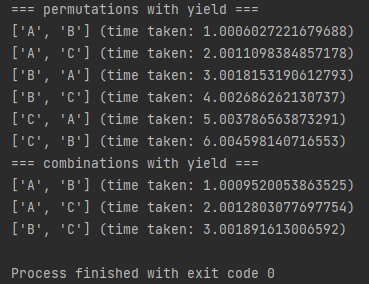
print('=== permutations with yield ===')
start = time.time()
for p in permutation(test, 2):
    print('{} (time taken: {})'.format(p, time.time() - start))

print('=== combinations with yield ===')
start = time.time()
for c in combination(test, 2):
    print('{} (time taken: {})'.format(c, time.time() - start))

실행결과

---

baekjoon

외판원 순환2

N = int(input())
cost = [list(map(int, input().split())) for _ in range(N)]


def find(visited, now):
    if (visited << N) | now in dp:
        return dp[(visited << N) | now]
    if visited == (1 << N) - 1:
        return cost[now][0] if cost[now][0] > 0 else 10 ** 9

    tmp = 10 ** 8
    for i in range(1, N):
        if not visited & (1 << i) and cost[now][i]:
            tmp = min(tmp, find(visited | (1 << i), i) + cost[now][i])

    dp[visited << N | now] = tmp
    return tmp


# key: visited << N | now, value: cost
dp = {}

# visited: bit로 표현된 방문한 도시 ex) 0b1000 4개 중 첫번째 도시만 방문함
print(find(1, 0))

정말 예술적인 코드를 발견해서 조금 수정해서 적용해봤다.

---

연산자 끼워넣기

def f(result, idx, a, b, c, d):
    global N, nums, maximum, minimum
    if idx == N:
        if result > maximum:
            maximum = result
        if result < minimum:
            minimum = result

    if a:
        f(result + nums[idx], idx+1,  a-1, b, c, d)
    if b:
        f(result - nums[idx], idx+1, a, b-1, c, d)
    if c:
        f(result * nums[idx], idx+1, a, b, c-1, d)
    if d:
        f(int(result / nums[idx]), idx+1, a, b, c, d-1)


N = int(input())
nums = [*map(int, input().split(' '))]
a, b, c, d = map(int, input().split(' '))

maximum = -10**9
minimum = 10**9

f(nums[0], 1, a, b, c, d)
print(f'{maximum}\n{minimum}')

원본 코드

이것도 놀라워서 원본코드를 참고해서 조금 수정해봤다.