백준 문제 풀이
9663 N-Queen
이전에 놓은 queens와 충돌하는지 판단하는 방법 -> y = |x| 그래프에 대응하는지 판단
- row의 차이와 |col의 차이|가 같을 경우 충돌한다고 판단.
메인 코드
n = int(input())
# indexing 값을 row로 입력하면 col을 나타낸다.
# 해당 좌표에는 queen이 있음
col = [-1 for _ in range(n)]
cnt = 0 # 배치한 queen의 개수
# 현재 확인중인 row에 놓은 queen이 이전 row들의 queen과 충돌하는지 확인하는 함수
def is_valid_position(row):
for r in range(row):
if col[r] == col[row] or \
row - r == abs(col[row] - col[r]):
return False
return True
def n_queen(row: int):
global cnt
if row == n:
cnt += 1
return
for c in range(n):
col[row] = c
if is_valid_position(row):
n_queen(row + 1)
n_queen(0)
print(cnt)후기
column을 list로 표현해서 col[row]형태로 사용하는게 놀라워서 적용해봤다.
처음엔 y = x, y = -x 그래프를 그려서 대응하는 방식을 사용했는데, 절댓값을 사용하면 쉽게 계산할 수 있었다.
현재 queen좌표와 충돌하는지 판단하는 queen 사이의 직선을 직각이등변 삼각형의 빗변 이라고 생각하면 가로 길이 == 세로길이 -> 대각선 상에 있음
을 판단할 수 있다.
2805 나무자르기

나무를 자를 수 있는 높이의 범위가 너무 넓다.
-> 중간값을 테스트 해가면서 성공하는 범위, 실패하는 범위를 찾는다.
-> 결정 구간이 나뉘어지는 경계선 (이 경우는 ~T / F~ 구간)을 찾아서 lo를 반환하자!
# 잘라도 되는 높이인지 판단하는 함수
def good_to_go(cut_height) -> bool:
global woods, M
total = 0
for w in woods:
if w > cut_height:
total += w - cut_height
return total >= M
N, M = map(int, input().split(' '))
woods = [*map(int, input().split())]
# 이진 탐색 수행, lower_bound 활용
lo = 0
hi = 10**9 + 1
while lo + 1 < hi:
mid = (lo + hi) // 2
# lo에 T구간에 해당하는 mid를 집어넣는다. -> lower_bound 활용
# 이는 가능한 값 중 최솟값을 찾는다는 문제 내용에서 유추 가능함.
if good_to_go(mid):
lo = mid
else:
hi = mid
print(lo)
후기
바로 아래에 작성한 binary search에 표기했지만
'백준 이진탐색 헷갈리지 않고 구현하기' 내용이 도움이 많이됏다.
알고리즘
binary search 이진 탐색
정렬 된 데이터 중 탐색할 영역을 반으로 쪼개 왼쪽, 오른쪽을 판단하며 탐색하는 방법
시간복잡도는 O(logN)이다. 밑수는 2
구현 Checklist
- 탐색할 array에서
~T / F~또는~F / T~결정 구간을 정한다. - 결정 구간의 경계선이 lo, hi 사이에 있도록 위치한다.
- mid가 True or False 인지에 따라서 lo에 저장할지, hi에 저장할지 결정한다.
- ex)
~T / F~로 결정구간을 정했다.
if) mid가T(True)구간이다! -> lo = mid
if) mid가F(False)구간이다! -> lo = hi
- while 조건: lo + 1 < hi
- 탐색에 성공했을 때 lo가 답일지, hi가 답일지 잘 정해야한다.
- 결정 구간에 따라 달라진다.
- lo, hi의 초기값 잘 설정했는지 확인한다.
ex) 결정구간~T / F~, 초기값 lo = 3 인데 인덱스 2부터 모두 False일 경우 -> 최소한 최소값이 2보다 작아야 한다.
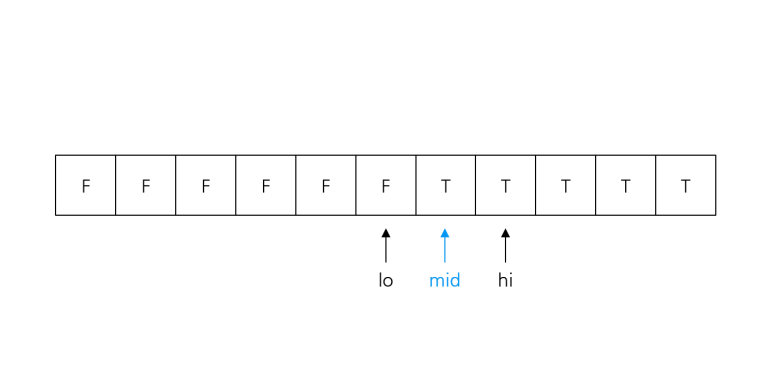 탈출전 마지막 loop에서의 상태
탈출전 마지막 loop에서의 상태
사용한 예시: 백준 2805 나무자르기

