온라인 Forecasting 교재 [Forecasting : Principles and Practice] 8장을 참고하여 작성하였습니다.

8. ARIMA 모델

• 시계열 예측 방법 중 exponential smoothing과 함께 가장 널리 사용하는 방식
• 데이터에 나타나는 자기상관(autocorrelation) 을 표현하기 위해 만들어진 모델이다.
  • exponential smoothing : 추세와 계절성을 표현

8.1 정상성과 차분

8.1.1 정상성(Stationarity)

• 해당 시계열 데이터가 시점과 무관한 특징을 가진다.
  • 추세나 계절성이 존재 → 정상성 X
  • 백색잡음인 시계열 데이터 → 정상성 O
  • 주기 O (추세 X, 계절성 X) → 정상성 O
    • 주기는 고정된 길이를 가지고 있지 않고, 주기의 고점이나 저점이 어딘지 확실히 알 수 없다.
  • 일반적으로 정상성 O → 예측할 수 있는 패턴 X

ㄟ(▔,▔)ㄏ 
주기는 고정된 길이를 가지고 있지 않고, 
주기의 고점이나 저점이 어딘지 확실히 알 수 없다.

주기는 해당 주기의 길이를 파악할 수 없기 때문에, 시점과 무관하다는 것을 의미하는지?

예시 : 정상성 유무 판단

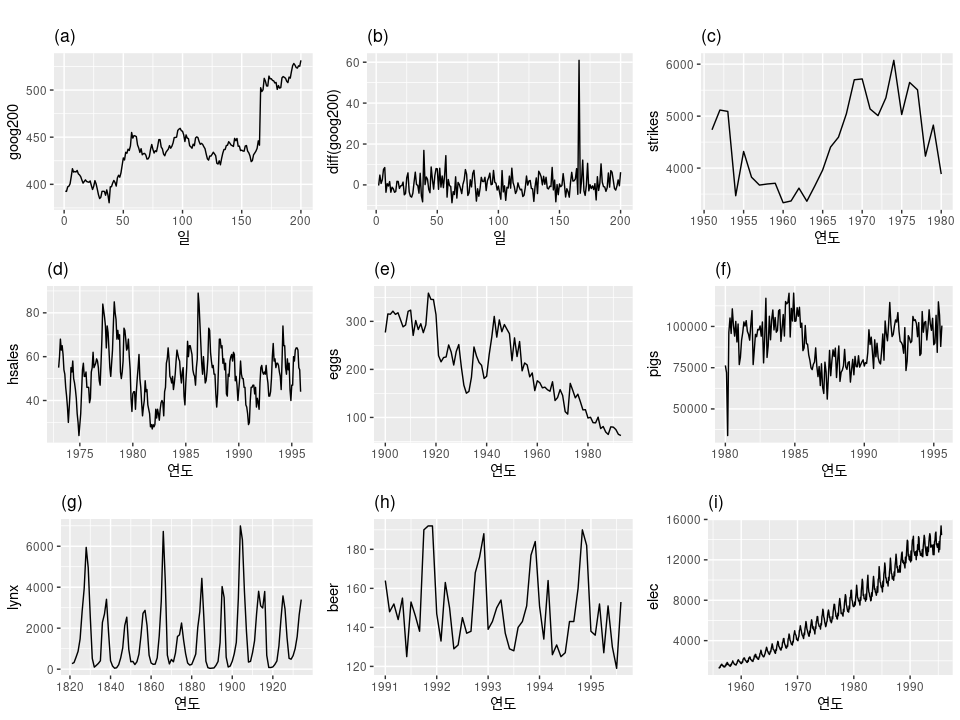
• 계절성이 있는 (d), (h), (i)는 정상성 X
• 추세가 있고 수준이 변하는 (a), (c), (e), (f), (i)

  ㄟ(▔,▔)ㄏ
  (c)와 (f)는 추세가 있다고 할 수 있나?
  수준이 변하는 그래프인가?

• 분산이 증가하는 (i)
• (b)는 정상성을 나타낸다.
• (g)는 주기가 존재하여 정상성이 없는 시계열 데이터로 볼 수 있지만, 주기의 불규칙성이 존재하여 주기의 시작이나 끝을 예측할 수 없기 때문에 이 시계열은 정상성을 나타낸다.

8.1.2 차분(differencing)

• 관측값들의 차이를 계산하는 것
• 정상성이 없는 시계열 데이터를 정상성을 나타내게 할 수 있는 방법
  • 위 [예시] 그림에서 (a)는 시계열 데이터, (b)는 시계열 데이터의 일일변동 데이터인데, (a)에서는 정상성이 없었으나, (b)에서는 추세나 수준 변화가 없어지면서 정상성을 나타냄을 알 수 있다.
• ACF 그래프
  
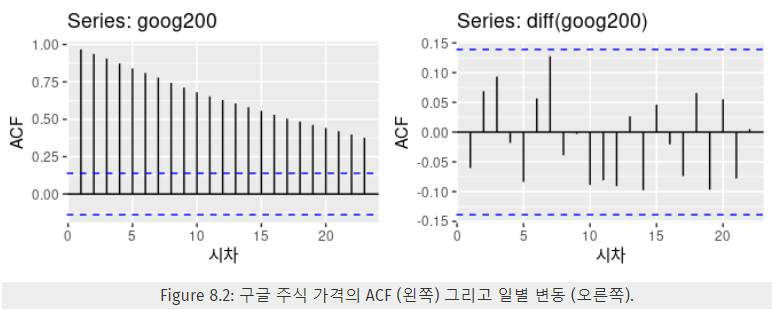
  • 정상성 X → ACF가 느리게 감소, r_1은 종종 큰 양수를 갖는다.
  • 차분의 ACF를 보면 95% 한계 바깥에 자기상관 값이 없기 때문에 단순히 백색잡음 시계열처럼 보인다. → 일일 변동이 기본적으로 이전 거래일의 데이터와 관련이 없는 값임을 나타낸다. → 정상성 O

8.1.3 확률보행 모델(random walk model)

• 차분 y_t' (관측값의 차이)
  $y_t' = y_t - y_{t-1}$
• 첫 번째 관측값에 대한 차분 y_1'을 계산할 수 없기 때문에
  T-1 개의 차분만을 가진다.
• 백색잡음 데이터의 차분을 구할 때,
  $y_t - y_{t-1} = ε_t$
  로 표현할 수 있고, 여기서 ε_t는 백색잡음을 의미한다.
• 이를 정리하면 "확률보행 모델" 을 얻을 수 있다.
  $y_t = y_{t-1} + ε_t$

8.1.4 2차 차분

• 차분을 구했을 때도 정상성이 없을 수 있는데, 이 때 차분의 차분을 구하면서 정상성을 나타내는 시계열 데이터를 얻을 수 있다.
  $y_t'' = y_t' -y_{t-1}''$
  $= (y_t - y_{t-1}) - (y_{t-1}-y_{t-2})$
  $= y_t - 2y_{t-1}+y_{t-2}$
• T-2 개의 차분만을 가진다.
• "변화에서 나타나는 변화"를 모델링하게 되는 것인데, 실제로는 2차 차분 이사응로 구하는 경우는 거의 없다.

8.1.5 계절성 차분

• 이전 계절의 관측치와의 차이
• m이 계절의 개수라 할 때,
  $y_t' = y_t - y_{y-m}$
• 시차 m차분 이라고도 한다.
• 계절성 차분 데이터가 백색잡음처럼 보인다면, 아래와 같은 식으로 표현할 수 있다.
  $y_t = y_{t-m} + ε_t$
• 이 모델을 통해 구한 예측값은 같은 계절의 마지막 관측값과 같다.

계절성 차분의 2차 차분

• 계절성 차분과 1차 차분을 둘 다 적용할 때,
  • 어떤 것을 먼저 적용해도 큰 차이 X
  • 단, 계절성 패턴이 강하다? 계절성 차분을 먼저 하면 1차 차분을 안 해도 되는 경우가 있다.

1차 차분? 2차 차분? 계절성 차분?

• 어떤 차분을 구할지는 주관적인 요소가 필요하다.
• 모델링 과정에서 항상 몇 가지 선택이 존재하고 분석하는 사람마다 다른 선택을 할 수 있다.
• 이 외의 다른 시차값은 사용하지 않는 것이 좋다. (직관적 해석 불가)

8.1.6 단위근검정

• 차분을 구하는 것이 필요할지에 대한 객관적인 방법
• 검정 방법은 다양하고, 서로 다른 가정에 기초하기 때문에 상반되는 답을 낼 수 있다.

퀴아트코프스키-필립스-슈미트-신 검정 (KPSS)

• Kwiatkowski-Phillips-Schmidt-Shin 검정
• 귀무가설 : 이 검정은 데이터에 정상성이 나타난다.
• 귀무가설이 거짓이라는 증거를 찾음으로써 (== p value < 0.05) 데이터가 정상성을 보이지 않음을 증명한다.

8.2 후방이동 기호(Backshift)

• 시계열의 시차를 다룰 때 유용한 연산자 B
• 시차(lag)를 나타내어 L 이라고도 표현한다.
  $By_t=y_{t-1}$
• 데이터를 한 시점 뒤로 옮기는 역할을 한다.
• 두 시점 뒤로 옮길 때는 아래와 같이 표현한다.
  $B(By_t) = B^2y_t = y_{t-2}$
• 월별 데이터에서 "지난해 같은 달"을 표현할 때는 아래와 같이 표현한다.
  $B^{12}y_t=y_{t-12}$

차분을 구하는 과정에서 후방이동 기호의 사용

• 1차 차분
  $y'_t=y_t-y_{t-1}=y_t-By_t = (1-B)y_t$
• 2차 차분
  $y''_t=y_t-2y_{t-1}+y_{t-2}=(1-2B+B^2)y_t = (1-B)^2y_t$
• d차 차분 $(1-B)^dy_t$
• 차분을 연산자로 결합했을 때 대수의 법칙을 적용할 수 있다.
  • 예시
    $(1-B)(1-B^m)y_t=(1-B-B^m+B^{m+1})y_t$
    $=y_t-y_{t-1}-y_{t-m}+y_{t-m-1}$

8.3 자기회귀 모델(AutoRegressive Model)

• 자기 자신에 대한 변수의 회귀 모델
• 다중 회귀 모델에서는
  목표 예상 변수 x의 선형 조합을 이용하여 관심 있는 변수 y를 예측한다.
• 자기회귀 모델에서는
  과거 관측치의 선형 조합을 이용하여 관심 있는 변수를 예측한다.
• y_t의 시차 값을 예측변수로 다룬다!
• 차수 p의 autoregressive model : AR(p) ($ε_t$ : 오차항)
  $y_t = c + ϕ_1y_{t-1} + ϕ_2y_{t-2} + ... + ϕ_py_{t-p} + ε_t$
• autoregressive model은 다양한 종류의 시계열 패턴을 유연하게 다룰 수 있다.

예시

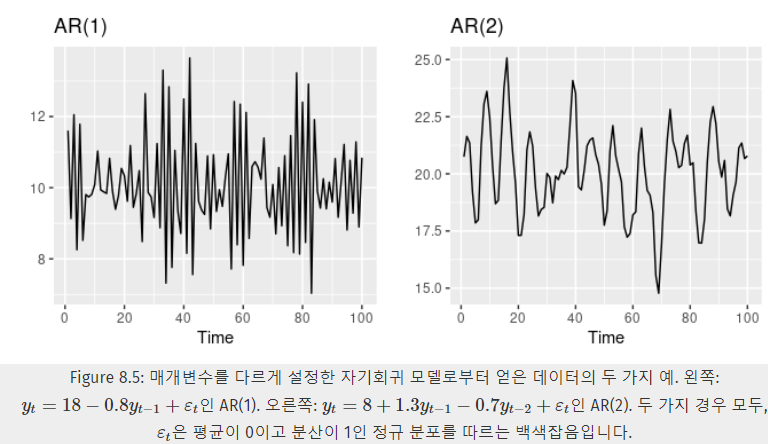
• Figure 8.5는 차수 p가 1일 때와 2일 때 $y_t$를 표현한 것이고,
  $ϕ_1,…,ϕ_p$에 따라서도 시계열 패턴이 달라진다.
  $ε_t$에 따라 눈금이 달라진다.
• AR(1) 모델
  • $ϕ_1 = 0$일 때, $y_t == ε_t$
  • $ϕ_1 = 1$일 때, $c=0$이면, $y_t$는 확률보행 모델
  • $ϕ_1 = 1$일 때, $c≠0$이면, $y_t$는 표류가 있는 확률보행 모델
  • $ϕ_1 < 0$ (음수)일 때, $y_t$는 평균값을 중심으로 진동한다.
• 보통 자기회귀 모델은 정상성이 보이는 데이터에만 사용한다.
  • 이 경우 매개변수 값에 대한 제한조건이 필요하다.
    • AR(1)의 경우 $-1 < ϕ_1 < 1$
    • AR(2)의 경우 $-1 < ϕ_2 < 1,$ $ϕ_1+ϕ_2 < 1,$ $ϕ_2-ϕ_1 < 1$
    • ...

8.4 이동 평균 모델(Moving Average Model)

• AutoRegressive Model에서 과거 값을 사용했다면,
  이동 평균 모델에서는 과거의 예측 오차 ε을 사용한다.
• q차 이동 평균 모델 MA(q)
  $y_t = c + ε_t + ϕ_1ε_{t-1} + ϕ_2ε_{t-2} + ... + ϕ_qε_{t-q}$
• $y_t$ 각 값을 "과거 몇 개의 예측 오차 $ε$의 가중 이동 평균"으로 볼 수 있다.

이동 평균 vs 평활

• 이동 평균 모델은 미래 값을 예측할 때 사용한다.
• 평활은 과거 값의 추세-주기를 측정할 때 사용한다.

예시

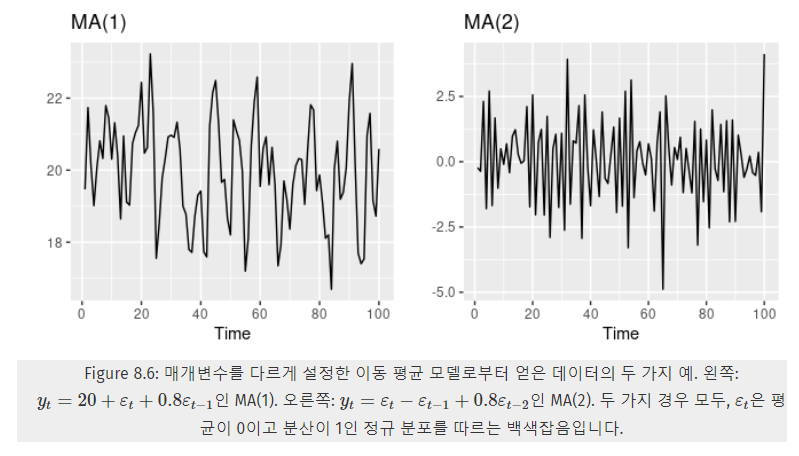
• Figure 8.6는 차수 p가 1일 때와 2일 때 $y_t$를 표현한 것이고,
  $ϕ_1,…,ϕ_p$에 따라서도 시계열 패턴이 달라진다.
  $ε_t$에 따라 눈금이 달라진다.

• 정상성을 나타내는 AR(p) 모델을 MA(∞)로 사용할 수 있다.

  • 예시

    $y_t =ϕ_1y_{t−1}+ε_t$
    $=ϕ_1(ϕ_1y_{t−2}+ε_{t-1})+ε_t$
    $=ϕ_1^2y_{t−2}+ϕ_1ε_{t-1}+ε_{t}$
    $=ϕ_1^3y_{t−3}+ϕ_1^2y_{t−2}+ϕ_1ε_{t-1}+ε_{t}$
    $...$

    • $-1<ϕ_1<1$ 이므로 k가 커질수록 $ϕ_1^k$은 작아진다.

    • 결론적으로 AR(p)모델에서 MA(∞)식을 얻을 수 있다.

      $y_t=ε_t+ϕ_1ε_{t−1}+ϕ^2_1ε_{t−2}+ϕ^3_1ε_{t−3}+...$

• MA 모델은 invertible하다.

  • 즉, MA(q) 모델을 AR(∞)로도 표현할 수 있다.
  • 단, 몇몇의 제한 조건이 필요하다.
    (AutoRegressive model의 정상성 제한 조건과 비슷하다)
    • MA(1)의 경우 $-1 < ϕ_1 < 1$
    • MA(2)의 경우 $-1 < ϕ_2 < 1,$ $ϕ_2+ϕ_1 > -1,$ $ϕ_1-ϕ_2 < 1$
    • ...

  예시 : 왜 $|θ|<1$ 인가?

  • MA(1) : $y_t=e_t+θ_1e_{t−1}$ 를 AR(∞)로 표현하자.

  • 가장 최근의 오차 = 현재와 과거 관측값의 선형 함수

    $e_t = \sum_{j=0}^∞(−θ)^jy_{t−j}$

    ㄟ(▔,▔)ㄏ
    "과거의 모든 관측값의 가중치 곱"은
    과거의 예측값에서 오차를 뺀 값이다.
    
    현재의 오차는
    "현재 예측값"에서 "현재 관측값"의 가중치곱을 뺀 값이다.
    
    근데 위 식을 보면 음수에도 ^j가 포함되어, 
    과거의 모든 관측값의 가중치 곱이 양/음수를 반복하게 되는데, 
    어떻게 식이 성립할 수 있는지 모르겠다.

  • $|θ|>1$이면, 더욱 과거의 관측값일수록 현재 오차에 미치는 영향이 커진다. 🫤

  • $|θ|=1$이면, 가중치가 상수이고, 모든 관측값이 현재 오차에 미치는 영향이 동일하다. 🫤

  • $|θ|<1$이면, 최근 관측값일수록 현재 오차에 미치는 영향이 커진다. 😊

    • MA(1)의 경우 $-1 < ϕ_1 < 1$ 의 제한 조건을 가진다.

8.5 비-계절성 ARIMA 모델

• AutoRegressive Integrated Moving Average : 이동 평균을 누적한 자기회귀
• 차분을 구하는 것을 자기회귀와 이동 평균 모델을 더해서 결합한 것이다.
• $ARIMA(p,d,q)$ 모델
  $y'_t = c+ϕ_1y'_{t−1}+⋯+ϕ_py'_{t−p}+θ_1ε_{t−1}+⋯+θ_qε_{t−q}+ε_t$
  • $p$ : AutoRegressive의 차수
  • $d$ : 차분의 차수(1차 차분, 2차 차분)
  • $q$ : Moving Average의 차수
• AutoRegressive의 정상성과 Moving Average의 가역성은 ARIMA에서 모두 적용된다.

• 후방이동 기호를 사용하면 더 쉽게 표현할 수 있다.
  

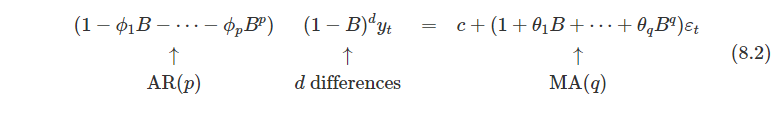
8.5.1 예시 : 미국의 소비 지출

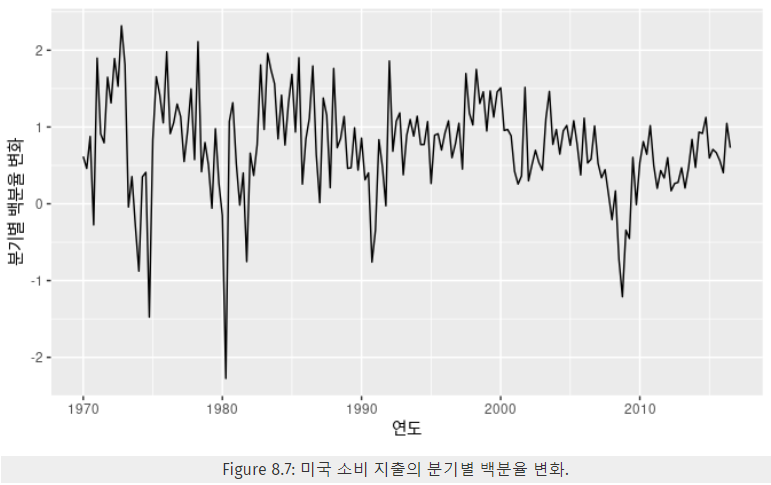
• 아래 Figure 8.7의 시계열 데이터를 ARIMA를 통해 예측해보자.
  
• $ARIMA(1,0,3)$ 모델을 R코드를 통해 실행한 결과,
  
  $y_t=c+0.589y_{t−1}−0.353ε_{t−1}+0.0846ε_{t−2}+0.174ε_{t−3}+ε_t$
  • $c = mean * (1-ar1) = 0.745×(1−0.589)=0.307$
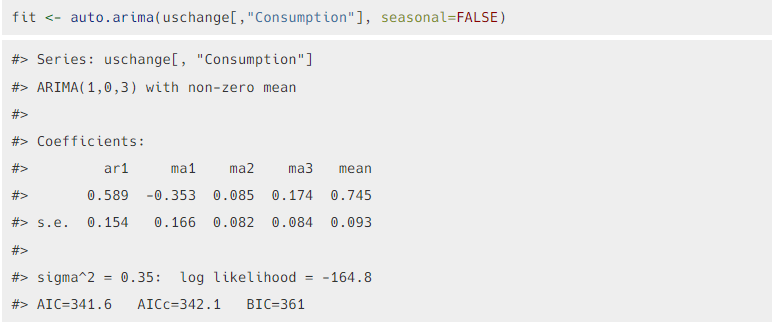
  • $ε_t$는 다음과 같이 $0.592 = \sqrt{0.350}$
    • 이러한 표준편차를 가지는 백색잡음이다.

  ㄟ(▔,▔)ㄏ
  ε_t는 어떤 식에 의해 저렇게 구해지는지?

• 아래 Figure 8.8은 모델로 얻은 예측값이다.
  

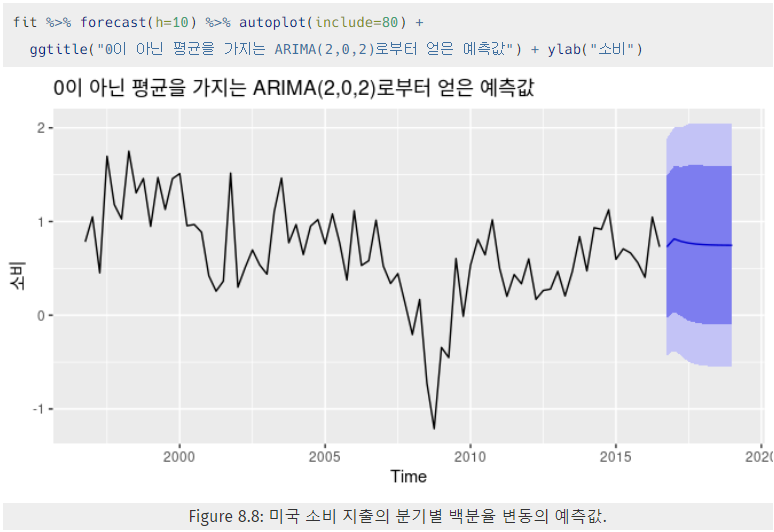
8.5.2 ARIMA 모델 이해하기

: 적절한 $c, d$ 선정

• 상수 c는 장기 예측값에 중요한 영향을 준다.
• 차분의 차수 d 값이 클 수록, prediction interval(예측 구간)의 크기가 더욱 급격하게 늘어난다.
• d=0에서, 장기 예측 표준 편차는 과거 데이터의 표준 편차와 가까워지고, 모든 예측 구간이 같아진다.
  • 예시
    • c=0, d=0이면, 장기 예측값이 0에 가까워질 것입니다.
    • c=0, d=1이면, 장기 예측값이 0이 아닌 상수에 가까워질 것입니다.
    • c=0, d=2이면, 장기 예측값이 직선 형태로 나타나게 될 것입니다.
    • c≠0, d=0이면, 장기 예측값이 데이터의 평균에 가까워질 것입니다.
    • c≠0, d=1이면, 장기 예측값이 직선 형태로 나타나게 될 것입니다.
    • c≠0, d=2이면, 장기 예측값이 2차 곡선 추세로 나타나게 될 것입니다.
• Figure 8.8을 다시 보면, c≠0, d=0이므로
  예측 구간은 마지막 몇 개의 예측 수평선에 대한 경우와 거의 같고,
  점 예측값은 데이터의 평균과 같다.
  
• $p$ 값은 데이터에 주기가 존재할 때 중요하다.
  • 주기적인 데이터에서 예측값을 얻기 위해 $p \ge 2$라는 조건이 추가된다.
  • 예시
    • AR(2) 모델은 $ϕ^2_1+4ϕ_2<0$ 일 때, 주기적이다.
    • 이 때, 주기는 평균 기간과 같다.
      $cycle = \frac{2\pi}{\arccos(-ϕ_1(1-ϕ_2)/(4ϕ_2))}$

8.5.3 ACF와 PACF 그래프

: 적절한 $p, q$ 선정

• 보통 time plot만 보고 $p, q$를 선정할 수 없고, ACF, PCAF 그래프를 이용해야 한다.

• ARIMA(p,d,0)이거나 ARIMA(0,d,q) 일 때,
  즉, AR이나 MA의 차수 중 하나가 0일 때, 나머지 차수를 결정한다면, 이 때 ACF와 PACF가 유용하다.

• ACF 그래프

  • 서로 다른 $k$값에 대해, $y_t$와 $y_{t-k}$의 관계를 측정하는 자기상관값 그래프

• y_t와 y_t-1의 상관관계가 있고, y_t-1와 y_t-2의 상관관계가 있으니, y_t와 y_t-2도 상관관계를 가질 수 있음 → 문제가 발생할 수 있다.

  • partial autocorrelations(부분 자기상관값)을 통해 해결한다.

• partial autocorrelations

  • 시차($1, 2, 3, ..., k-1$)의 효과를 제거한 뒤, $y_t$와 $y_{t-k}$간의 관계를 측정한다.
  • 첫 번째 partial autocorrelation은 그대로
  • 각 partial autocorrelation은 autoregressive model의 마지막 계수처럼 측정할 수 있다.
    • $k$번째 partial autocorrelation 계수 $α_k$는 AR(k) 모델에서 계수 $ϕ_k$ 측정값과 같다.

• 차분을 구한 데이터의 ACF와 PACF 그래프의 패턴에 따라 AR 혹은 MA의 차수가 0인지 추측할 수 있다.

  • ARIMA(p,d,0) : MA의 차수가 0
    • ACF가 지수적으로 감소하거나 sin 함수 모양인 경우
    • PACF 그래프에서 시차 p에 뾰족한 막대가 존재하지만, 그 이후에 없을 때
  • ARIMA(0,d,q) : AR의 차수가 0
    • PACF가 지수적으로 감소하거나 sin 함수 모양인 경우
    • ACF 그래프에서 시차 q에 뾰족한 막대가 존재하지만, 그 이후에 없을 때

• 예시

  • 아래 Figure 8.9와 8.10은 미국 소비 데이터의 ACF와 PACF 그래프이다.
    
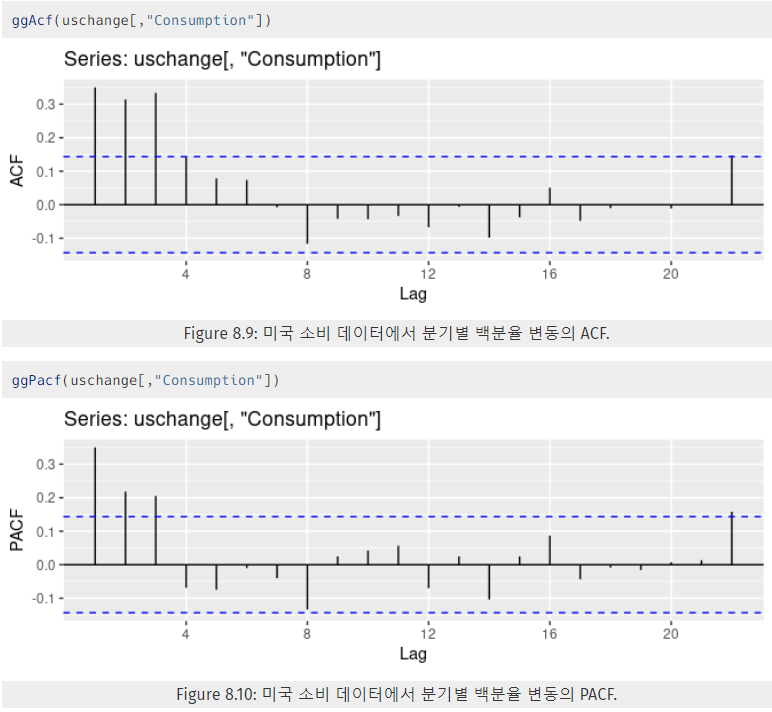
  • ACF는 시차 4까지 유의미한 뾰족 막대가 있고, 이전에 3개의 유의미한 뾰족 막대가 존재한다. 그 이후에는 없다.
  • PACF는 시차 3까지 유의미한 뾰족 막대가 있고, 그 이후에는 없다.
  • 시차 22는 뒤처짐으로 인해 한 번 정도 경계를 벗어나는 것은 무시할 수 있다.
  • PACF에서 첫 3의 뾰족한 막대가 감소하는 경향이 있다.
  • 이를 통해 ARIMA(3,0,0)이 적절할 수 있다 생각한다.

  ㄟ(▔,▔)ㄏ
  오히려 AR의 차수가 0이지 않을까?
  Figure 8.9는 MA의 차수가 0일 때의 패턴과 
  AR의 차수가 0일 때의 패턴이 모두 나타난다고 생각한다.

8.6 추정과 차수 선택

8.6.1 최대 가능도 추정

• 매개변수 $c, ϕ_1,…,ϕ_p, θ_1,…,θ_q$ 를 추정하는 방법
• R에서 ARIMA 모델을 계산할 때, 최대 가능도 추정(maxium likelihood estimation)을 사용한다.
• 예측값이 관찰한 데이터와 같아질 확률이 가장 높은 매개변수 값을 찾는다.
• 실제로 R은 데이터의 log likelihood 값을 산출하고, 이를 최대화 하는 매개변수 값을 찾는다.
  • log likelihood : 추정한 모델에서 나온 관측값의 확률 log

8.6.2 정보 기준

• 차분 차수($d$)를 고를 때는 도움이 되지 않고,
  $p$와 $q$값을 고를 때만 도움이 된다.
  • 차분을 통해 likelihood(가능도)를 산출하기 때문에 서로 다른 차수로 차분을 구한 모델의 AIC 값을 비교할 수 없기 때문이다.
• 이전에 회귀에서 예측변수 x를 고를 때 유용했던 AIC (Akaike 정보 기준)을 ARIMA의 차수 결정 시에도 사용한다.
• 아카이케의 정보 기준(AIC: Akaike’s information Criterion)
  $AIC=−2log(L)+2(p+q+k+1)$
  • $L$ : 데이터 가능도
    • c≠0 이면 k=1 이고, c=0 이면 k=0이다.
  • 괄호 안의 마지막 항이 모델의 매개변수 개수이다.
    ($σ^2$과 잔차의 분산도 포함한다.)
• 수정된 아카이케 정보 기준 (AICc)
  $AICc = AIC + \frac{2(p+q+k+1)(p+q+k+2)}{T-p-q-k-2}$
• 베이지안 정보 기준
  $BIC = AIC + [log(T)-2](p+q+k+1)$
• 위와 같은 정보 기준(AIC, AICc, BIC)이 최소화 된 것이 좋은 모델이다.

8.7 R에서 ARIMA 모델링

생략 (해당 교재 내용 link)

8.8 예측하기

8.8.1 점 예측값

• 점 예측값을 구하는 방법 3단계
  1. $y_t$를 좌변으로, 나머지를 모두 우변으로 오도록 ARIMA 식을 전개한다.
  2. t를 T+h로 변환한다. (T는 현재 시점)
  3. 우변에서 미래 관측값을 예측값으로 바꾸고,
     미래 오차값을 0으로 바꾸고,
     과거 오차값을 해당 잔차로 바꾼다.
  4. $h=1$로 시작하여 모든 예측값을 계산할 때까지
     $h=2, 3, ...$로 1~3단계를 반복한다.

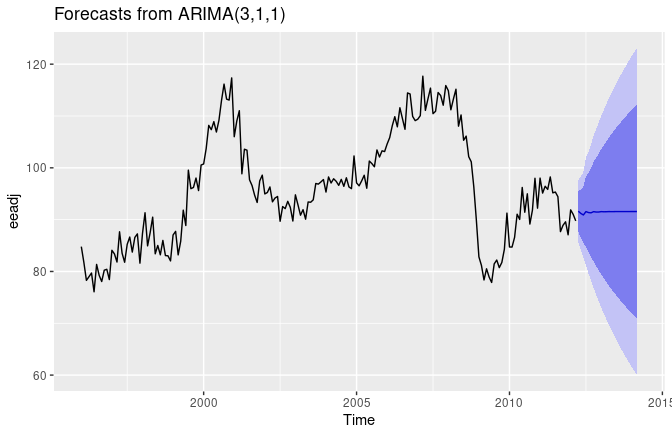
예시 : ARIMA(3,1,1)

• ARIMA 식
  $(1−\hatϕ_1B−\hatϕ_2B^2−\hatϕ_3B^3)(1−B)y_t=(1+\hatθ_1B)ε_t$
  • 좌변 전개
    $[1−(1+\hatϕ_1)B+(\hatϕ_1-\hatϕ_2)B^2+(\hatϕ_2-\hatϕ_3)B^3+\hatϕ_3B^4]y_t=(1+\hatθ_1B)ε_t$
  • 후방이동 연산자 적용
    $y_t−(1+\hatϕ_1)y_{t-1}+(\hatϕ_1-\hatϕ_2)y_{t-2}+(\hatϕ_2-\hatϕ_3)y_{t-3}+\hatϕ_3y_{t-4}=ε_t+\hatθ_1ε_{t-1}$

1. $y_t$를 좌변으로, 나머지를 모두 우변으로 오도록 ARIMA 식을 전개한다.

   $y_t=(1+\hatϕ_1)y_{t-1}-(\hatϕ_1-\hatϕ_2)y_{t-2}-(\hatϕ_2-\hatϕ_3)y_{t-3}-\hatϕ_3y_{t-4}+ε_t+\hatθ_1ε_{t-1}$

2. t를 T+1로 변환한다. (h=1)

   $y_{T+1}=(1+\hatϕ_1)y_{T}-(\hatϕ_1-\hatϕ_2)y_{T-1}-(\hatϕ_2-\hatϕ_3)y_{T-2}-\hatϕ_3y_{T-3}+ε_{T+1}+\hatθ_1ε_{T}$

3. 우변에서 미래 관측값을 예측값으로 바꾸고,
   미래 오차값을 0으로 바꾸고,
   과거 오차값을 해당 잔차로 바꾼다.

   • 시간 T까지의 관측값을 가지고 있을 때, 우변의 $ε_{T+1}$를 제외하고 모두 알고 있다.
   • 이 때, 이 값을 0으로 두고, $ε_{T}$를 관측 잔차 $e_T$로 둔다.
   $\hat y_{T+1|T}=(1+\hatϕ_1)y_{T}-(\hatϕ_1-\hatϕ_2)y_{T-1}-(\hatϕ_2-\hatϕ_3)y_{T-2}-\hatϕ_3y_{T-3}+\hatθ_1e_{T}$

4. t를 T+2로 변환한다. (h=2)

   $\hat y_{T+2|T}=(1+\hatϕ_1)\hat y_{T+1|T}-(\hatϕ_1-\hatϕ_2)y_{T}-(\hatϕ_2-\hatϕ_3)y_{T-1}-\hatϕ_3y_{T-2}$

• 이러한 과정을 반복하며 모든 미래 시점에 대한 점 예측값을 산출한다.

8.8.2 예측 구간

• ARIMA의 예측 구간은 잔차와 관련이 없고, 잔차는 정규분포를 따른다는 가정에 기초한다.
  • 예측구간을 내기 전, 항상 ACF 그래프와
    잔차 히스토그램을 통해 가정 성립 여부를 파악한다.
• 일반적으로 예측 수평선이 증가할수록,
  ARIMA 모델로 얻은 예측구간은 증가한다.
• 정상성을 나타내는 모델(즉 $d=0$)인 경우,
  긴 수평선에 대해 예측구간이 모두 같도록 수렴한다.
• $d \ge 1$인 경우, 시간이 지날수록 예측구간은 계속 증가한다.

예시 1. $\hatσ$ = 잔차의 표준편차

• 95% 예측 구간은 $\hat y_{T+1|T} \plusmn 1.96\hatσ_h$로 주어진다.
• 모든 ARIMA 모델에서 적용된다.

예시 2. ARIMA(0,0,q)

• ARIMA(0,0,q) 모델
  $y_t = ε_t + \sum^q_{i=1}θ_iε_{t−i}$
• 추정한 예측 분산
  
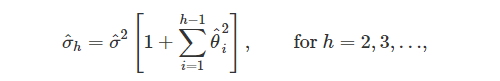
• 95% 예측 구간은 $\hat y_{T+1|T} \plusmn 1.96\sqrt{\hatσ_h}$로 주어진다.

8.9 계절성 ARIMA 모델들

• 지금까지 살펴본 비계절성 ARIMA 모델에 계절성 항을 포함하여 구성한다.
  • 비계절성 부분 : $(p,d,q)$
  • 계절성 부분 : $(P,D,Q)_m$
• m : 매년 관측값의 개수
• 계절성 부분도 비계절성 부분과 비슷하게 구성되지만, 계절성 주기의 후방이동을 포함한다.
• 예시 : 상수가 없는 $ARIMA (1,1,1)(1,1,1)_4$
  • m=4 이므로 계절성을 지닌 분기별 데이터임을 알 수 있다.
  • 단순하게 비계절성 항에 계절성 항을 곱해준다.
    $(1−ϕ_1B) (1−Φ_1B^4)(1−B)(1−B^4)y_t=(1+θ_1B) (1+Θ_1B^4)ε_t$

8.9.1 ACF/PACF

• 모델의 계쩔성을 파악하는 방법
• AR이나 MA 모델의 계절성 부분은 PACF와 ACF의 계절성 시차에서 확인할 수 있다.
• 예시 : $ARIMA(0,0,0)(0,0,1)_{12}$
  • ACF에 시차 12에서 나타나는 뾰족한 막대가 존재한다.
  • PCAF의 계절성 시차가 지수적으로 감소한다.(시차 12, 24, 36, ...)
• 계절성 ARIMA 모델의 적절한 계절성 차수 $(P,D,Q)_m$를 선정할 때, 계절성 시차를 고려해야한다.

예제 : 유럽 분기별 소매 거래

1. time plot을 보고, 정상성, 계절성 여부 파악
   

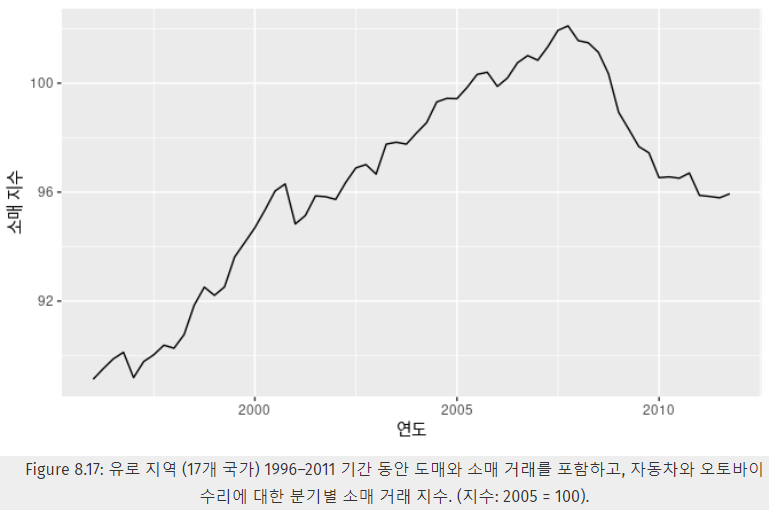
• 정상성 X, 계절성 O
• 계절성 차분을 먼저 구하여 정상성 O를 만든다.
  • 1차 차분으로 정상성 X 라면, 한 번 더 차분을 진행한다.

2. ACF, PACF에 기초하여 적절한 ARIMA 모델을 찾는다.
   

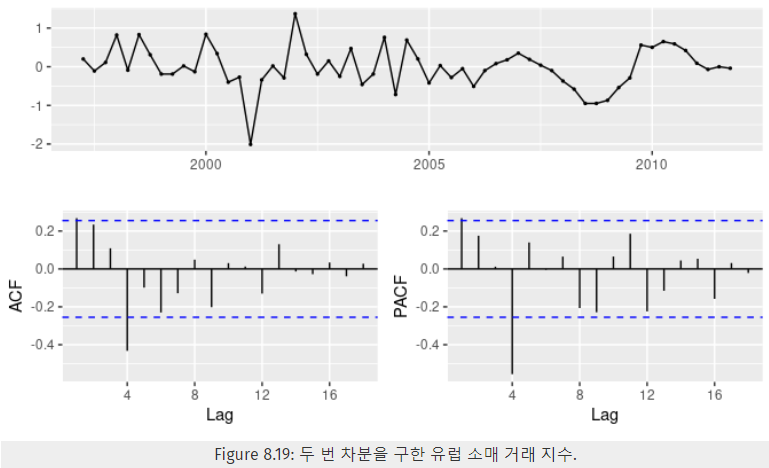
• ACF에서 시차 1의 유의미한 뾰족 막대 → 비계절성 MA(1)
• ACF에서 시차 4의 유의미한 뾰족 막대 → 계절성 MA(1), 관측값 개수 m=4
  => 1차 차분과 계절성 차수을 나타내는 $ARIMA(0,1,1)(0,1,1)_4$

  ㄟ(▔,▔)ㄏ
  위에서 정상성 확보를 위해 2차 차분까지 했다고 설명되어있는데 
  왜 여기서는 1차 차분인건지?

3. ARIMA 모델의 잔차를 확인한다.
   

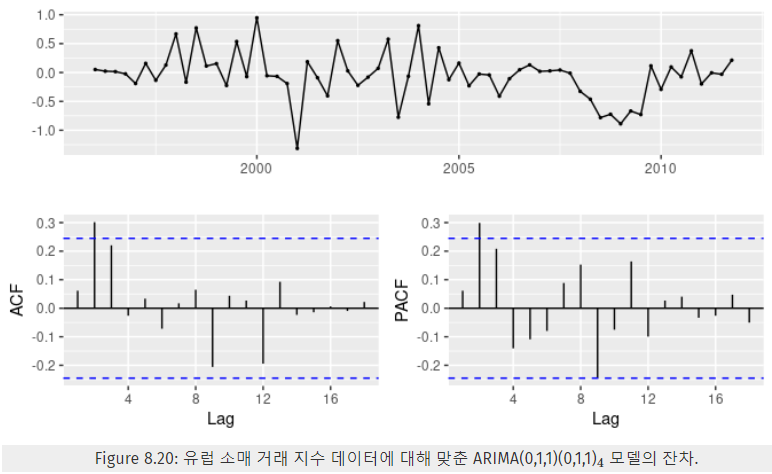
• ACF와 PACF 둘 다 시차 2에서의 유의미한 뾰족 막대
• 시차 3에서 덜 유의미하지만 뾰족한 막대
  => 이렇게 유의미한 뾰족 막대가 등장한다면,
  추가적인 비계절성 항을 추가할 것을 고려해야 한다.

4. 비계절성 항을 조절하며 정보 기준 산출 → 최소값

• 정보 기준을 비교하는 것은 같은 차수로 차분을 구한 ARIMA 모델에 대해서만 의미가 있다.
• $ARIMA(0,1,3)(0,1,1)_4$의 AICc : 68.53
• $ARIMA(0,1,2)(0,1,1)_4$의 AICc : 74.36
• ...
• AICc가 가장 작은 $ARIMA(0,1,3)(0,1,1)_4$ 선택

5. 다시 선택한 ARIMA 모델로 잔차를 확인한다.
   

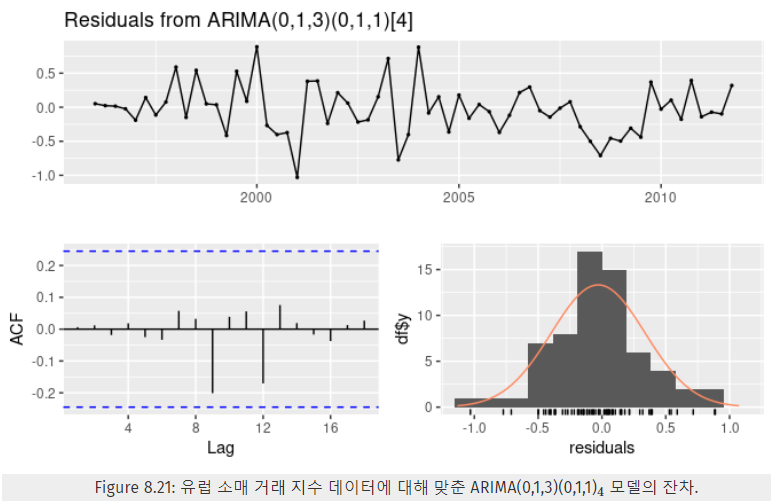
• ACF 그래프를 보면 모든 잔차가 유의미한 범위 안에 들어오고, 뾰족한 막대가 없다. → 백색잡음
  • 추가로 융-박스 검정을 통해 잔차에 자기상관관계가 없음을 확인할 수 있다.
• 예측을 진행할 계절성 ARIMA 모델 선택을 완료한 것이다.

6. 확인 절차를 거친 ARIMA 모델을 통해 예측을 진행한다.
   

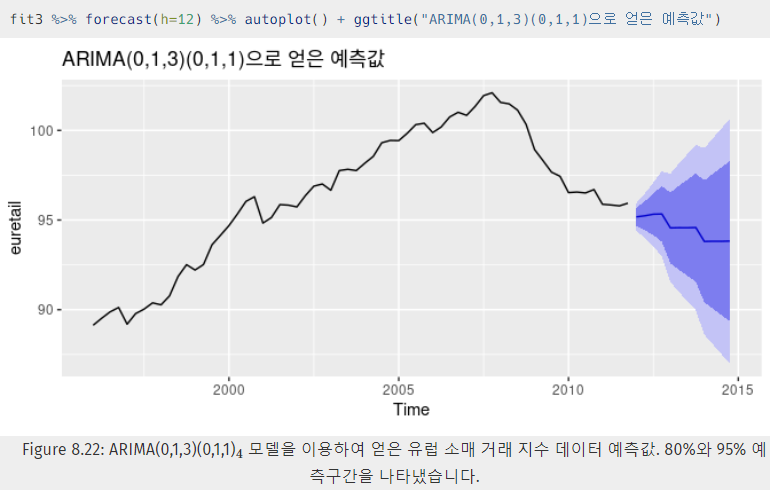
• 2차 차분을 통해 구했기 때문에 예측값이 데이터의 최근 추세를 따라간다.

  ㄟ(▔,▔)ㄏ
  왜 2차 차분 때문에 최근 추세를 따라가나?
  
  c=0, d=2이면, 장기 예측값이 직선 형태로 나타나게 될 것입니다.
  c≠0, d=2이면, 장기 예측값이 2차 곡선 추세로 나타나게 될 것입니다.
  
  위 내용이 최근 추세를 따라간다는 것에 대한 반증이 되는지 궁금하다.

예제 : 호주 코르티코 스테로이드 약물 판매량

• 생략(해당 교재 내용 link)

8.10 ARIMA vs ETS

• 비교 예제에 대한 설명 (해당 교재 내용 link)
• 모든 ETS 모델은 정상성 X의 경우,
  ARIMA 모델은 정상성 O의 경우에 맞는다? 성능이 좋다?

8.10.1 비계절성 데이터에서 ARIMA와 ETS 비교

• 비교를 위해 시계열 교차검증을 사용한다.
  • 시계열 데이터가 아주 긴 경우에는 시계열 교차 검증보다 데이터를 학습 데이터와 테스트 데이터로 나누어 사용한다.
• 비교 결과
  • MSE 값에 기초해서 보면 ETS 모델이 더 낮은 tsCV 통계량을 갖는다. (낮을수록 좋은 모델이다.)

8.10.2 계절성 데이터에서 ARIMA와 ETS 비교

• 학습 데이터와 테스트 데이터로 나누어 사용한다.
• ARIMA와 ETS 두 모델 모두 잔차가 백색잡음인 것 같은 결과를 보인다.
• 비교 결과
  • 학습 데이터 예측에서는 ARIMA가 살짝 우세했지만, 테스트 데이터 예측에서는 ETS가 살짝 우세하였다.
• 결론적으로 어떤 유형의 데이터이던 간에 절대적으로 ARIMA가 더 좋다고 할 수 없다.