[Time Series] 비선형 회귀 모델

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 5장 8절을 참고하여 작성하였습니다.

5.8 비선형 회귀

• 선형 관계로 가정할 수 없는 복잡한 경우에 사용한다.
• 회귀 모델을 추정하기 전, 목표 예상변수 y와 예측변수 x를 변환시킨다. (주로 log 변환을 사용한다.)
• x에 log가 붙으면 선형-로그 형태
• y에 log가 붙으면 로그-선형 형태
• x, y에 둘 다 log가 붙으면 로그-로그 형태이다.
• 이 때, 모델의 매개변수는 여전히 선형적이다.
  $log y = β_0 +β_1log x + ε$
• log x 앞에 붙은 기울기 β_1은 탄력성이라고 하며, x가 1% 증가할 때, y의 평균 백분율 변화율이다.
• 변수를 log 변환하기 위해서는 모든 관측값이 0보다 커야한다. 아래와 같이 오차값을 활용해 0이 아닌 값이 되도록 한다.
  $y=f(x)+ε$
  • 여기서 f(x)는 비선형 함수이다.
    선형회귀에서는 f(x) = β_0 + β_1x이지만,
    비선형회귀에서는 log 변환과 같은 x에 대한 변환이 포함된 함수이다.
• 조각별 선형(piecewise linear)
  • f(x)의 기울기가 변할 수 있는 점(매듭)을 반영하여 표현하는 방법
  • x_1, t = x로 두고, 변수 x_2, t를 활용한다.
    
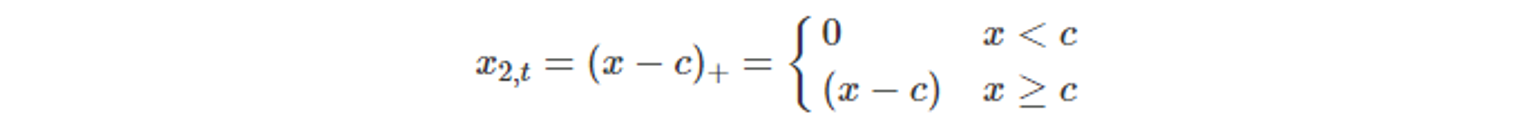
  • (x-c)_+ 는 양수일 때 (x-c), 음수일 때 0을 나타낸다.
    ⇒ c 점에서 기울기가 구부러진다.
  • 이러한 조각별 선형은 회귀 스플라인의 한 형태이다.
• 회귀 스플라인(regression splines)
  • 비선형 회귀를 표현하는 방법
    
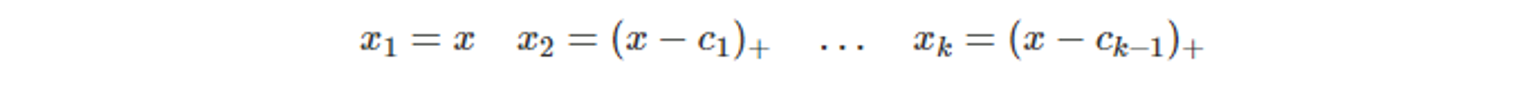
    • 매듭(기울기가 변하는 점) : c_1, … , c_k-1 (k-1개) 를 가지는 조각별 선형 형태이다.
      
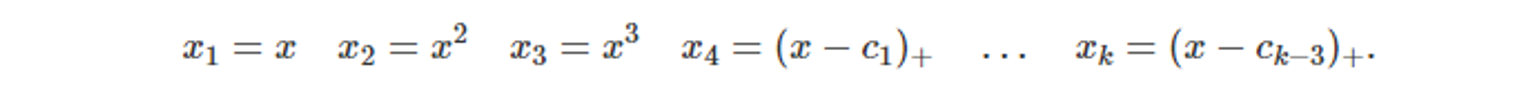
    • 각 x_k (k=1, 2, …)에 2차원 3차원 식을 대입함으로서 3차 회귀 스플라인을 작성한다.
    • 3차 회귀 스플라인이 데이터에 더 적합한 모습을 보인다. 하지만, x가 과거 데이터가 아닐 때, 예측값 y를 신뢰할 수 없다.
      

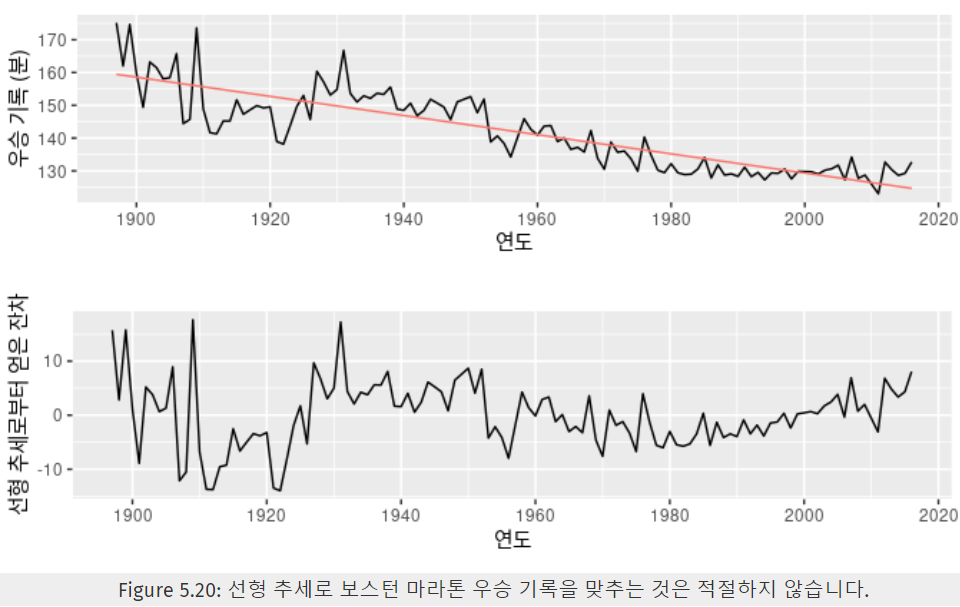
5.8.1 비선형 추세로 예측하기

• 선형 추세로 예측 방법 : x=t로 두고 시계열에 맞추기
• 가장 간단한 비선형 추세로 예측 방법 : 2차 이상의 추세를 시계열에 맞추기
  ⇒ 권장 X
  ㄴ Why? 알려진 데이터의 추세에서 알려지지 않은 값을 추론할 경우 예측값이 부정확해서
  
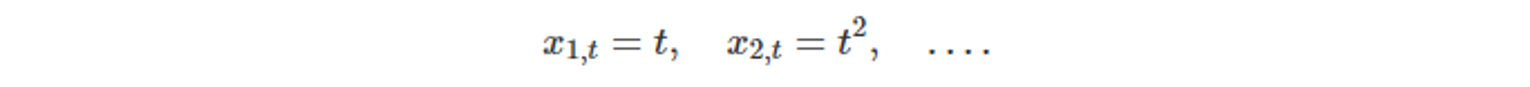
• 더 나은 방식
  • 선형조각으로 구성된 비선형 추세
    : 조각별 선형 방식에서 시간에 따라 매듭을 맞추는 것
    
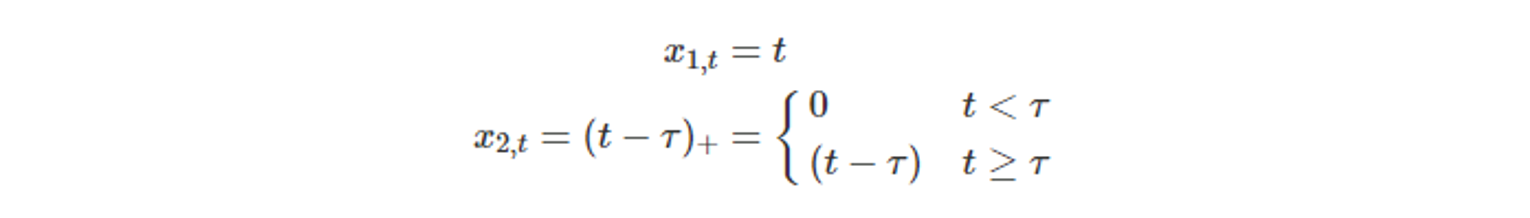
    • 시간 τ 에서 추세가 휘는 것을
      시점 t일 때, τ를 매듭으로 생각하면 위와 같이 표현할 수 있다.
    • x_1,t와 x_2,t의 관련 계수가 β_1와 β_2 일 때,
      β_1는 τ 시점 전의 추세 기울기, β_1 + β_2 는 τ 시점 후의 추세 기울기
    • (t-τ)_+ 에 변수를 추가한다면 매듭을 추가하여 더 구부러지게 할 수 있다.