[Time Series] 회귀 모델 행렬 정식화

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 5장 7절을 참고하여 작성하였습니다.

5.7 행렬 정식화

인라인 수식: $f(x) = \sqrt{1+x}, \quad x \ge -1$

• 다중 회귀 모델
  $y_t = β_0 + β_1x_{1,t} + β_2x_{2,t} + ... + β_kx_{k,t} + ε_t$
  • 오차 ε_t의 평균은 0이고, 분산은 σ^2이다.
• 행렬 형태
  $\bold y=(y_1, ... , y_T)', \bold ε=(ε_1, ... , ε_T)', \bold β=(β_0, ... , β_k)'$
  
  • 이러한 행렬들을 통해 다중 회귀 모델 식을 작성하면,
    $\bold y= \bold X \bold β + \bold ε$
    • 오차의 집합 ε의 평균은 0이고, 분산은 σ^2 * I 이다.
    • 행렬 X 의 행은 T개이며, 관측값 수를 나타낸다.
    • 행렬 X 의 열은 k+1개이며, 첫 번째 열이 1로 이루어져 있어 절편을 나타낸다.

5.7.1 최소 제곱 추정

• 아래와 같이 오차의 내적 값을 표현하는 식을 최소화 하여 “최소 제곱 추정”을 진행한다.
  
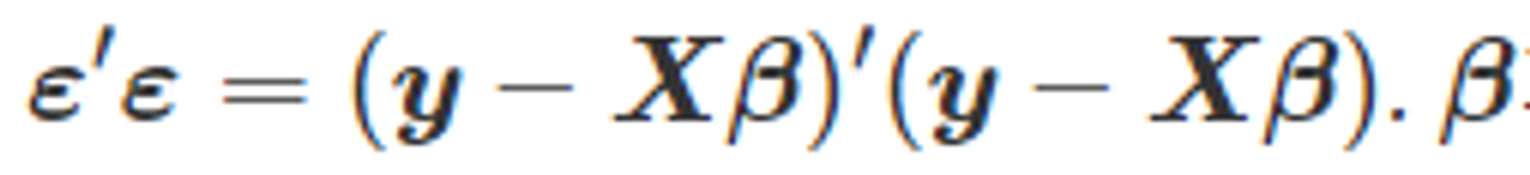
• 이 값을 최소화 하기 위해 β는 아래와 같은 값이 되어야 한다. (”정규식” 이라고도 한다.)
  
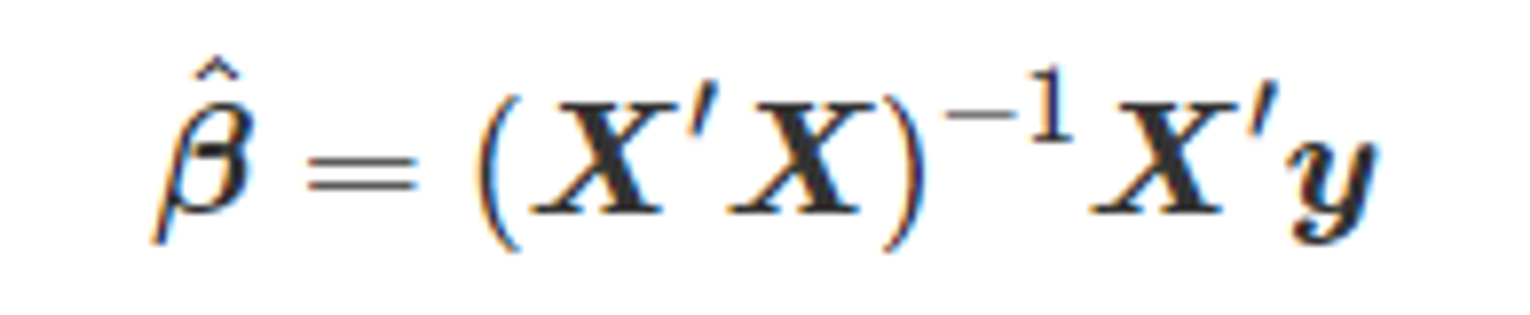
• 위 식에는 역행렬 X’X 가 필요한데, 만약 X 전체가 column rank가 아니라면, X’X는 singular 하여 추정할 수 없게 된다.
• 잔차 분산
  

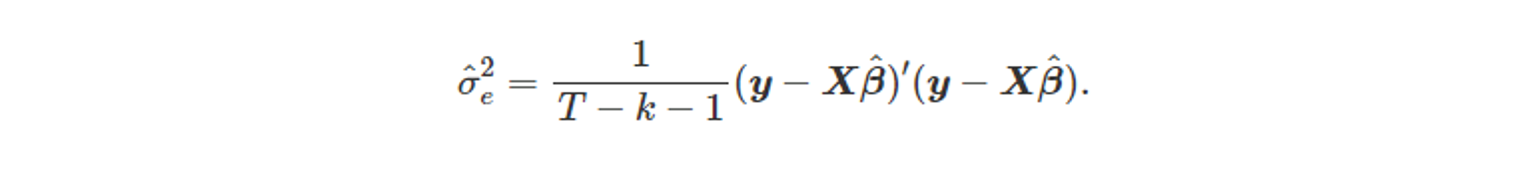
5.7.2 적합값과 교차검증

• [5.7.1 최소 제곱 추정]의 수식을 기반으로 산출한 정규식은 아래와 같다.
  
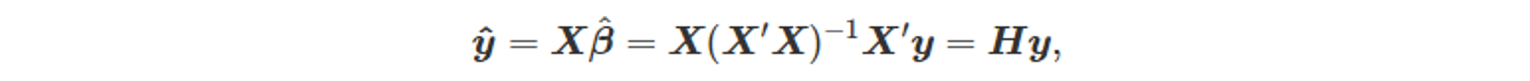
  • 여기서 H = X(X’X)^-1X’ 이고, H는 y_hat을 계산할 때 y에 곱해지는 계수 형태이므로, “hat-matrix”라고도 한다.
• H의 대각 성분 값을 h1, … , h_T로 쓰면, 아래 식을 통해 교차검증이 가능하다.
  
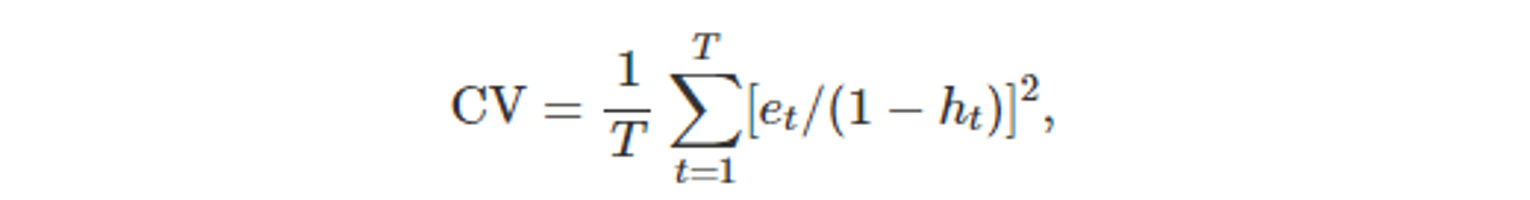
  • 여기서 e_t 는 모델의 예측값에 관측값을 맞추기 위한 잔차이다.
  • 따라서, CV 통계를 계산할 때 T개의 나뉜 모델을 실제로 맞출 필요가 없습니다.

5.7.3 예측값과 예측구간

• 예측값 y_hat을 산출하기 위해 필요한 X의 특정 행 벡터를 x^*라 할 때, 아래와 같은 수식을 구할 수 있다.
  
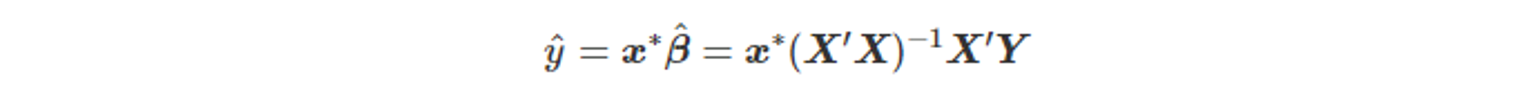
  • 이 때의 분산은 아래와 같다.
    
  • 이 때의 95% 예측구간은 아래와 같다.
    
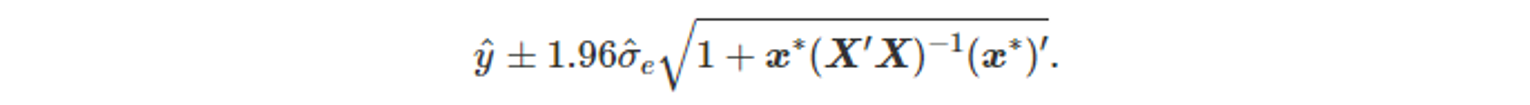
  • 이 식은 오차항 ε 때문에 생기는 불확실성과
    계수의 값을 추정함으로써 발생하는 불확실성을 고려한다.
    하지만 x^*에 있는 모든 오차를 무시하기 때문에 예측변수의 미래값이 확실하지 않다면, 예측구간이 매우 좁게 계산된다.