[Time Series] 시계열 분해 방법

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 6장 1절을 참고하여 작성하였습니다.

6.1 시계열 성분

6.1.1 덧셈 분해(additive decomposition)

• 시계열 수준에 따라 계절성이나 추세-주기(trend-cycle)가 변하지 않을 때, 덧셈 분해가 적절하다.
  $y_t=S_t+T_t+R_t$
  • y_t : 데이터
  • S_t : 계절성 (Seasonal)
  • T_t : 추세-주기 성분(Trend)
  • R_t : 나머지 성분(Reminder)

6.1.2 곱셈 분해(multiplicative decomposition)

• 시계열 수준에 따라 계절성이나 추세-주기(trend-cycle)가 변할 때, 덧셈 분해가 적절하다. (주로 경제분야)
  $y_t=S_t*T_t*R_t$
• log 변환을 통해 시간에 따라 값이 안정적이게 만들고, 덧셈 분해를 사용할 수 있다.
  $logy_t=logS_t+logT_t+logR_t$

6.1.3 예제 : 전자 장비에 대한 신규 주문 지수 데이터

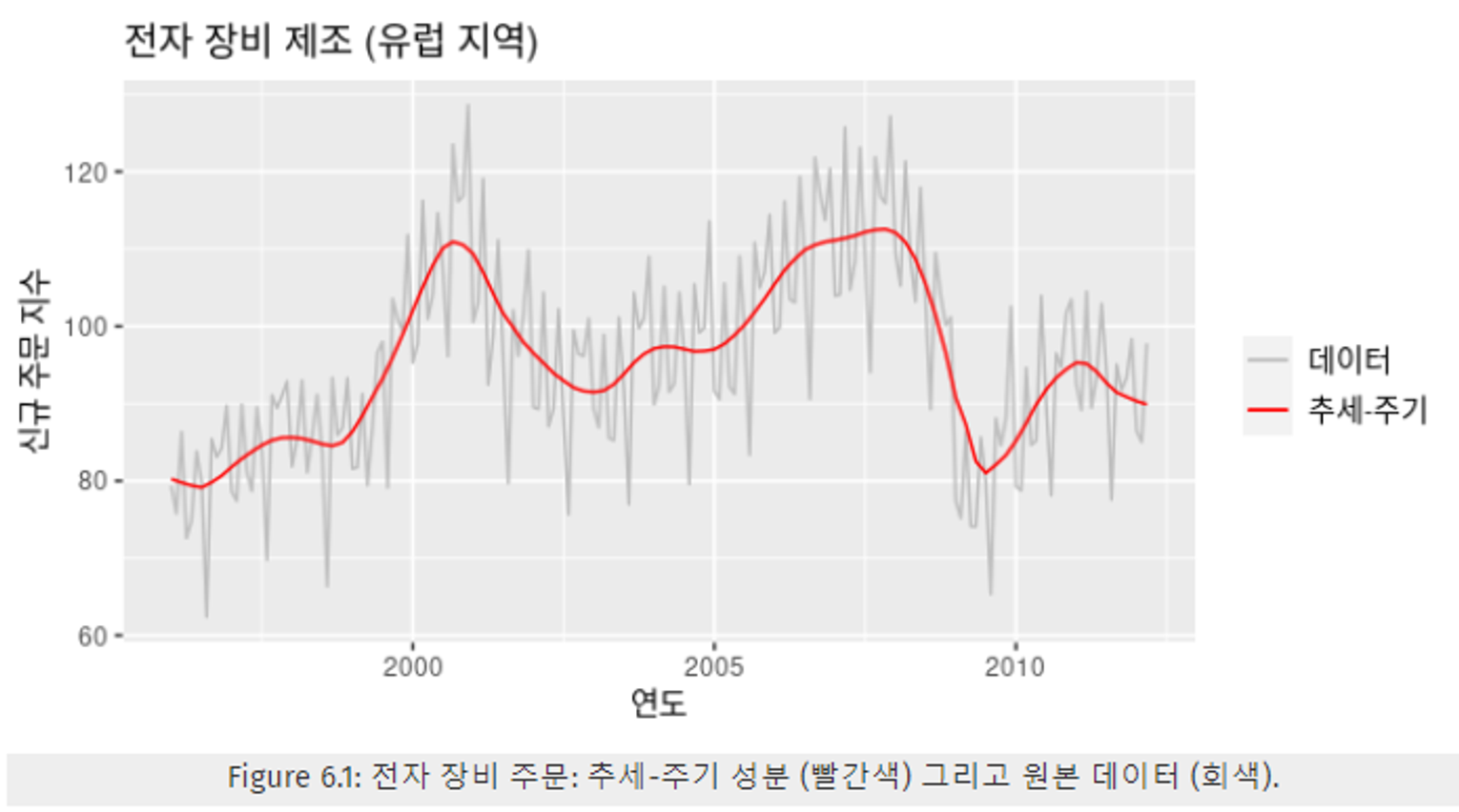
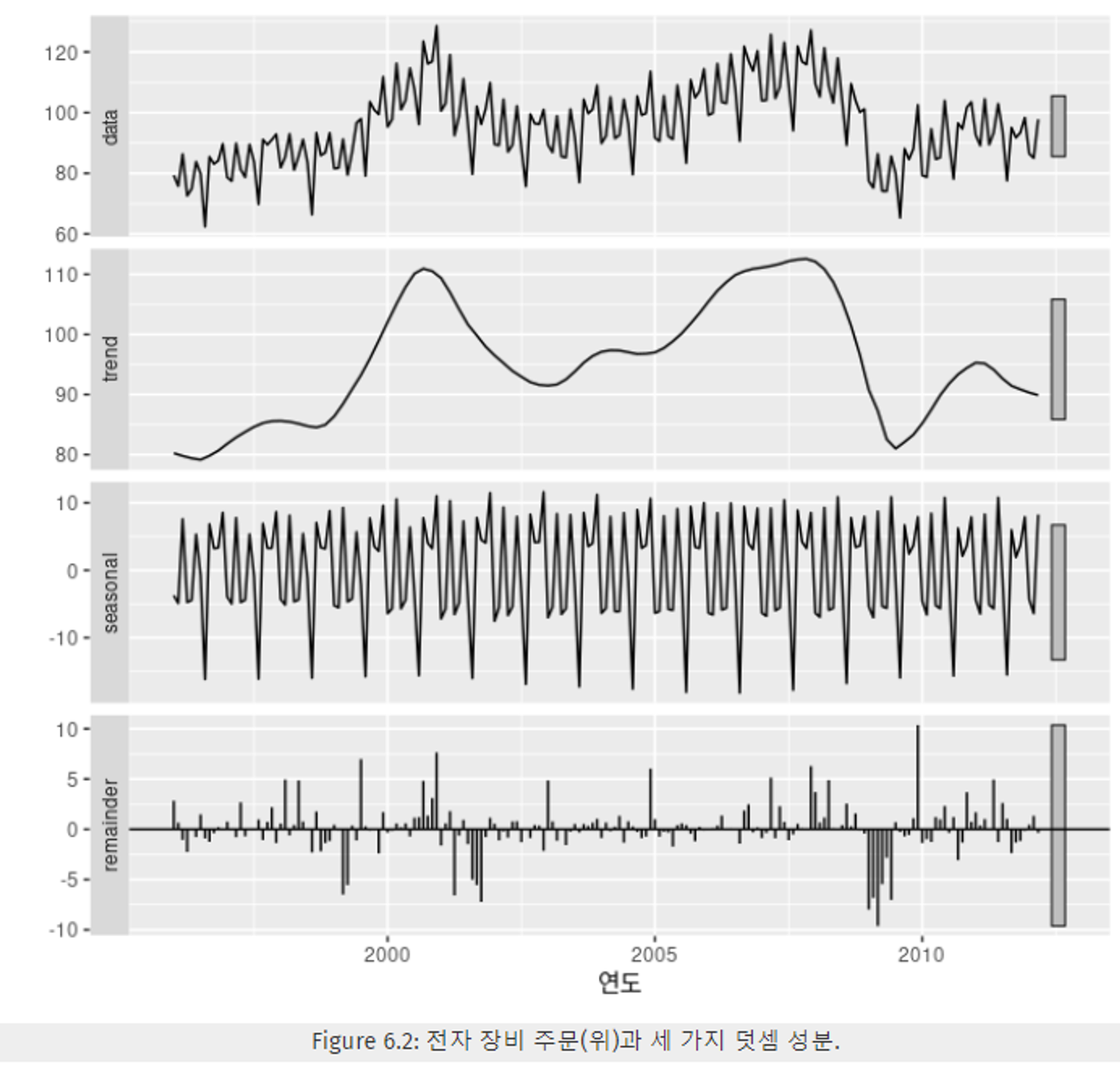
• Figure 6.2의 trend, seasonal, remainder을 더하면, data가 나온다.
• seasonal은 시간에 따라 느리게 변한다.
• 두 개 연도 마다 비슷한 trend를 가진다.
• 서로 멀리 떨어진 연도는 다른 seasonal 패턴을 가진다.
• 그래프 오른쪽의 회색 막대 : 성분의 상대적인 눈금

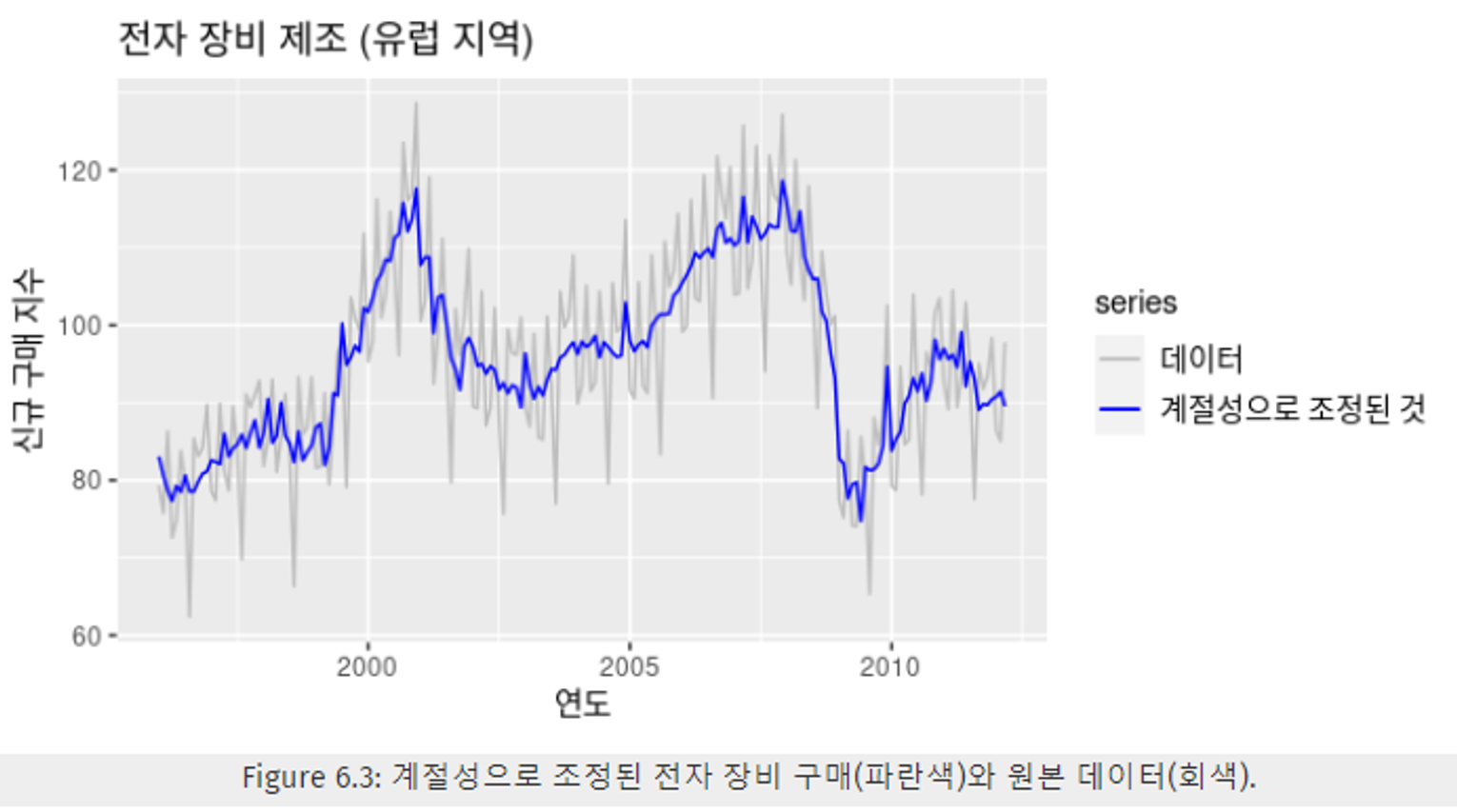
• 계절성을 고려하고 싶지 않을 때, 계절성을 제거하여 데이터를 확인한다.
  • 예 : 월별 실업률 데이터를 다룰 때, 계절성 보단 중요한 경제 상황에 따른 변동을 보고 싶으므로 데이터를 계절성으로 조정한다.
• 이러한 시계열 데이터는 “매끄럽지 않고” “상승세 or 하락세”로 표현될 수 있다.
• 시계열 데이터에서 전환점을 살펴보기 위함, 어떤 방향으로의 변화를 해석하기 위함이라면,
  계절성으로 조정 X (나머지까지 포함됨) → 추세-주기(trend-cycle) 성분을 사용한다.