온라인 Forecasting 교재 [Forecasting : Principles and Practice] 6장 2절을 참고하여 작성하였습니다.
6.2 이동평균(MA : Moving Average)
- 1920~1950년 까지 주로 사용된 고전적인 시계열 분해 방법
- 그 첫 번째 단계는 추세-주기(trend-cycle)를 측정하기 위한 이동평균 방법을 사용한다.
6.2.1 이동 평균 평활
- 차수 m의 이동 평균을 아래와 같이 표현할 수 있다.
(차수가 3인 경우 현재 시점부터 과거 3개 이전의 시점까지의 데이터 영향도를 보겠다는 뜻)
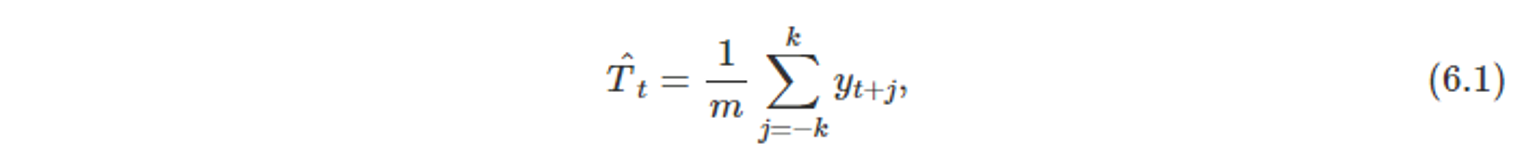
- m = 2k + 1
- 식을 보면 t 시점으로부터 [-k, +k] 기간의 관측값에 대한 평균을 나타낸다.
- k 기간 안의 시계열 값을 평균으로 산출함으로써 시간 t의 추세-주기(trend-cycle)를 측정한다.
- 평균을 산출함으로써 무작위성을 줄이고, 매끄러운 추세-주기(trend-cycle) 성분만 남긴다.
- 차수 m의 이동 평균 이라는 의미에서 m-MA 라고 부른다.
예시 : 호주 남부의 매년 주거용 전기 판매량
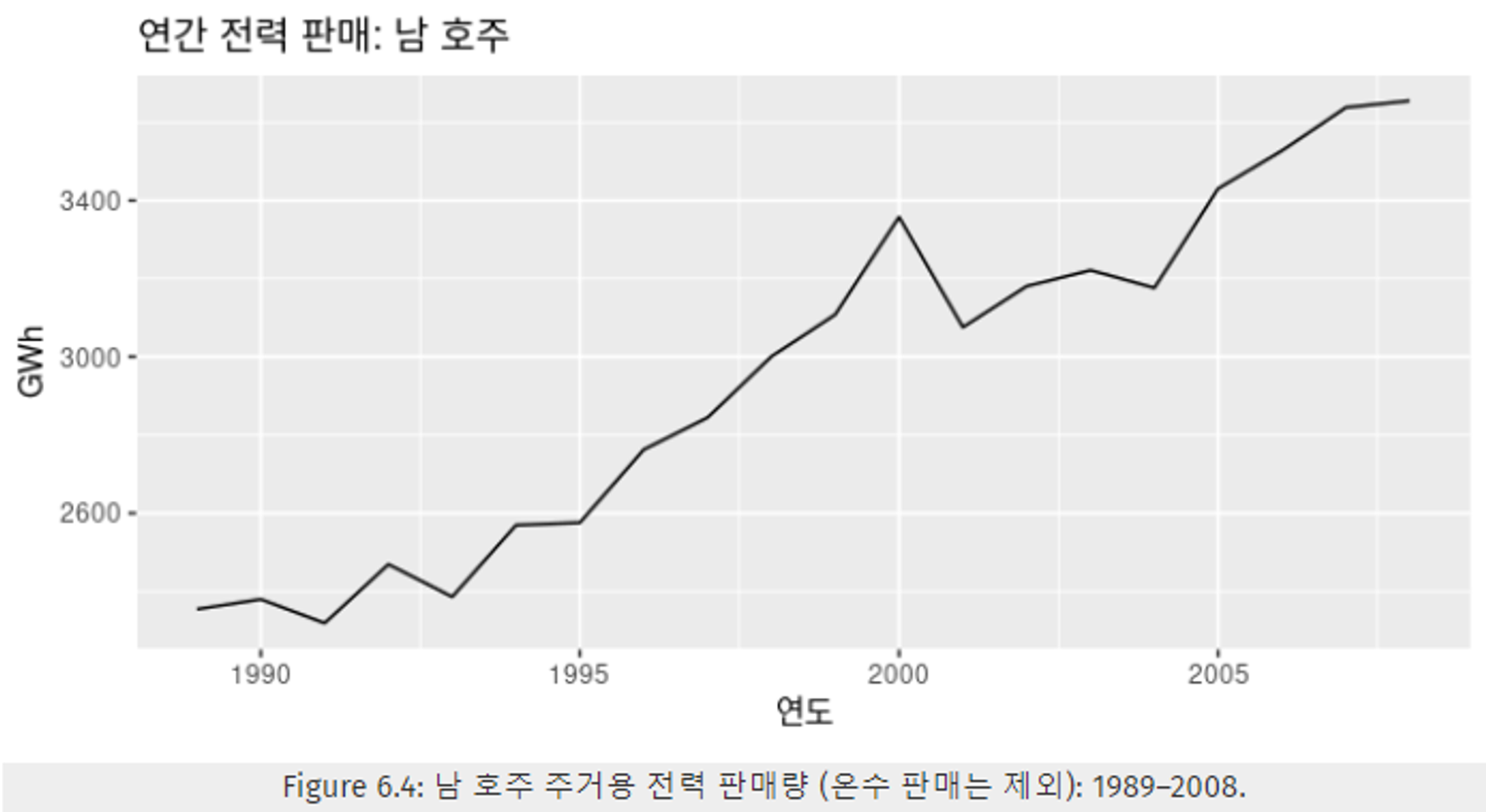
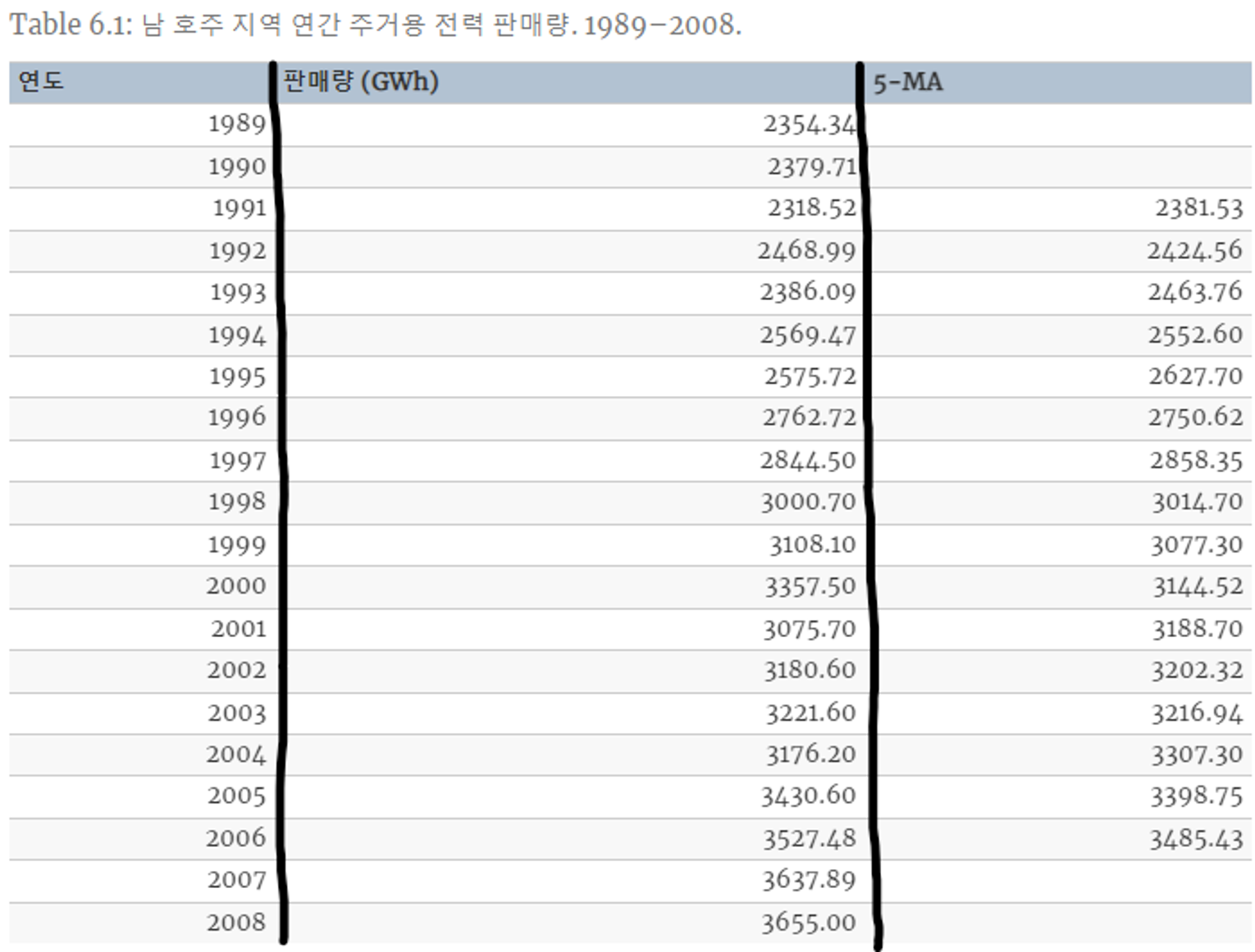
- Table 6.1의 판매량(GWh)는 5년 간의 관측값의 평균이다. → 차수가 5이기 때문에
- 판매량(GWh) : 기준 년도 + “향후 4년”
- Table 6.1의 “5-MA” 는 추세-주기(trend-cycle)의 측정값 → 측정값을 나타내는 차수 5의 이동평균
- 5-MA : 연도 기준으로 기준 년도 + “앞으로 2년 뒤로 2년”
- 첫부분 2개의 5-MA와 끝부분 2개의 5-MA 값이 존재 X
→ 끝부분 근처의 추정값을 허용하는 더 정교한 추세-주기 추정 기법을 사용한다.
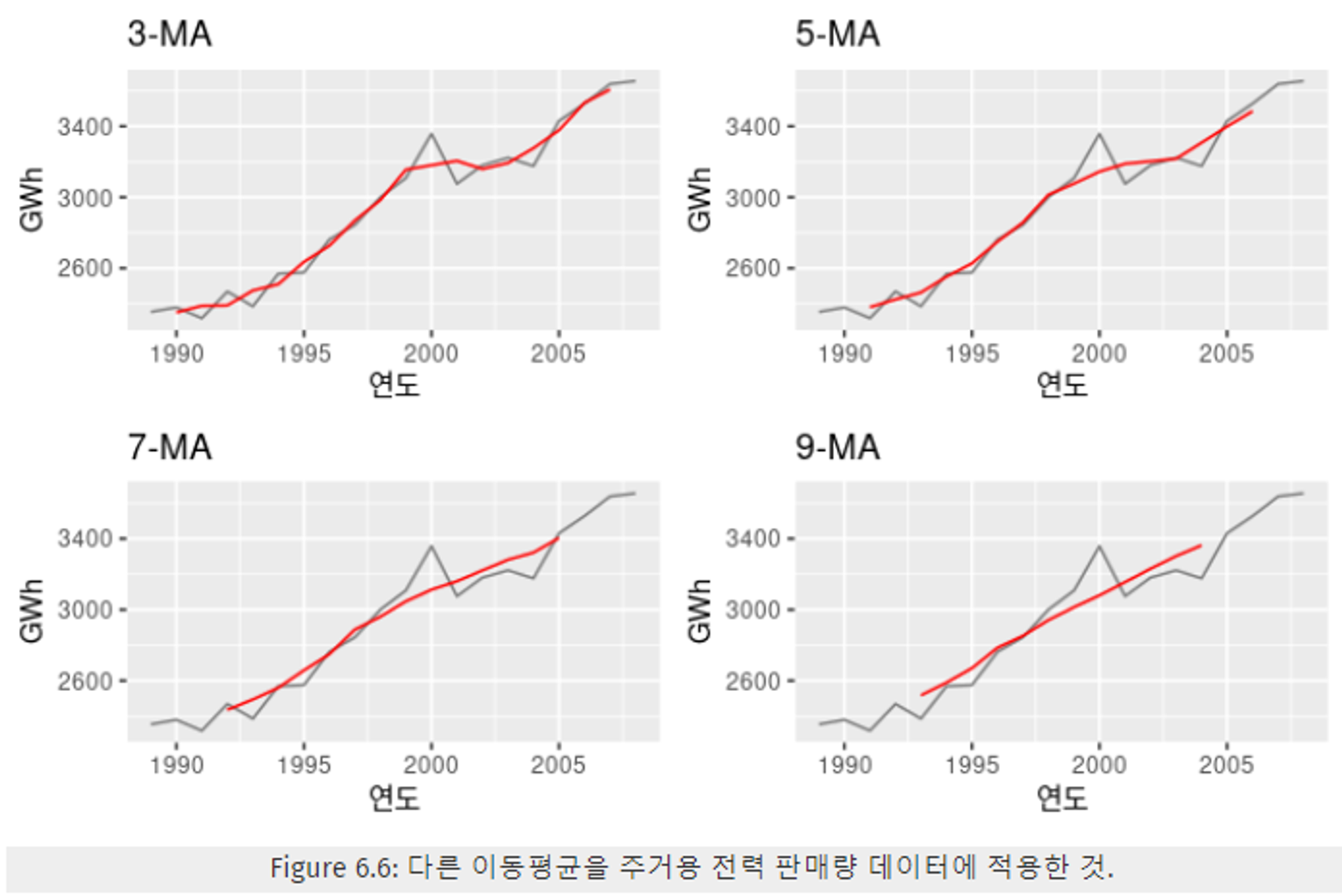
- 파악할 점
- 원본 데이터보다 얼마나 더 매끄러운지
- 부가적인 변동을 제외한 시계열의 주된 움직임
- 차수 → 추세-주기(trend cycle) 추정치의 매끄러운 정도를 결정한다.
- 클수록 더 매끄럽다.
- 주로 3, 5, 7 같은 홀수이다. (대칭)
6.2.2 이동평균의 이동평균
- 이동평균을 또 이동평균 한다.
- 짝수 차수 이동 평균을 대칭적으로 만들기 위함이다.
- 2×4 MA : 4-MA 한 뒤, 2-MA 진행
- 차수 4의 중심화된 이동평균 : 4-MA와 같은 짝수 차수 이동 평균 이후에 2-MA가 나올 때

- 짝수에 대한 이동 평균 시, 나올 수 있는 2가지 경우에 대한 평균을 진행한다.
- 관측치에 대한 가중 평균 형태이다.
- 대칭적이다.
- 다른 조합으로도 가능하지만, 대칭을 위해 짝수는 짝수끼리, 홀수는 홀수끼리
- 왜? 중심화된 이동평균을 사용하는가?
6.2.3 계절성 데이터에서 추세-주기를 측정하기
- 계절성 데이터에서 추세-주기(trend-cycle)을 측정하기 위해서
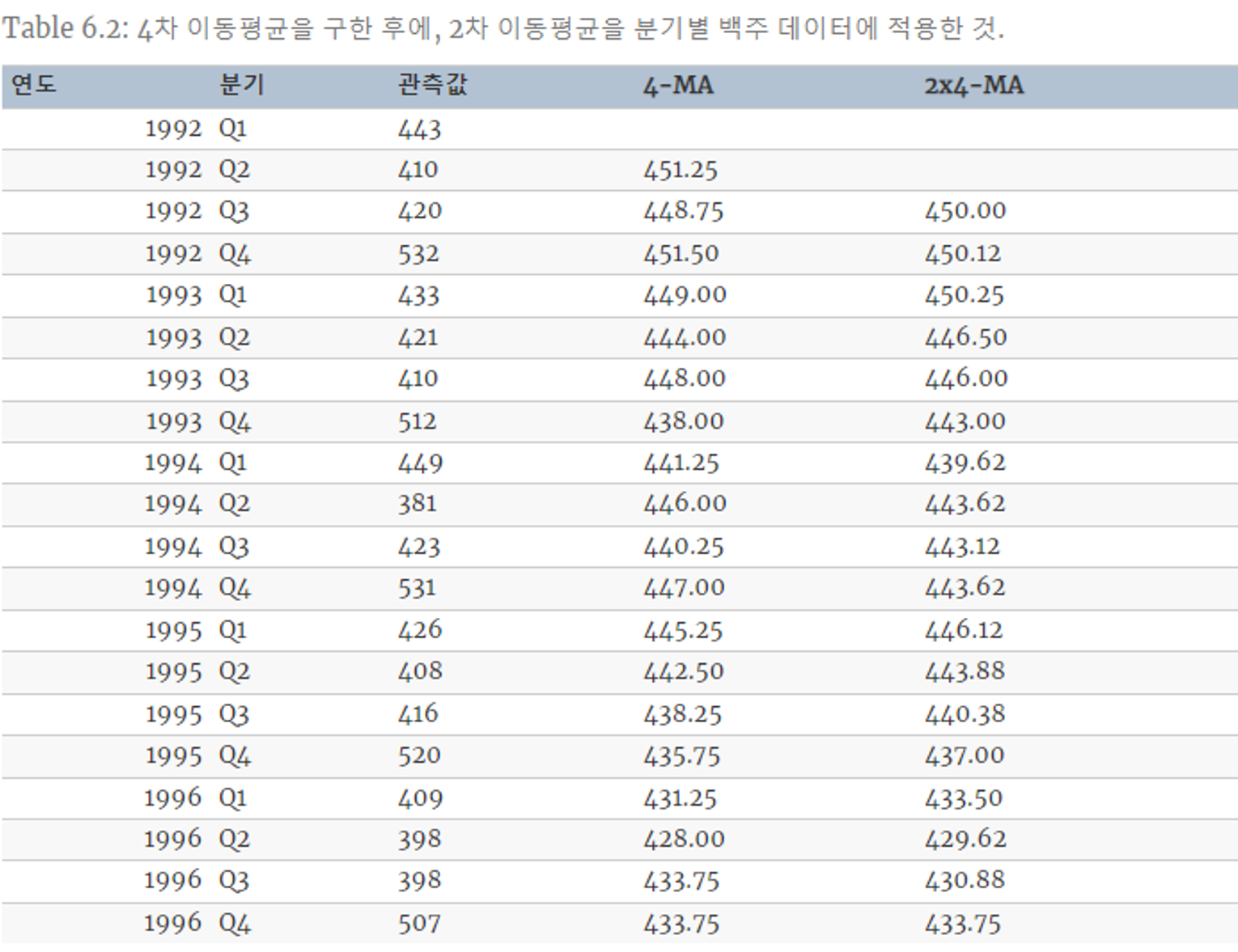
- 차수 4의 중심화된 이동평균(2×4 MA)
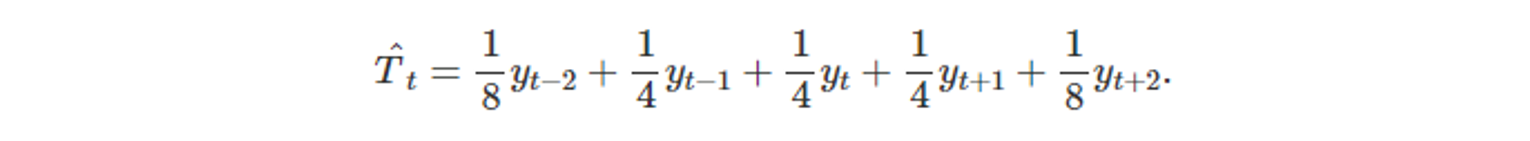
- 첫 번째와 마지막이 같은 가중치(1/8)을 가진다
→ 분기별 데이터로 봤을 때, 같은 분기에 같은 가중치가 주어진다
→ 평균으로 인해 계절성 변동이 사라진다.
→ 결과값 T_hat_t에 계절성 X
(2×8 MA 이나 2×12, 2×12 MA 를 사용해도 비슷한 결과이다.)
- 첫 번째와 마지막이 같은 가중치(1/8)을 가진다
- 일반화 2×m MA 일 때,
- 첫 번째와 마지막을 제외하고 모든 관측값에 1/m의 가중치를 가진다.
- 첫 번째와 마지막은 1/(2m)의 가중치를 가진다.
- 짝수의 계절성 주기를 가지는 시계열 데이터? (분기, 월 등)
- 2×m MA 를 사용하여, 추세-주기를 측정 (m이 짝수)
- 홀수의 계절성 주기를 가지는 시계열 데이터?
- m MA 를 사용하여, 추세-주기를 측정 (m이 홀수)
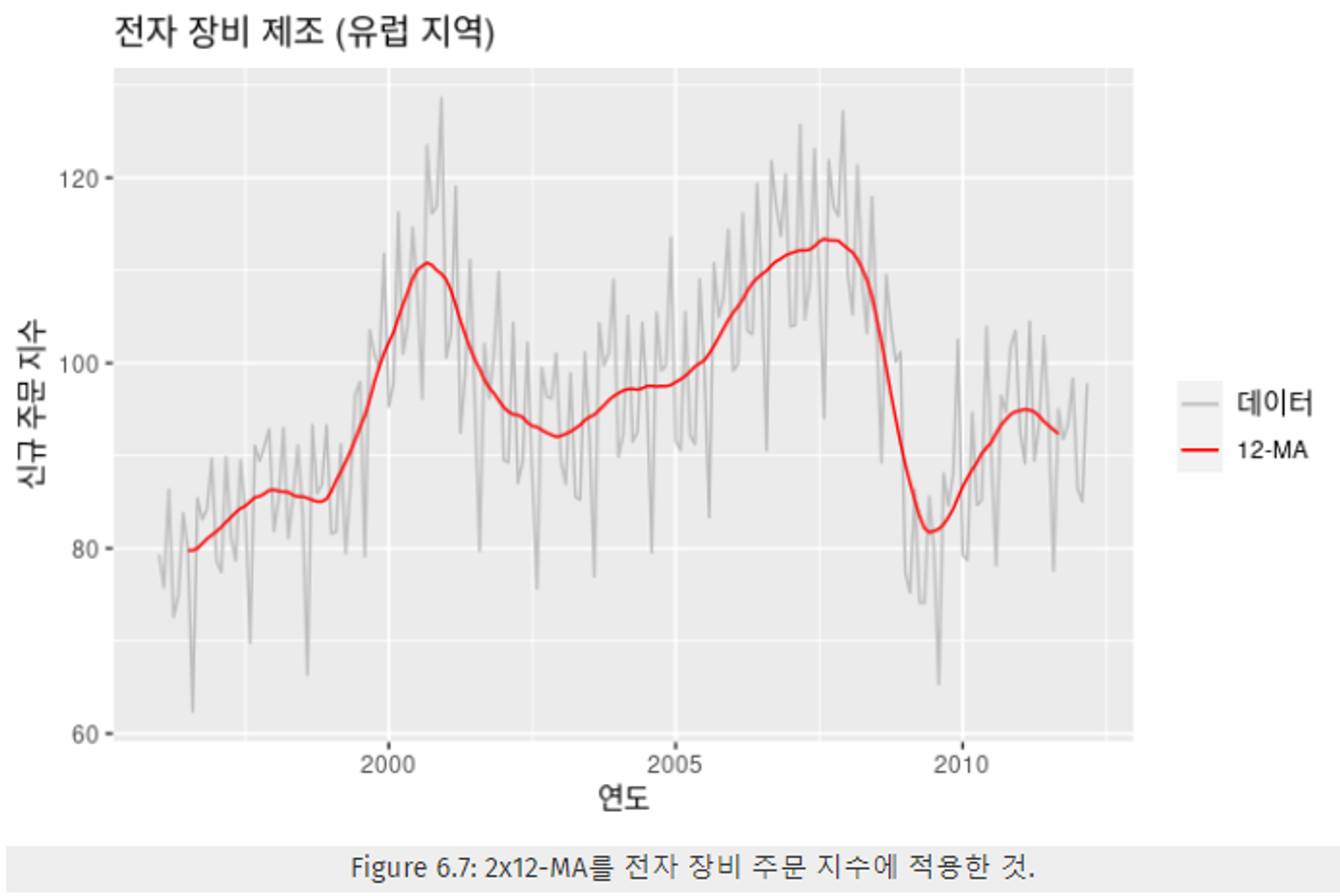
- 2×12 MA 를 적용한 결과, (월별 데이터이므로 m=12, → 짝수 → 2 x m MA 형태)
- 매끄러운 선에서 계절성이 제거됨.
- 만약 12, 24, 36 등 과 같은 값이 아닌 다른 값으로 했다면 계절성 변화를 나타내는 매끄러운 선일 것이다.
6.2.4 가중 이동평균
- 이동평균의 이동평균 ⇒ 가중 이동평균(가중치를 준 이동평균) 형태이다.
- 2×4 MA ⇒ 가중 5-MA
- 가중 m-MA (↔ 단순 m-MA)

- k = (m-1) / 2
- 가중치 : [a_-k, … , a_k]
- 모두 더하면 1
- aj = a-j (대칭적)
- 천천히 증가하다가 감소하는 가중치를 이용하여
매끄러운 추세-주기(trend-cycle)를 얻을 수 있다.
