온라인 Forecasting 교재 [Forecasting : Principles and Practice] 2장 3절을 참고하여 작성하였습니다.
2.3 시계열 패턴
- 시계열 패턴에 대한 정의는 크게 3가지 이다.
- 추세(trend), 계절성(seasonality), 주기성(cycle)
2.3.1 추세(trend)
- 증가하거나 감소하는 경향
- 선형적일 필요는 없으며, 증가하는 추세에서 감소하는 추세로 방향이 변화할 수 있다.
2.3.2 계절성(seasonality)
- 1년의 특정한 때 or 1주일에 특정한 요일과 같은 계절성 요인이 데이터에 영향을 주는 것
- 핵심은 단위 기간에 정기적으로 발생한다.
- 당뇨병 약의 월별 매출액은 연말에 발생하는 약품 가격 변동에 의해 계절성이 존재한다.
ㄟ(▔,▔)ㄏ 계절성 요인?
정의가 불명확하다고 생각하여 내 방식대로 정리하자면,
1년마다 정기적으로 반복되는 상황,
1주마다 정기적으로 반복되는 상황으로 인해 데이터에 영향을 준다면
그것이 계절성 요인이다. 라고 정의할 수 있을 것 같다.2.3.3 주기성(cycle)
- 특정 주기마다 증가하거나 감소하는 모습을 보이는데, 정해진 기간마다 발생하지 않는 것
- 핵심은 정기적이지 않다. (계절성과의 차이 존재)
Figure 2.3: 서로 다른 패턴을 나타내는 4가지 시계열 예제
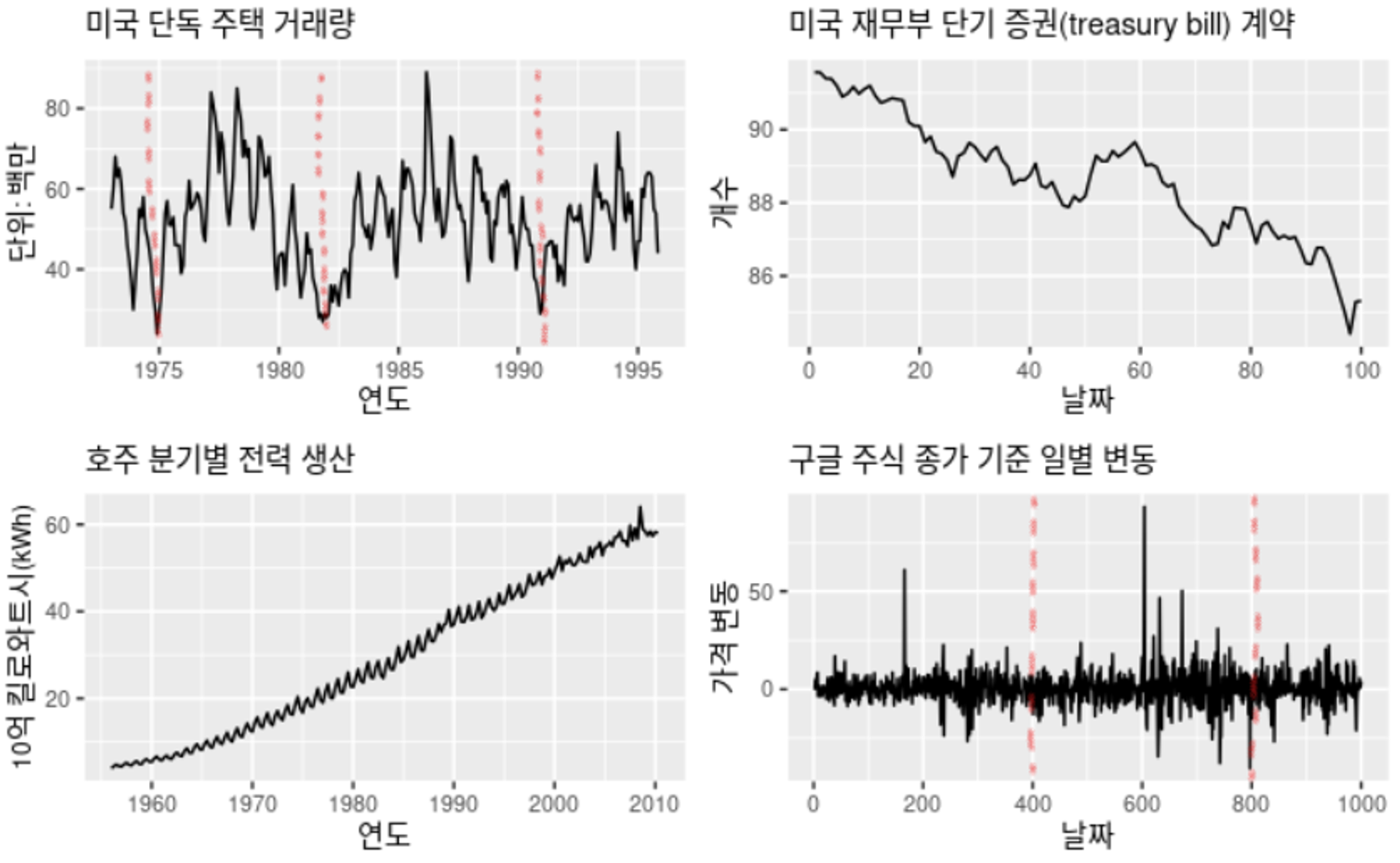
- 월별 미국 단독 주택 거래량
- 추세 X : 데이터를 전체적으로 보았을 때 분명한 추세가 없고 증가 감소를 반복한다.
- 계절성 O : 매년 강한 계절성을 보인다.
- 주기성 O : 빨간 점선을 보면 6~10년 간의 주기적인 패턴이 보인다. 이 때 이러한 패턴은 특정 기간마다 발생하지 않기 때문에 계절성이 아닌 주기성이 존재한다.
ㄟ(▔,▔)ㄏ 매년 강한 계절성을 보인다.
해당 그래프를 보고 어떻게 매년 계절성이 존재하는지 파악할 수 있는지?- 미국 재무부 단기 증권 계약
- 추세 O : 증가 감소를 반복하고 있지만 데이터를 전체적으로 보았을 때, 꾸준히 감소하는 추세를 보인다.
- 계절성 X : 특정 시점마다 정기적인 패턴이 보이지 않는다.
- 주기성 X : 주기마다 특징적인 패턴이 보이지 않는다.
ㄟ(▔,▔)ㄏ 주기성 X : 주기마다 특징적인 패턴이 보이지 않는다 ?
해당 내용은 교재를 참고하지 않고 적어본 내용인데, 교재 내용을 인용하면,
훨씬 더 긴 시계열 데이터가 있었더라면 보이는 “추세”가 하나의 “주기”가 될 수 있지만,
현재 데이터를 기준으로 보면 “추세”가 존재하고,
”주기”는 존재하지 않음을 알 수 있다.- 호주 분기별 전력 생산
- 추세 O : 증가 감소를 반복하고 있지만 데이터를 전체적으로 보았을 때, 꾸준히 증가하는 추세를 보인다.
- 계절성 O : 그래프를 보면 증가 감소하는 방향이 일정 간격마다 변화하는 것으로 보인다. 그렇기 때문에 이를 정기적인 패턴으로 보고 계절성이 존재한다고 볼 수 있다.
- 주기성 X : 주기적인 행동이 보이지는 않는다.
ㄟ(▔,▔)ㄏ 주기성 X : 주기적인 행동이 보이지는 않는다. ?
교재의 내용을 보면서,
아직 계절성과 주기성에 대한 개념이 잡혀있지 않아 그렇게 생각했을 수도 있지만,
계절성과 주기성은 서로 동시에 존재할 수 없는 특성들인가? 에 대한 궁금증이 생겼다.
내가 이해한 개념
- 계절성 : 특정 시점(연말, 0월 0일, 월말마다)에 정기적으로
시계열 데이터에 영향을 주는 요인이 존재할 때,
- 주기성 : 특정 시점이 아닌 어느정도의 주기마다(?) 솔직히 그래프의 모양?이
어느정도 두루뭉술한 기간마다 반복적인 패턴을 보인다? 하면
주기성이 존재한다고 이해했다.- 구글 주식 종가 기준 일별 변동
- 추세 X : 데이터 전체적으로 보았을 때, 아무런 추세가 보이지 않는다.
- 계절성 X : 특정 시점마다 정기적인 패턴이 보이지 않는다.
- 주기성 X : 200 시점과 600 시점에서 값이 유독 튀는 것을 볼 수 있다. 이는 뒤에 더욱 긴 시계열 데이터를 확인해봐야 알겠지만, 현재 데이터만으로 보면 주기성이 존재한다고 할 수 없을 것 같다.
ㄟ(▔,▔)ㄏ 200 시점과 600 시점에서 값이 유독 튀는 것을 볼 수 있다. ?
미국 단독 주택 거래량 데이터는 주기성이 존재한다고 설명한다.
결국 일정 주기 동안 그래프의 모양이 비슷하면 주기성이 존재한다고 이해하였다.
구글 주식 종가 기준 일별 변동 데이터는 주기성이 존재하지 않는다고 설명한다.
400~450 정도 단위의 주기가 존재한다고 가정한다면,
1000 시점 부근의 값이 튈 수도 있음을 예측할 수 있다고 생각하는데
(물론 더 긴 시계열 데이터가 존재해야 겠지만)
해당 데이터는 주기성이 존재하지 않는다고 할 수 있는지에 대해서 궁금하다.