온라인 Forecasting 교재 [Forecasting : Principles and Practice] 2장 6절을 참고하여 작성하였습니다.
2.6 산점도
- 산포도, Scatterplots, 흩뿌림 그래프
- 산점도로 표현할 수 있는 이유는 “시점”이라는 두 데이터의 공통된 특성이 있기 때문에, 두 가지 데이터가 가지는 각기 다른 특성들을 한 번에 표현할 수 있다.
- 산점도의 필요성
- 변수 사이의 관계를 시각화 하는데 유용하다.
- Figure 2.7은 전력 수요에 대한 시계열 데이터와, 기온에 대한 시계열 데이터인데, 두 그래프를 보면 그래프의 경향을 보며 관계를 파악할 순 있지만, 어렵고 부족하다.
- Figure 2.8을 보면 시점이 겹치는 값에 대해 두개의 데이터를 평면에 표현할 수 있고, 이를 산점도라고 한다. 산점도를 보면 전체적인 경향이 비례적임을 알 수 있다. (온도가 올라가면 에어컨 사용량으로 전력 수요 증가)
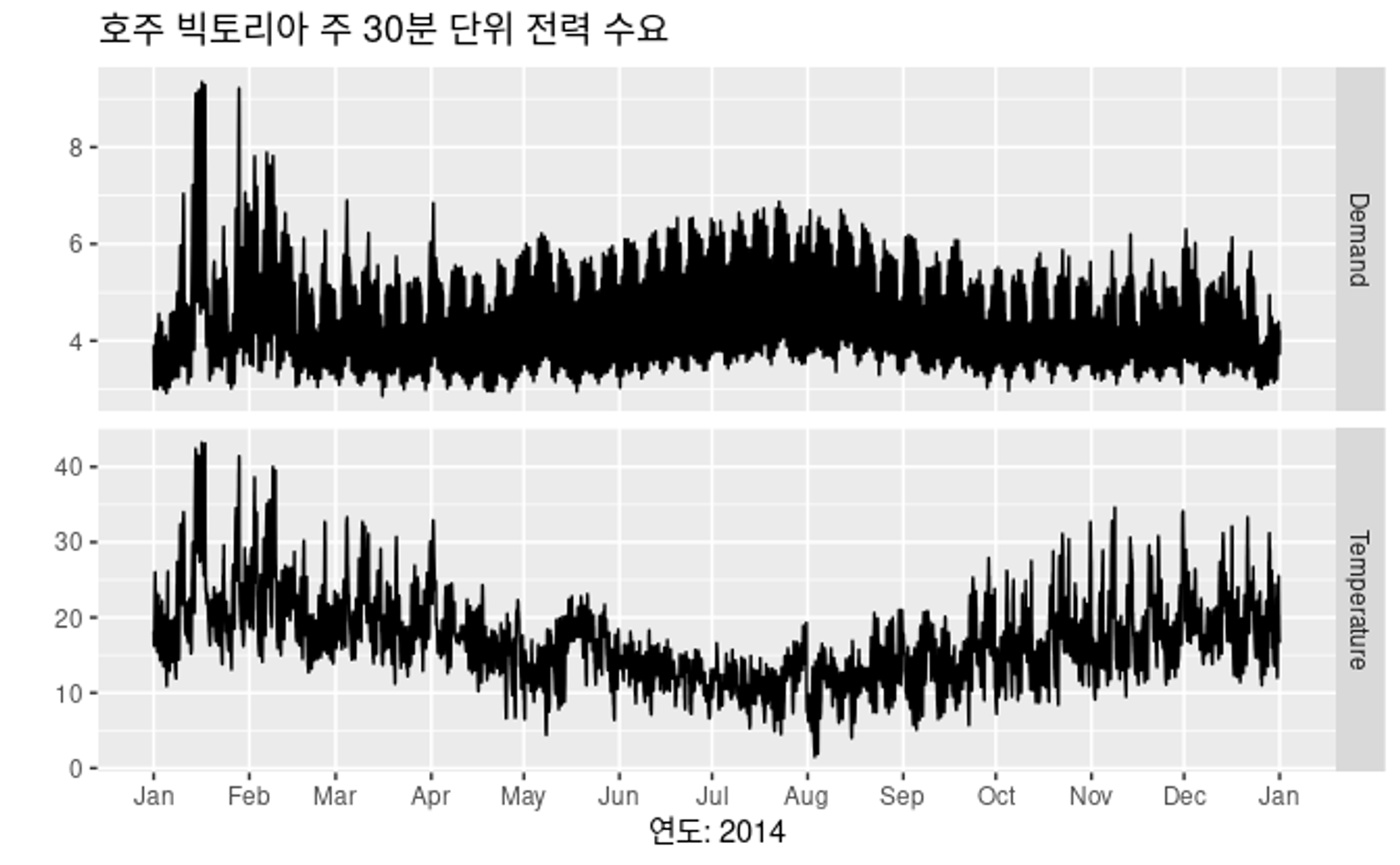
Figure 2.7: 2014년 호주 빅토리아 주 30분 단위 전력 수요와 기온 (위 : 전력수요, 아래 : 기온)
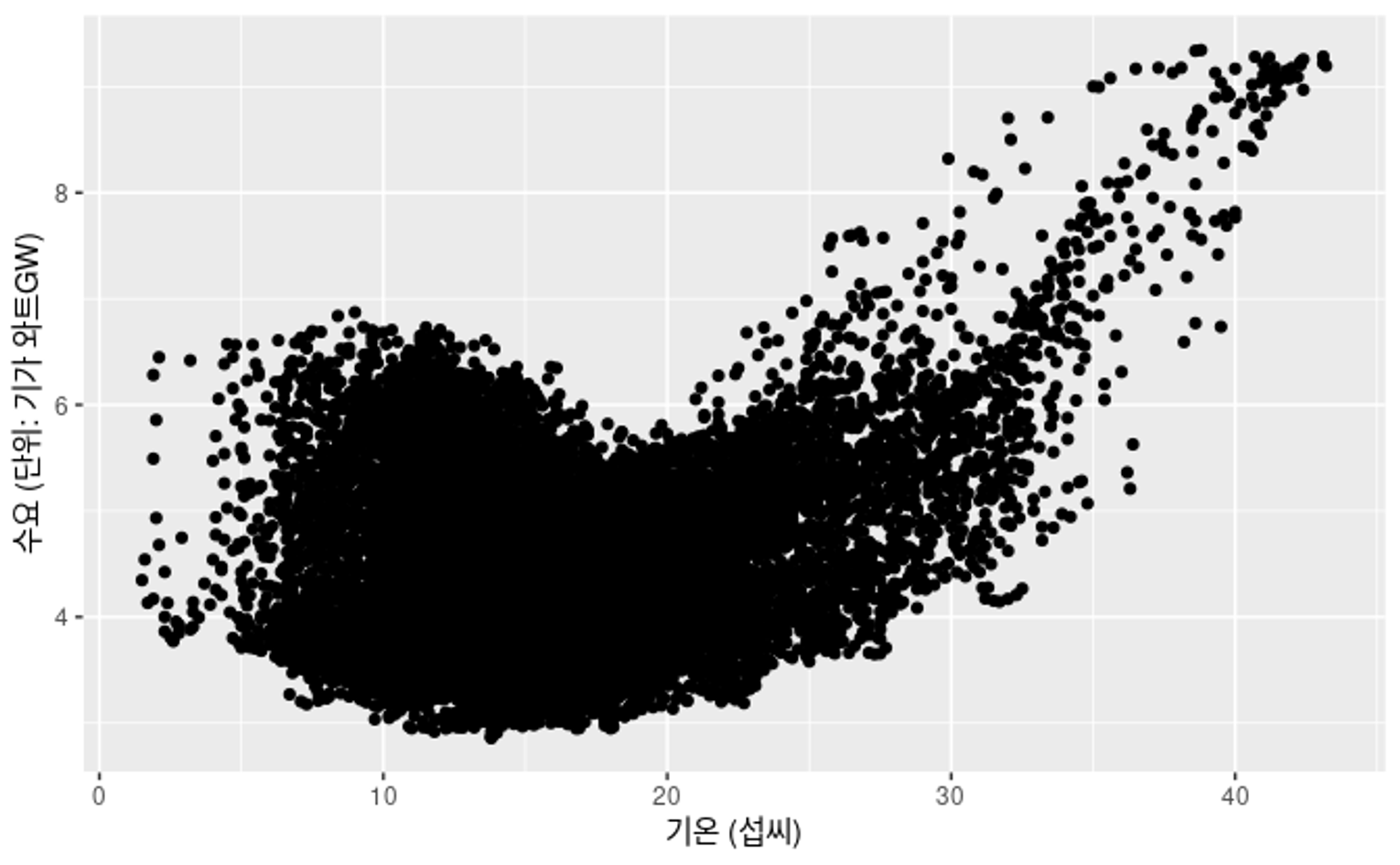
Figure 2.8: 2014년 호주 빅토리아 주의 30분 단위 전력 수요를 기온에 따라 나타낸 그래프
ㄟ(▔,▔)ㄏ
해당 산점도에서 기온이 낮을 때, 전력 수요가 적은 것을 확인할 수 있는데,
유독 이 부분(왼쪽 아래)에 데이터가 몰려있는 것을 알 수 있다.
이러한 형태가 의미하는 바가 무엇인지?
스스로 생각했을 때는
전체 시계열 데이터로 봤을 때,
호주 빅토리아 주의 날씨가 주로 5~25도 사이에 몰려있기 때문이 아닐까..2.6.1 상관
- 상관계수(correalation coefficient)
- 두 변수 사이의 관계의 강도를 측정할 때 사용하는 값

- 상관계수 r 은 -1 ~ 1 사이의 값을 가지며,
- 부호는 양/음의 관계, 절댓값의 크기는 강한/약한 관계 정도를 나타낸다.
- 아래 Figure 2.9를 통해 상관관계에 대한 감을 익힐 수 있다.
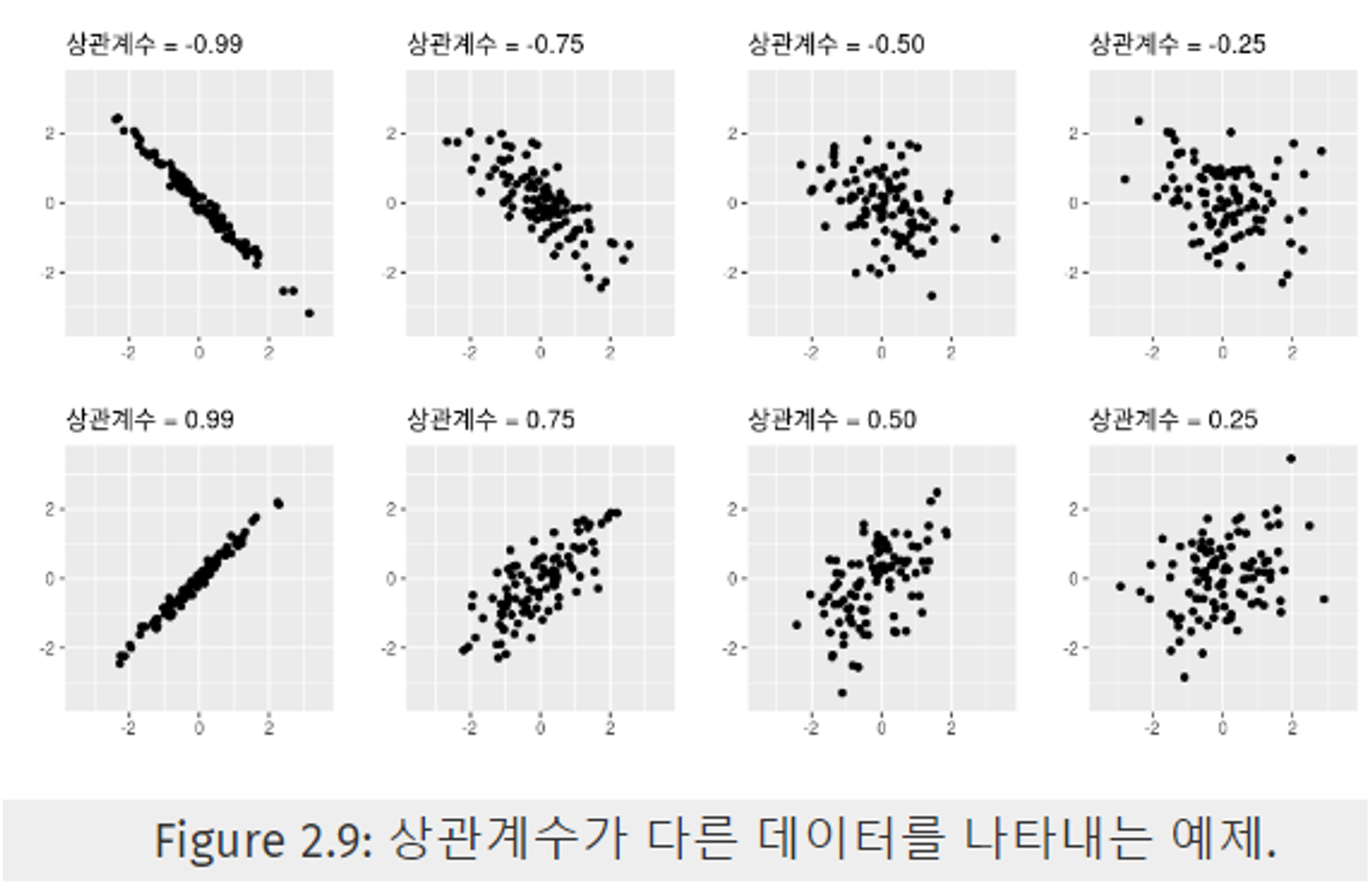
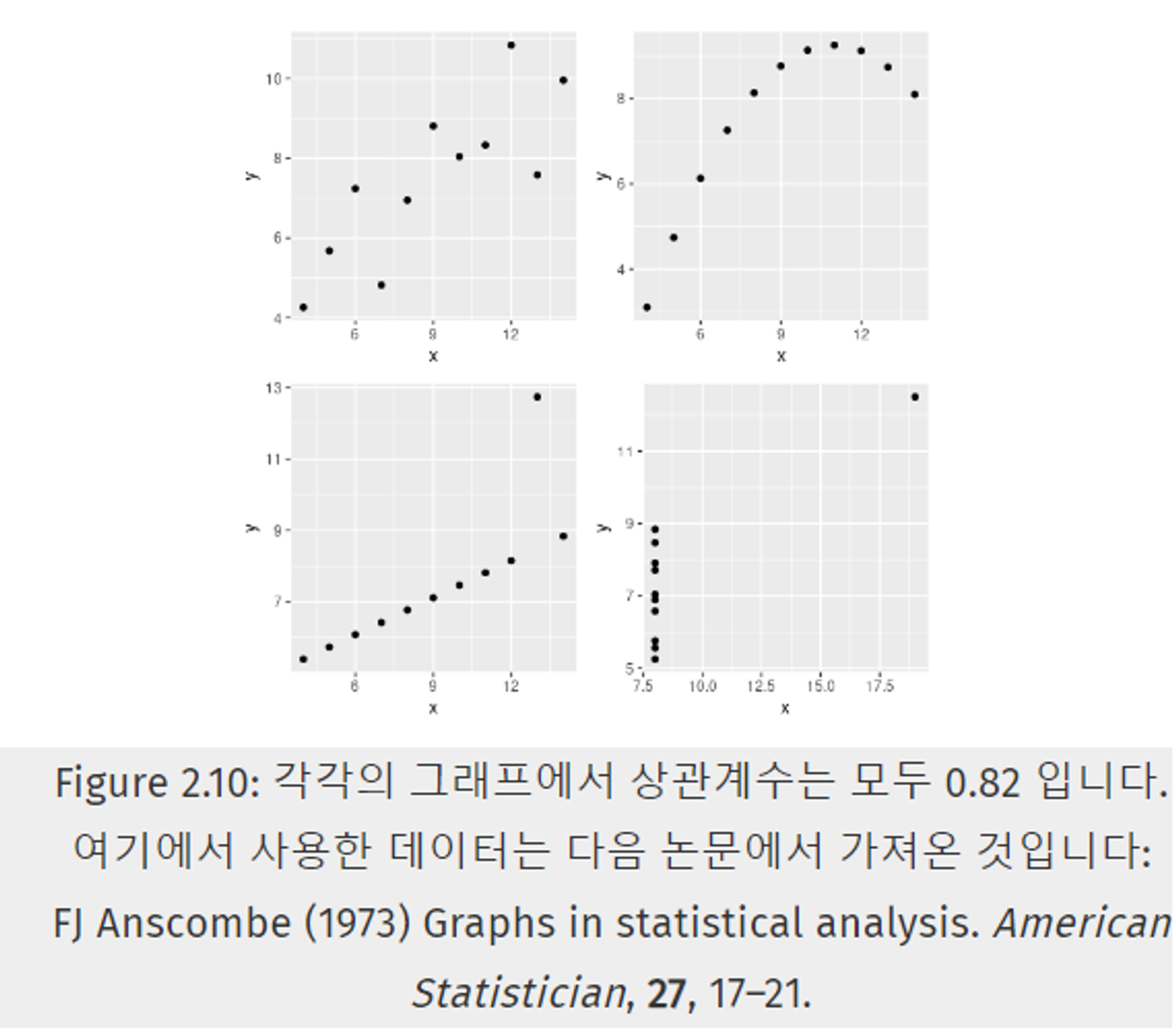
- 아래 Figure 2.10에 보이는 4개의 그래프는 모두 0.82의 상관계수를 가진다.
- 상관계수를 참고하여 변수간 관계를 파악하는 것은 맞지만, 그에 너무 의존하면 안된다는 것을 알 수 있다.
2.6.2 산점도 행렬
- 예측 변수를 다른 예측 변수를 통해 표현하는 것이 그 사이의 관계성을 파악하는 데 도움이 된다.
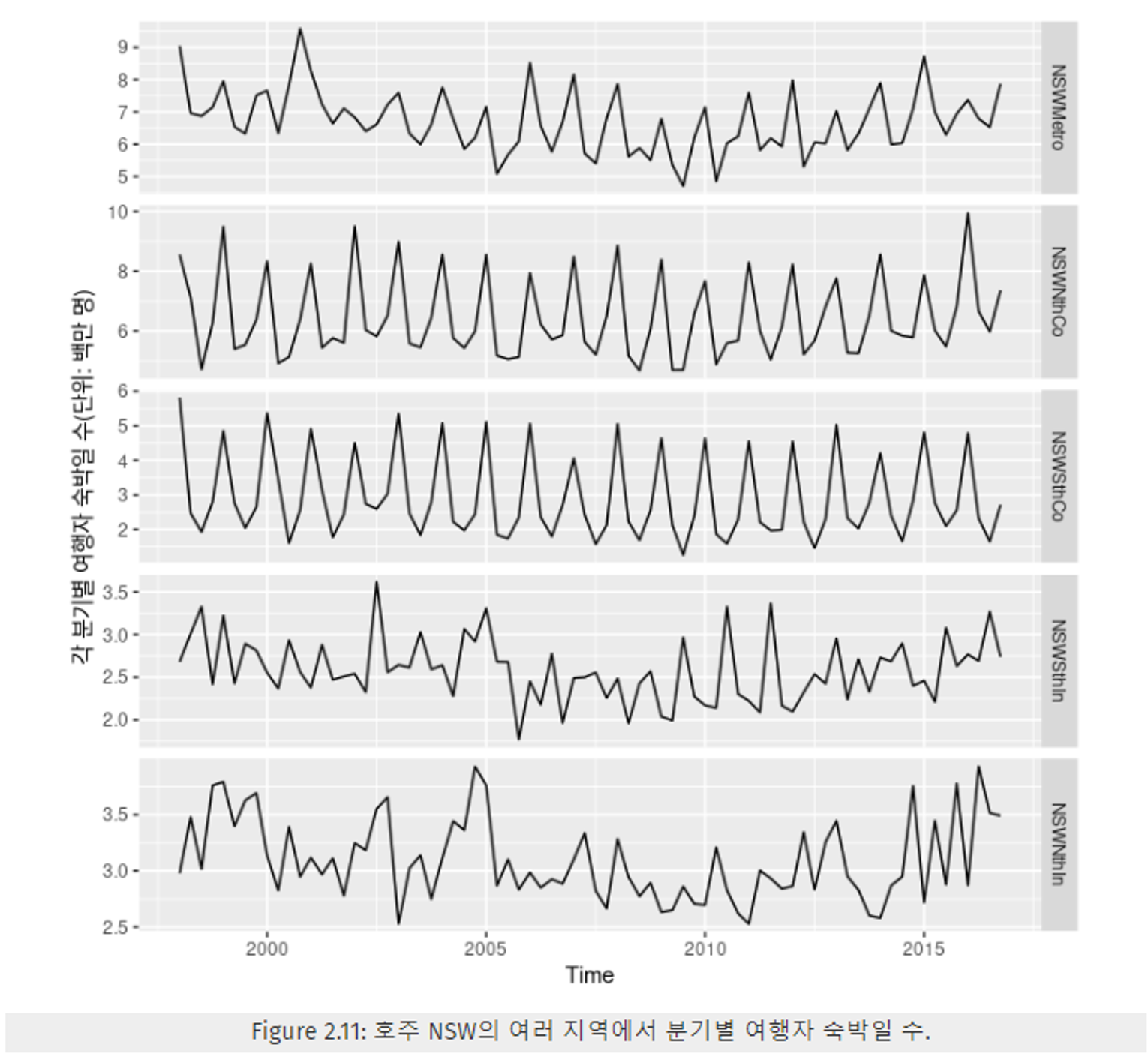
- 아래 Figure 2.11은 각 지역의 여행자 숙박일 수를 각각의 그래프로 표현한 것이다.
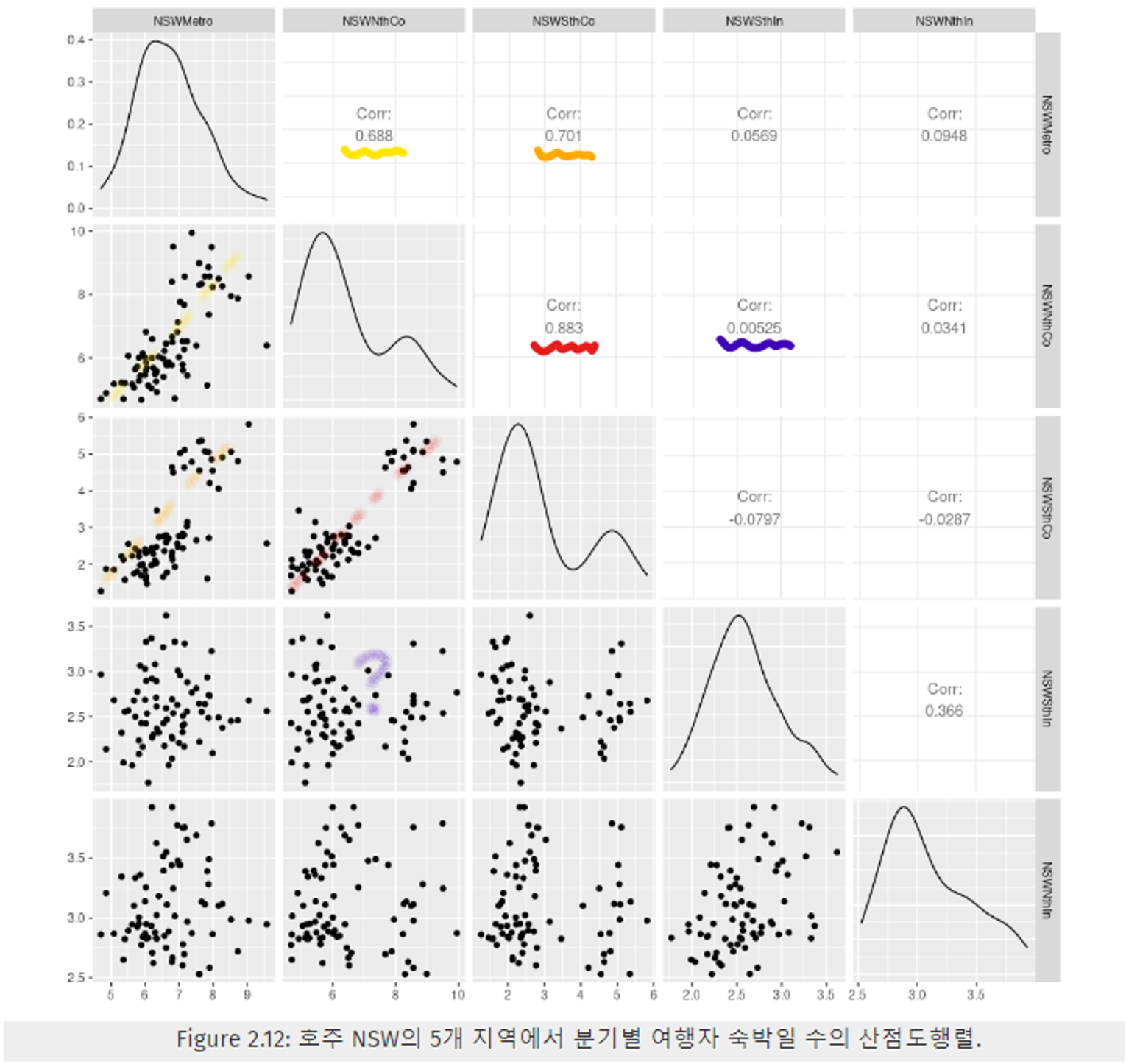
- 아래 Figure 2.12는 A 지역의 여행자 숙박일 수에 따른 B 지역의 여행자 숙박일 수와 같이 서로 지역간 여행자 숙박일 수에 대한 관계를 파악할 수 있다.
- 우측 상단 부분에는 각 데이터 간 상관 관계를, 대각 성분은 해당 데이터의 밀도를, 좌측 하단 부분에는 두 데이터를 시점 단위로 결합한 산점도를 표현하였다.
- 빨간 색으로 표시한 값이 가장 높은 상관관계(0.883)를 가지며, 해당 산점도를 보아도 비례적인 경향을 보임을 알 수 있다. (실제로 둘다 해안 방문 객을 의미 - NSW 북쪽 해안 방문객과 NSW 남쪽 해안 방문객)
- 남색으로 표시한 값이 가장 낮은 상관관계(0.00525)를 가지며, 해당 산점도를 보아도 아무런 경향이 없음을 알 수 있다.
- 여기서 주목할 점은 실제로 Figure 2.11의 두 번째, 세 번째 데이터를 보면, 데이터의 계절성이 존재함을 알 수 있고, 이 두개의 상관관계가 가장 높게 나왔음을 알 수 있다.
- 또한, 네 번째, 다섯 번째 그래프에는 어떠한 시계열 데이터의 특성이 존재하지 않고, 해당 데이터와 계절성이 존재하는 데이터의 상관관계를 보면 대체로 낮은 값임을 알 수 있다.
- 여기서 재밌는 것은 시계열 데이터의 특성이 존재하지 않는 네 번째, 다섯 번째 데이터 끼리의 상관관계가 더 높다는 점이다.