
온라인 Forecasting 교재 [Forecasting : Principles and Practice] 7장 5절을 참고하여 작성하였습니다.
7.5 지수 평활에 대한 혁신 상태 공간 모델
- 지수 평활 기법에 깔린 통계 모델에 대한 설명
- 통계 모델 : 전체 예측분포를 만들어줄 수 있는 무작위적 데이터 생성 과정
- 같은 점의 예측값을 내는 동시에 예측 구간도 생성한다.
- 각 모델은 측정식과 몇 가지 상태식으로 구성된다. (상태 공간 모델 이라고도 함.)
- 측정식(measurement equation) : 관측된 데이터를 묘사하는 식
- 상태식(state equation) : 아직 관측되지 않은 성분이나 상태(수준, 추세, 계절성)
- 각 지수 평활 기법마다 두 가지 모델이 존재한다.
- 덧셈 오차
- 곱셈 오차
- 평활 매개변수 α 가 같다면, 오차 방식과 관계없이 모델의 예측값은 동일하다.
- 하지만, 다른 예측 구간을 생성한다.
- ETS(오차 Error, 추세 Trend, 계절성 Seasonal)
- 덧셈 오차와 곱셈 오차까지 분류 기준에 추가하기 위해 Table 7.5 에 오차 Error를 추가한다. (3차원 형태의 표로 생각하면 된다.)
- 오차 ={A, M}, 추세 ={N,A,Ad}, 계절성 ={N,A,M} A : 덧셈, M : 곱셈 / N : 없음, A : 덧셈, Ad : 덧셈 감쇠 / N : 없음, A : 덧셈, M : 곱셈
7.5.1 ETS(A, N, N) : 덧셈 오차를 이용하는 단순 지수평활
-
덧셈 오차, 추세 없음, 계절성 없음
-
단순 지수 평활의 성분 형태 (오차 없이)
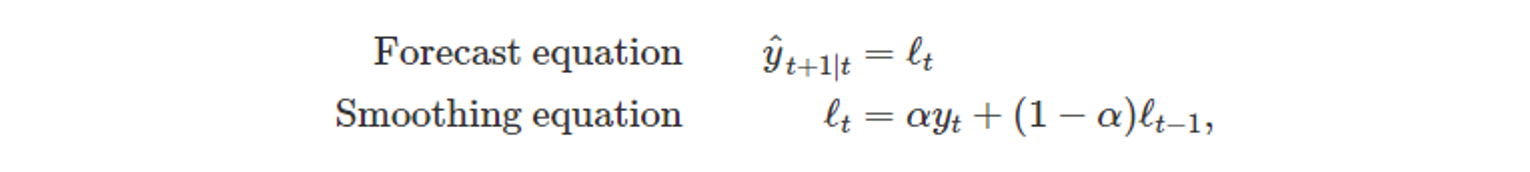
-
Smoothing equation에 대한 정리하면,
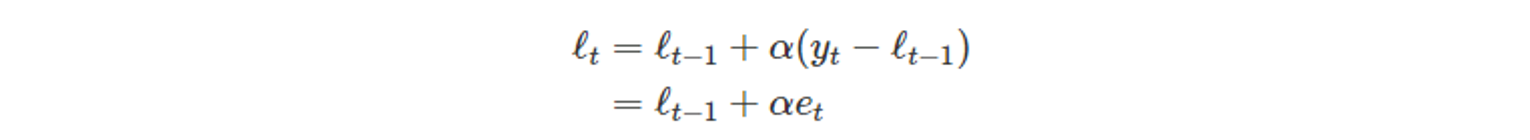
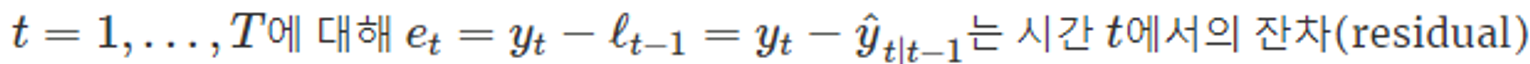
오차 보정 (error correction)에 대한 식을 얻을 수 있다.
-
시간 t에서 오차가 음수?
- y_t < y_hat_t|t-1 → 시간 t-1에서의 추정 값이 과도하다. → 하향 조정 필요 → 하향 조정된 이전 수준값 ℓ_t-1
-
평활 매개변수 α에 따라 조정값의 크기가 달라진다. (α가 1에 가까울수록 큰 조정)
-
t에서의 관측값 = t-1 에서의 수준값 + t에서의 오차 를 나타내기 위해
(y_t = ℓ_t−1 + e_t) 와 같은 식으로 표현할 수 있다.
- 이 때, 오차 e_t를 innovation state space model로 만들기 위해
e_t에 대한 확률분포 식을 구체적으로 적어야 한다. -
e_t에 대한 확률분포 식
- e_t = ε_t ∼ NID(0, σ^2)
- 평균이 0이면서, 분산이 σ^2 인 정규 분포를 따르는 형태 → 백색 잡음
- NID : Normally and Independently Distributed (정규적이고 독립적인 분포)
- e_t = ε_t ∼ NID(0, σ^2)
-
ETS(A, N, N) 상태공간모델의 식
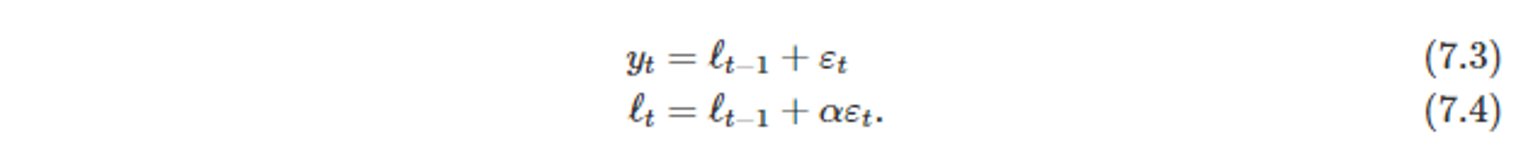
-
오차의 통계적인 분포를 함께 이용하여 e_t를 ε_t로 표현할 수 있다.
-
단순 지수 평활을 이루는 innovations state space model이 된다.
-
식 7.3 측정 방정식
- 관측값 y_t과 아직 관측되지 않은 상태(state)와의 관계
- 관측값 y_t는 아래 3가지 부분을 활용한 선형 함수
- 수준 ℓ_t−1
- y_t의 예측 가능한 부분
- 오차 ε_t, y_t의 예측 가능하지 않은 부분
-
식 7.4 상태 방정식
- 시간에 따른 상태(state)의 변화
- 높은 α 값은 급격한 수준 변화, 작은 α 값은 매끄러운 변화
-
7.5.2 ETS(M,N,N): 곱셈 오차를 이용하는 단순 지수평활
- ETS(M, N, N) 상태공간모델의 식
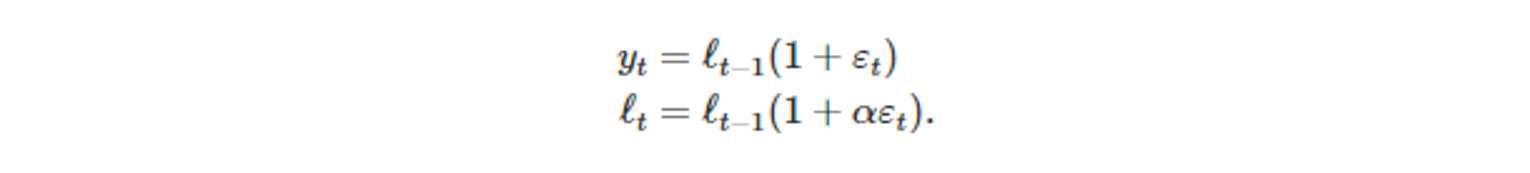
- 한 단계 앞 학습 오차 → 상대적인 학습 오차를 통해 곱셈 오차를 이용
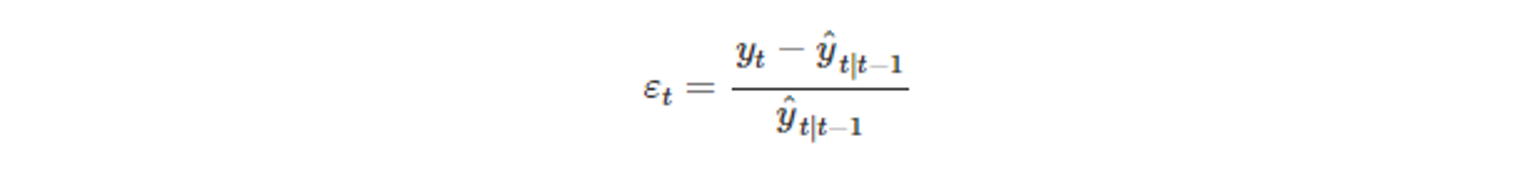
- 오차는 실제값 - 예측값을 예측값으로 나눈 값
- ε_t ∼ NID(0, σ^2)
- 아래 식을 활용하여 e_t에 대한 식을 산출할 수 있다.
- y_hat_t|t−1 = ℓ_t−1
- y_t = ℓ_t−1 + ℓ_t−1 ε_t*
- e_t = y_t − y_hat_t|t−1 = ℓ_t−1 ε_t*
7.5.3 ETS(A,A,N): 덧셈 오차를 이용한 홀트의 선형 기법
- ETS(A,A,N) 상태공간모델의 식
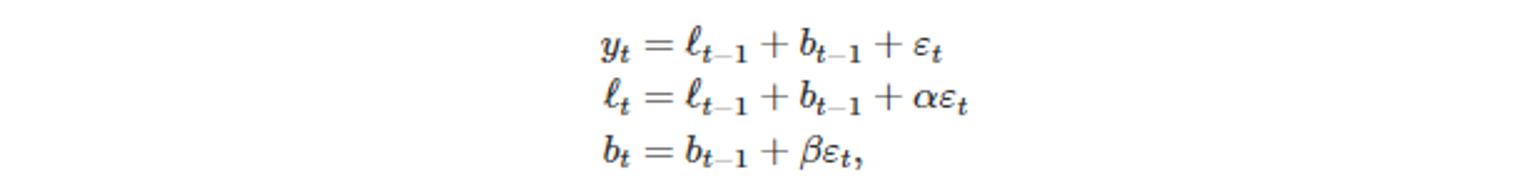
- 한 단계 앞 학습 오차 ε_t
- ε_t = y_t − (ℓ_t−1 + b_t−1) ∼ NID(0,σ^2)
- 이러한 식에 Holt의 선형 기법에 대한 오차 보정식을 대입
- β = *αβ** 로 표현
- 한 단계 앞 학습 오차 ε_t
7.5.4 ETS(M,A,N): 곱셈 오차를 이용하는 홀트의 선형 기법
- ETS(M,A,N) 상태공간모델의 식
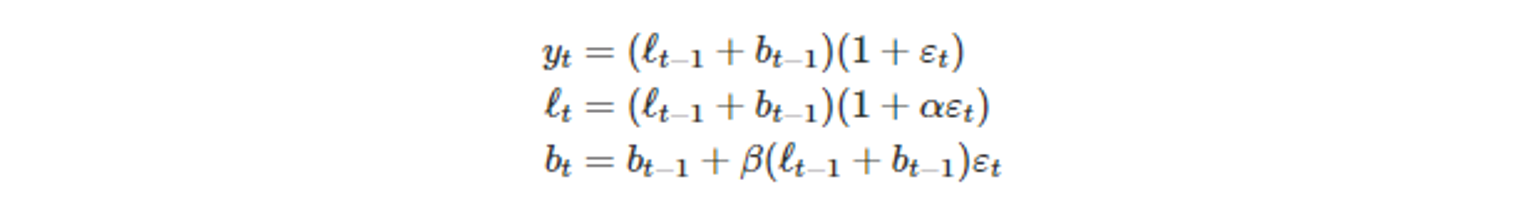
- 한 단계 앞 학습 오차 ε_t
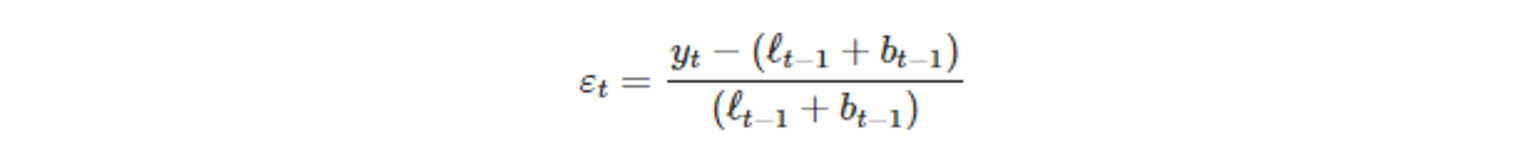
- 한 단계 앞 학습 오차 ε_t
7.5.5 다른 ETS 모델

