[Time Series] 추정과 모델 선택

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 7장 6절을 참고하여 작성하였습니다.

7.6 추정과 모델 선택

7.6.1 ETS 모델 추정

• 매개변수를 추정하는 방법
  • 기존 : 제곱 오차의 합 최소화
  • 대안 : 가능도(likelihood) 최대화
• 가능도(likelihood) ?
  • 특정한 모델에서 일어나는 데이터의 확률
• 가능도가 클수록 모델이 좋다.
  • 덧셈 오차 모델의 경우,
    • 가능도를 최대화하는 것과 제곱 오차의 합을 최소화하는 것과 같다.
  • 곱셈 오차 모델의 경우,
    • 가능도를 최대화하는 것과 제곱 오차의 합을 최소화하는 것과 다르다.
• 가능도를 최대화하여 아래 두 가지에 대해 구한다.
  • 평활 매개변수 α, β, γ, ϕ
    • 통상적으로 0부터 1사이의 값을 가진다.
    • 상태 공간 모델의 경우, *β=αβ**와 *γ=(1−α)γ**로 둔다.
    • 0<α<1, 0<β<α, 0<γ<1−α, 0.8<ϕ<0.98
  • 초기 상태 ℓ0, b_0, s_0, s−1, … , s_−m+1
• 허용성(admissibility) 제한 조건?
  • 전통적인 제한 조건의 범위보단 널널하다.
  • 예시로 ETS(A,N,N) 모델의 경우에는,
    • 전통적인 매개변수 범위는 0<α<1
    • 허용 범위는 0<α<2
  • 예시로 ETS(A,A,N) 모델의 경우에는
    • 전통적인 매개변수 범위는 0<α<1 와 0<β<α
    • 허용 범위는 0<α<2 와  0<β<4−2α

7.6.2 모델 선택

• 정보 기준(AIC, AIC_c, BIC,)를 사용하여 모델을 선택한다. (ETS 통계의 장점)
• AIC
  
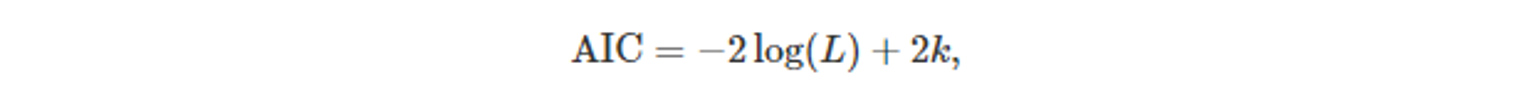
  • L : 모델의 가능도(Likelihood)
  • k : 잔차 분산을 포함하는 추정된 매개변수 개수 + 초기 상태값의 개수
• AIC_c
  
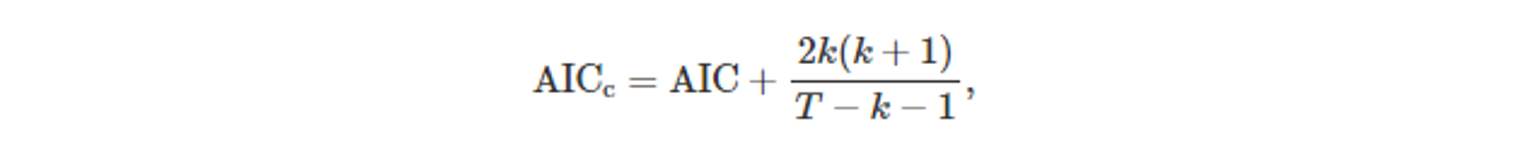
  • 작은 표본 크기에 보정된 AIC
• BIC
  
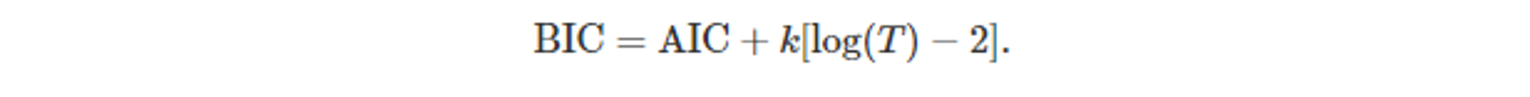
• 불안정성을 가지는 모델은 수치적으로 판단하기 어려울 수 있고, 이러한 모델에선 해당 척도를 고려하지 않는다.
  • ETS(A,N,M), ETS(A,A,M), ETS(A,Ad, M) → 오차는 덧셈오차, 계절성은 곱셈
  • Why? 상태 식에서 0에 가까운 값으로 나눌 수 있기 때문에
• 곱셈 오차는 데이터가 0이나 음수 값에 있으면 수치적으로 안정적이지가 않다.